Opgave magnetische keten / transformator – oefening 1

Opgave magnetische keten / transformator – oefening 1
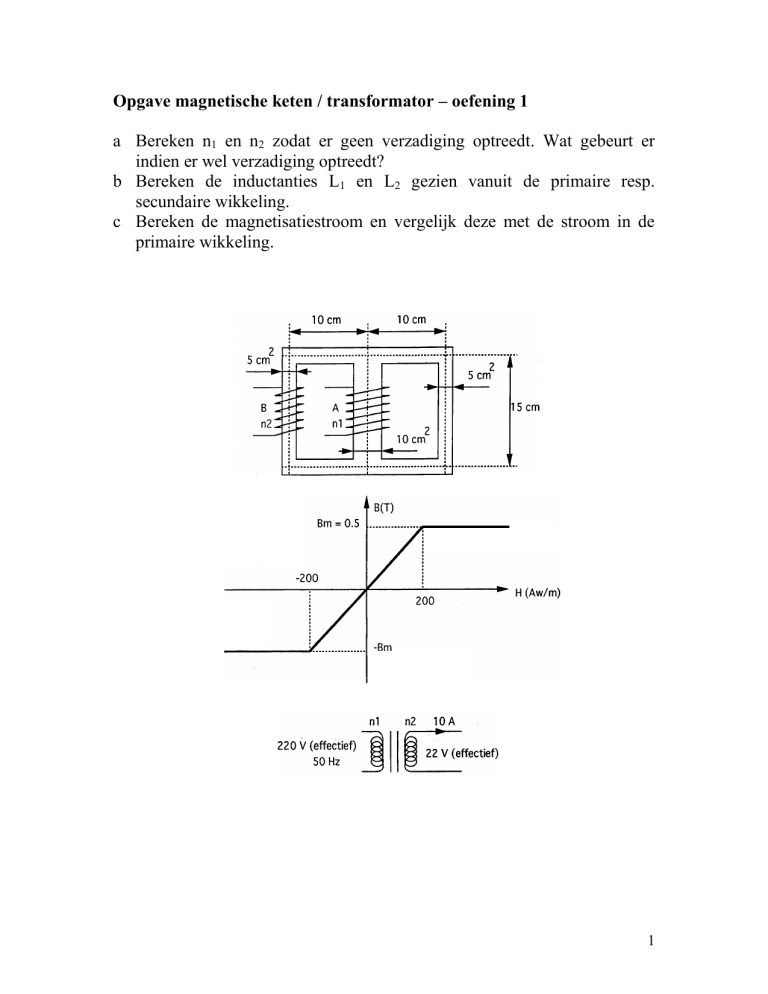
a Bereken n1 en n2 zodat er geen verzadiging optreedt. Wat gebeurt er
indien er wel verzadiging optreedt?
b Bereken de inductanties L1 en L2 gezien vanuit de primaire resp.
secundaire wikkeling.
c Bereken de magnetisatiestroom en vergelijk deze met de stroom in de
primaire wikkeling.
1
Uitwerking magnetische keten / transformator – oefening 1
a Bereken n1 en n2 zodat er geen verzadiging optreedt. Wat gebeurt er
indien er wel verzadiging optreedt?
 Er geldt voor de electro motorische kracht (e.m.k.)
en
d
dt
Ea  cos(t )  n

d
dt
en
e  E a  cos(t )

Ea
d
cos(t ) 
n
dt
2  E eff
Ea
sin( t ) 
sin( t )   a sin( t )
n 
n  2f
 Geen verzadiging wil zeggen dat de flux a kleiner moet zijn dan de
maximale flux max:
a  max

2  E eff
n  2f
 Bmax  A
 De maximale flux voor tak A en B is:
 max A  Bmax  AA  0.5  (10  10 4 )  5  10 4 Wb
 max B  Bmax  AB  0.5  (5  10 4 )  2.5  10 4 Wb
 Het aantal wikkelingen in de primaire tak n1:
n1 
2  Eeff
max A  2f

 Kies n1=2000 windingen
n1 
220 2
 1980.7
2  50  (5  10 4 )
3
2
 1  2  3  0
1  2  3

1
 Wegens de symmetrie in de transformator geldt:
 2  3
en
2  0.5  1
 Er geldt voor de verhouding tussen de e.m.k. waarden e1 en e2:
d
d
n1 1
n1 1
e1
n
dt 
dt

2 1
e2 n d 2 n d (0.5  1 )
n2
2
2
dt
dt
2
e1 220 2 2  2000


e2
n2
22 2

n2  400
 Ter controle:
a 2 
Eeff 2
2  f  n2

22 2
 2.48  10 4   max B
2  50  400
 In het geval van verzadiging treden er grote piekstromen op. Deze
geven aanleiding tot verliezen.
b Bereken de inductanties L1 en L2 gezien vanuit de primaire resp.
secundaire wikkeling.
 Voor de inductantie geldt:
L
n2
R
 Bereken nu eerst de weerstanden RA en RB:
RA 
RB 
lA
15  10 2
Aw

 6  10 4
  AA  1 
Wb
4

  10  10 
 400 
RA
RB
RB
F=n1i1
+
-
lB
35  10 2
Aw

 28  10 4
  AB  1 
Wb
4

  5  10 
 400 
 Weerstand R1 is de weerstand gezien vanaf de primaire kant:
R1  R A  RB // RB  R A 
RB  RB
Aw
 2  105
RB  RB
Wb
 Weerstand R2 is de weerstand gezien vanaf de secundaire kant:
R2  RB  R A // RB  RB 
R A  RB
Aw
 33  10 4
R A  RB
Wb
 Voor de inductanties L1 en L2 volgt:
L1 
n12 20002

 20 H
R1 2  105
L2 
n22
400 2

 0.48 H
R2 33  10 4
3
 In het geval van verzadiging geldt:
dB 
0  


R
dH 
en
L0
c Bereken de magnetisatiestroom en vergelijk deze met de stroom in de
primaire wikkeling.
 De magnetisatiestroom is die stroom die nodig is om de flux te
onderhouden
 Uit de wet van Ampère volgt:
i 
H l
n
i1 
H  l1 B l1  1 l1 
E 2 R
      R 

n1
 n1 A  n1 n1
2f  n1 n1

E 2 1 220 2 1
 

 49.5 mA
2f L1
2 50 20
 Gegeven is de stroom in de secundaire winding, i2, gezocht is een
uitdrukking met i1 afhankelijk van i2
 Uit de wet van behoud van energie, met P=ei
P1  P2

e1  i1  e2  i2

e2 i1

e1 i2
 Uit de uitdrukking van de e.m.k. volgt:
en
d
dt
en
2  0.5  1
d
d 0.5  1 
n2  2 n2 
e2
n
dt 
dt

 0.5  2
d
e1 n  d1
n1
n1  1
1
dt
dt
 Hieruit volgt:
e2 i1
n
  0.5 2
e1 i2
n1

 n 
400 

i1  i2   0.5 2   10   0.5
 1 A
n
2000


1 

 Er geldt dat de primaire stroom groter is dan de magnetisatiestroom
( i1  i1 ), dus de flux kan in stand gehouden worden
4
Opgave DC-motor – oefening 2
a. bereken Emin
b. Als E gelijk is aan 50 Volt, wat is dan de waarde van de rotatiesnelheid
?
c. Waarom is A’ uit ijzer vervaardigd?
l
Gegeven:
A’ en B’: Fe
B=0.1 T
D=20cm
Mlast=5 Nm
N=200
l=20cm
5
Uitwerking DC-motor – oefening 2
a. bereken Emin
 Gegeven is:
o DC-motor met n=200 windingen
o A’ en B’ zijn uit ijzer vervaardigd
o B=0.1 Tesla
o D=20cm en l=20cm
o M1ast=5 Nm (lastkoppel)
 Voor het koppel geldt:
met Fwikkeling  B  l 
i
2
M wikkeling  Fwikkeling 
D
i D
 Bl  
2
2 2
i/2 i
n/2
i/2
e = B .l.v
B

D
i  D n  B l i


M rotor  n  M wikkeling  n   Fwikkeling    n   B  l    
2
2 2
4


 Om de motor op te starten moet het last koppel overwonnen worden
Mrotor  Mtraagheid  Mlast
Mtraagheid  i
d
0
dt
M  Mlast
 Hieruit volgt:
i D

Mlast  n   B  l   

2 2

4 Mlast
45
20
i


 25 A
2
2
n  B  l  D 200  0.1  20  10   20  10  0.8
 De spanning E hangt af van de spanning over de rotor (Erotor) en de
spanning over de weerstand R, er geldt:
E  R  i  Erotor  R  i  B  l  v 
n
  D  n
 R i  B l 

2
 2  2
 In het geval van een stilstaande rotor (=0) geldt:
E  R  i  5  25  125 Volt
6
b. Als E gelijk is aan 50 Volt, wat is dan de waarde van de rotatiesnelheid
?
 Voor E geldt:
E  R  i  Erotor  R  i  B  l  v  
 Voor i geldt:
i
4 Mlast
n Bl  D
als
 Hieruit volgt
n
D n

 R  i   B  l    
2
2 2

d
0
dt
(constante omloopsnelheid)
 4 Mlast 
  D  n
E  R
  Bl 

n Bl  D
 2  2

 4 Mlast 


4
   E  R
 
n Bl  D  n Bl  D




45


  50  5
 50  125  5  375 rad/sec
 
200  0.1  0.2  0.2  200  0.1  0.2  0.2

4
c. Waarom is A’ uit ijzer vervaardigd?
 IJzer is zacht magnetisch met Ramax=250000
 De magnetische krachtlijnen vanuit de lucht gaan vrijwel evenwijdig
met het oppervlak lopen
 Hierdoor wordt geleiding van de magnetisch flux verkregen.
7
Opgave transformator – oefening 3
De onderste figuur is de magnetisatiecurve van de ijzerkern in de
bovenstaande transformator. De doorsnede A van de ijzerkern bedraagt 10
cm2. De lengte l van de ijzerkern is 50 cm.
a Bepaal het aantal windingen n1 zodat net geen verzadiging optreedt in de
ijzerkern. Leg uit waarom zulks vermeden moet worden.
b Stel dat R= en C=0. Bereken dan de amplitudo van de
magnetisatiestroom door de wikkeling n1.
c Schets het tijdsverloop van de spanning tussen A en B in de volgende
veronderstellingen:
1 C = 0, R =50 
2 C = 1000 F, R=
3 C = 1000 F, R=50 
d Waartoe dient zoiets?
8
Uitwerking transformator – oefening 3
a Bepaal het aantal windingen n1 zodat net geen verzadiging optreedt in de
ijzerkern. Leg uit waarom zulks vermeden moet worden.
 Gegeven:
A = 10 cm2
dB
0.5

dH 250
l = 50 cm
Bmax = 0.5 Tesla
Eeff = 220 Volt
n2 = n3 = 0.1n1
f = 50 Hz
 Er geldt voor de maximale flux (geen verzadiging):
max  Bmax  A
 Het verband tussen het aantal windingen n en de flux  volgt uit:
en
d
dt
 t  
E 2
sin( t )
n 
en
e  E 2  cos(t )

 max 
E 2
n  2f
 Voor het aantal wikkelingen n geldt dus:
n
E 2
E 2
220 2


 1980.7
 max  2f Bmax  A  2f 0.5  10  10 4   2  50
Kies: n1 = 2000 wikkelingen
b Stel dat R= en C=0. Bereken dan de amplitudo van de
magnetisatiestroom door de wikkeling n1.
 Voor de magnetisatiestroom geldt:
H  l 250  50  10 2 
i 

 6.25  10 2 A
n1
2000
9
c Schets het tijdsverloop van de spanning tussen A en B in de volgende
veronderstellingen:
1 C = 0, R =50 
 Er geldt:
en
d
dt
en
e 3  e 2  n2
1  2  3  
en
n3  n2  0.1  n1
d
d
 0.1n1
 0.1e1
dt
dt
D1
 Uit de stroomwet van Kirchof volgt:
en
i AB  i1  i2
i1 , i2  0 (diode)
e2
 Uit de spanningswet van Kirchof volgt:
e2  VD1  VAB
e3  VD 2  VAB
+
-
-
R
e3
VAB  R  i AB
+
iab
B
 Uit de wet van Ohm volgt:
i1
+
-
C
i2
 Stel nu dat e2=e3>0 en i2>0 en VD20, dan:
D2
e3   R(i1  i2 )
>0
>0 ?? kan niet, dus i2=0
 Stel nu dat i1=0
e2  R  i1
>0 =0 ??
kan niet, dus i1>0
 Hieruit volgt dat e2=VAB
 Analoog volgt dat e3=-VAB indien e2=e3<0
10
A
 DUS:
e2
e3
t
VAB
t
2 C = 1000 F, R=
 i1, i20
 lading kan niet weg
 de condensator wordt opgeladen
 DUS:
VAB
t
3 C = 1000 F, R=50 
 Nu is er een RC circuit waarvoor geldt:
i
V
dV
 C
R
dt
V  V0  e


dV
1

V 0
dt RC
t
RC
  RC  50  1000  106   50  103 sec
 De periode van de wisselspanning is:
T
1
1

 20  103 sec
f 50
 Hieruit volgt dat de condensator zich niet volledig kan ontladen
11
 DUS:
VAB
t
12
Opgave elektromagneet – oefening 4
Gegeven een elektromagneet zoals hieronder afgebeeld. Het anker A wordt
in rust door veer V tegen stootblokken a en b geduwd met een kracht F=0.1
Newton. De luchtspleet ll = 1 mm. De poolschoenen P1 en P2 zijn met
rubber bekleed met een dikte lr = 0.1 mm. Anker en magneet zijn van
weekijzer met een  = . Het aantal wikkelingen n = 100 en de doorsnede O
van de poolschoenen is 4 cm2.
1. Bereken de stroom I, geleverd door een gelijkstroombron, nodig om het
anker van de stootblokken naar de rubberen bekleding te trekken *.
2. Bereken tot hoever de stroom I moet verlaagd worden opdat het anker
terug tegen de stootblokken wordt geduwd *.
3. Tijdens beide verplaatsingen ontstaat er een spanning aan de klemmen
van de spoel. Leg uit waarom en geef de richting van de eventuele
spanning aan voor beide bewegingen.
4. Wat gebeurt er als we een transformator zouden aansluiten op een
gelijkspanningsbron?
* neem aan dat de veerkracht over die kleine verplaatsingsafstand constant
is.
13
Uitwerking opgave elektromagneet – oefening 4
1. Bereken de stroom I, geleverd door een gelijkstroombron, nodig om het
anker van de stootblokken naar de rubberen bekleding te trekken.
 Volgens de wet van virtuele arbeid geldt:
mechanische energie = magnetische energie + energie geleverd
aan de bron I
 L I2 
   e  I dt
Fdx  d 
 2 
 Voor het bepalen van I zijn de waarden van de inductantie L en de
e.m.k. e nodig
 Voor de inductantie L geldt:
n2
L
R
R
en
l
A
(met   0   r )
R  R fe  R lucht  R Rubber
R
l FE
 0   FE  A

2  llucht
2  l rubber

 0   lucht  A  0   rubber  A
met lucht   rubber  1
en
FE  
DUS:
R
2  llucht  l rubber 
2x

0  A
0  A
L
n 2 0 A
2x
met x  (llucht  lrubber )
 Voor e geldt:
en
d d ( LI )

dt
dt
d ( n ) 

L 

di 

 Invullen in de vergelijking van de virtuele arbeid:
 L I2 
   e  I dt
Fdx  d 
2


14
F
 En
I 2 dL
dt I 2 dL d LI 
dt I 2 dL
dL
I 2 dL
  e  I  

I 

 I2 

2 dx
dx 2 dx
dt
dx 2 dx
dx
2 dx
 n 2 0 A 

d 
2 x 
n 2 0 A
dL



dx
dx
2x2
 Hieruit volgt F als functie van I:
I 2 dL n 2 I 2  0 A
F 

2 dx
4x2
I
4  F  x2

n 2  0  A
4  0.1  1.1  10 3 
 310.3 mA
1002  4  10 7  4  10 4 
2
2. Bereken tot hoever de stroom I moet verlaagd worden opdat het anker
terug tegen de stootblokken wordt geduwd.
 Indien het anker terug tegen de stootblokken wordt geduwd geldt:

llucht  0
x  lrubber
 Voor I geldt dan:
I
4  F  x2

n 2  0  A
4  0.1  0.1  10 3 
 28.2 mA
1002  4  10 7  4  10 4 
2
3. Tijdens beide verplaatsingen ontstaat er een spanning aan de klemmen
van de spoel. Leg uit waarom en geef de richting van de eventuele
spanning aan voor beide bewegingen.
Beweging naar het anker toe
 llucht wordt kleiner
o R
l
, dus de weerstand R wordt kleiner
A
o L
n2
d
n
, dus met een afnemende R wordt de inductantie L
R
dt
groter
o Hierdoor neemt de flux  toe
15
 Voor de magnetische potentiaal geldt:
  R   , deze is constant vanwege de constante stroombron
(  n I )
 De emk e werkt de fluxverandering tegen ( e  n
d
). Het systeem
dt
probeert de stroom te verminderen door een spanning op te wekken
die de tegengestelde stroom levert.
 DUS:

i
-
e
+
Beweging van het anker af:
 Analoog, de flux neemt af. De emk e probeert de stroom te verhogen
door een spanning op te wekken die extra stroom toevoegt.
 DUS:

e
-
i
16
+
4 Wat gebeurt er als we een transformator zouden aansluiten op een
gelijkspanningsbron?
 Er geldt:
en
d
dt
 Gelijkspanning resulteert in een toename van de flux  en dus een
toename van de stroom i
 Hierdoor wordt de bron opgeblazen ofwel branden de wikkelingen
door.
17
Opgave gelijkstroommotor – oefening 5
Beschouw een gelijkstroommotor. De weerstand van een ankerwikkeling is
Ra. Het aantal ankerwikkelingen is Na. De weerstand van een veldwikkeling
is Rv. Het aantal veldwikkelingen is Nv. De reluctantie van de magnetische
keten waarop de veldwikkelingen liggen is R1. U mag aannemen dat deze
magnetische keten een constante permeabiliteit en doorsnede heeft over zijn
ganse lengte (wat in werkelijkheid natuurlijk niet het geval kan zijn). Zowel
de ankerspanning als de veldspanning wordt verkregen uit een ideale
gelijkspanningsbron E.
a. Teken het schema van dit systeem (vierpoolmodel).
b. Bereken de koppel-toerental karakteristiek in functie van de gegeven
grootheden.
c. Bereken de impedantie die de gelijkspanningsbron ziet.
d. Wat verandert er indien de gelijkspanningsbron niet ideaal is? Hoe zou u
dan de koppel-toerental karakteristiek berekenen?
18
Uitwerking opgave gelijkstroommotor – oefening 5
a Teken het schema van dit systeem (vierpoolmodel).
anker
Ra=0.25*(Nara )
stator
Rv=Nvrv
e
Na
E
 M
+
-
L
 Voor het anker geldt:
e  i  M 
n
n 
D

e   B  l  v     B  l        B  A  B  D  l 
2
2 
2
2
n
n
e
   k    k 
2
2
Hier geldt:
E  Ra  I a  k    
met
k
Na
2
Verder geldt:
M  n Bl 
D i
n
 
  i  k   i
2 2 2
 Voor de stator geldt:
dI
E  Rv  I v  L v
dt
en
N v2
L
Rl
en
  L  Iv
19
b Bereken de koppel-toerental karakteristiek in functie van de gegeven
grootheden.
 Afleiden  als functie van Iv:
di
d
eN
en
dt
dt
L

Iv
Nv
dI
 Indien v  0 , geldt:
dt
E
Iv 
Rv
eL

LN
d
di

d
L

di N
 Dus:

L E
N v Rv
 Invullen in E  Ra  I a  k     en M  k    I a geeft:
E  Ra  I a  k 
L E

N v Rv
en
M k
L E
 Ia
N v Rv
 Uitwerken twee vergelijkingen tot een uitdrukking met M als functie
van :

kL 
Ra  I a  E 1 

 N v Rv 
invullen in M:
 L E2   k  l   1
  1 
en
M  k  

N v Rv  Ra
 N v Rv  
N r
N
N2
Ra  a a , Rv  N v rv , k  a , L  v
4
2
Rl
dus
 N v2  2

E
k

Rl 
k  L  E2 1 
k  L  
1

M 


1 

2
N v  N v rv Ra  N v  N v rv 
N v  rv
 N a ra

 4

 N v2  
  
 k  
Rl  


1 

N v2  rv 



 
20
 Na  2
4
E
4k E
1 
k  
1
2 

M 


1 

rv  Rl
N a ra  rv  Rl 
rv  Rl
N a ra
2
2  E2
M 
  rv  Rl  ra
  Na  
  2    


1 

rv  Rl 



  Na   

1  

2


 rv  Rl 

c Bereken de impedantie die de gelijkspanningsbron ziet.
 Uit opgave b volgt het verband tussen Ia en E, waaruit de
vervangingsweerstand van het anker volgt, nl.:

kL   1
I a  E 1 

N v Rv   Ra


 

 Vanuit de positie van de gelijkspanningsbron staan de statorweerstand en de anker-weerstand parallel, dus:
Rv 
Ra

k  L  
1 

N
R
Ra
v v 

Rtotaal  Rv //

R


k  L 
a
1 
 Rv 

k

L  
N v Rv 

1 

N v Rv 

Rtotaal 
Rtotaal 
Rv  Ra




Ra
k  L  



 Rv 
1 
N
R


k

L


v
v



1 
 

N v Rv  

Rv  Ra




Ra
Ra
k  L  
k  L  
Rv 
 Rv 


N v Rv
N v Rv 



k  L  
k

L


 1 

1 





N
R
N
R
v v 
v v 



21
Rtotaal 
Rv  Ra
Rv  Ra

R  k  L 
k  L 
( Rv  Ra ) 
( Rv  Ra )  v
Nv
N v Rv
d Wat verandert er indien de gelijkspanningsbron niet ideaal is? Hoe zou u
dan de koppel-toerental karakteristiek berekenen?
 Een niet ideale bron heeft een interne weerstand Rintern
 Voor de spanning over het gehele circuit geldt nu (zie schema):
V  R i
en
V  E  Ri  i
 V 

V  E  Ri 
 Rtotaal 

Ri 
E
V 1 
Rtotaal 

V  E
Rintern
E
VR
totaal
Rtotaal
Ri  Rtotaal
 In de koppel-toerental karakteristiek kan nu E vervangen worden door
V.
22