(Rust-) Massa

(Rust-) Massa
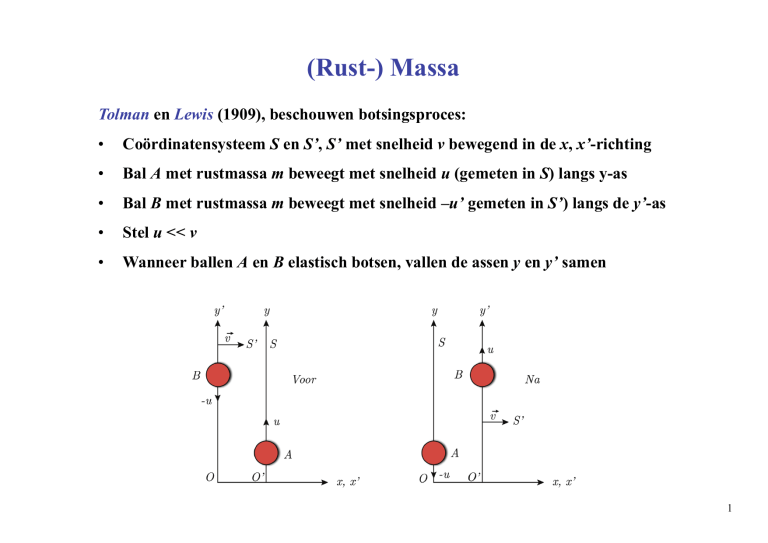
Tolman en Lewis (1909), beschouwen botsingsproces:
•
Coördinatensysteem S en S’, S’ met snelheid v bewegend in de x, x’-richting
•
Bal A met rustmassa m beweegt met snelheid u (gemeten in S) langs y-as
•
Bal B met rustmassa m beweegt met snelheid –u’ gemeten in S’) langs de y’-as
•
Stel u << v
•
Wanneer ballen A en B elastisch botsen, vallen de assen y en y’ samen
1
•
Waarnemer in S ziet bal A met snelheid +u botsen en vervolgens met snelheid -u terugkomen:
D = -2u
•
Waarnemer in S’ ziet bal B met snelheid -u botsen en vervolgens met snelheid +u terugkomen:
D = +2u
Snelheid van bal B gemeten in systeem S is
De afbeelding k an momenteel niet worden weergegev en.
voor de botsing: -u 1 en daarna:
+u 1 -
v2
c2
v2
c2
Stel:
•
De botsing wordt gemeten in S
•
De massa van bal A wordt gedefinieerd als m0
(d.w.z. voor u << v, m0  rustmassa)
•
De massa van bal B, gemeten in S, wordt gedefinieerd als m
2
Als nu A en B een ‘gesloten’ systeem vormen voor en
na de elastische botsing, dan geldt impulsbehoud:
Voor botsing:
Na botsing:

 m0 u
 m0 u
2m0 u
Impuls bal A :
Impuls bal B :
 mu 1 
v2
c
 mu 1 
2
v2
c
 2mu 1 
2
v2
c2
Uit de impulsbalans volgt dan:
-2m0u + 2mu 1 -
v2
c
2
= 0  m0 = m 1 -
v2
c2
Met andere woorden:
m =
m0
1-
v
2
c
2
,
px º mvx =
m0vx
1-
v2
c2
3
Massa in beweging...
5
4
m
m0
3
m
=
m0
2
1
1-
v2
c2
1
0
0
0,2
0,4
0,6 v / c 0,8
1
De (geschaalde) massa als functie van de (geschaalde) snelheid
4
Impuls- en energiebehoud
2e hoofdwet van Newton:
De impulsverandering van een lichaam is evenredig met de
resulterende kracht die op het lichaam wordt uitgeoefend:


d
dp

F µ ( mv ) =
dt
dt
en levert met de juiste keuze van eenheden:


d
dv

 dm
F = ( mv ) = m
+v
dt
dt
dt
Hiermee kan de verandering van kinetische energie geschreven worden als:
dEkin º Fdx = m
dv
dm
dx + v
dx = mvdv + v 2dm
dt
dt
5
dEkin º Fdx = m
met: m =
m0
1-
v2
c
dv
dm
dx + v
dx = mvdv + v 2dm
dt
dt
en dm =
m0
c2
2
vdv
3
v 2 ö2
=
æ
çç 1 - ÷÷
÷
ççè
c 2 ÷ø
(
mvdv
(c 2 - v 2 )
)
geeft dit: dEkin = mvdv + v 2dm = c 2 - v 2 dm + v 2dm
= c 2dm =
m0vdv
3
v 2 ö2
æ
çç 1 - ÷÷
÷
ççè
c 2 ÷ø
6
v
Ekin
Ekin =
ò
0
v
dEkin =
ò
0
m0vdv
3
v 2 ö2
æ
çç 1 - ÷÷
÷
ççè
c 2 ø÷
=
m0c 2
1-
=
v2
c
2
m0c 2
1-
0
v2
- m0c 2 = mc 2 - m0c 2
c2
De totale energie is gelijk aan de som van rustmassa en kinetische energie:
Etot º mc 2 = Ekin + m0c 2
 2
p
c
2
= gm0c = 
v
 Etot =
m0c 2
 2
pc
( )
1- 2
Etot
æ
çç
çç
çç met p º mv =
çç
çèç
ö÷
 ÷÷
m0v ÷÷
÷
 2 ÷÷
v ÷
1 - 2 ÷÷÷
c ø

 Etot 2 - p 2c 2 = m02c 4
7
2
1,5

p
é MeV / c ù
ë
û
Ekin
1
é MeV ù
ë
û
Impuls
0,5
Kinetische energie
0
0
0,2
0,4
0,6
0,8
1
b = vb c
Impuls en kinetische energie voor een versneld elektron als
functie van zijn (geschaalde) snelheid
8
Relativistische kinematica:

Ondanks dat energie en impuls ( E , p ) verschillend zijn wanneer zij gemeten
worden in de inertiaalstelsels S en S’, vinden we dat:

E 2 - p 2c 2 = m02c 4
invariant is onder Lorentztransformaties. Dit geldt eveneens voor de relatie:
c 2t 2 - x 2 - y 2 - z 2 = c 2t '2 - x '2 - y '2 - z '2
We definiëren de ruimte-tijd vector als een ‘4-vector’:
x 0 º ct,
æ x 0 ö÷
çç ÷
çç 1 ÷÷
çç x ÷÷÷
m
x º ç 2÷,
çç x ÷÷
çç ÷÷
çç x 3 ÷÷÷
è ø
x 1 º x,
x 2 º y,
x3 º z
met:
( m = 0, 1, 2, 3 )
xm º (x0
x1 x 2
x 3 ),
( m = 0, 1, 2, 3 )
9
De Lorentzinvariante grootheid:
2
2
2
I = ct - x - y - z
2
= (x
2
2
2
2
) - (x ) - (x ) - (x )
2
2
2
2
0
1
2
3
= (x ' ) - (x ' ) - (x ' ) - (x ' )
0
1
2
3
kan geschreven worden als het scalaire product van de twee 4-vectoren…
x mx m = x mx m º x 0x 0 - x1x 1 - x 2x 2 - x 3x 3
Of algemeen:
a mbm = a mb m = a 0b 0 - a 1b1 - a 2b 2 - a 3b 3
10
…maar dan kunnen we met de 4-vector…
æE
ö÷ æ E  ÷ö
ç
p = ç , px , py , pz ÷÷ = çç , p ÷÷
çè c
ø çè c ø
m
Einstein’s uitdrukking voor de Lorentzinvariante massa
E 2 - p 2c 2 = m02c 4
eenvoudig schrijven als:
m
pm p =
E2
c2

- p 2 = m02c 2
11
Veel-deeltjes systemen:
De ‘rustmassa’ van een veel-deeltjes systeem kan
eenvoudig geïntroduceerd worden...
Beschouw:
•
Twee botsende deeltjes a en b
•
Impuls-energie van deeltjes a en b: pa en pb
•
Rustmassa van deeltjes a en b: ma en mb
pa2 = ma2c 2
pb2 = mb2c 2
Definieer ‘invariante massa’
(in het kwadraat):
( pa
2
2 2
+ pb ) = mab
c
12
Heavyside-Lorentz eenheden…
Dimensies van 3 belangrijkste grootheden in subatomaire fysica: { M , L,T }
[c ] = [snelheid ] = LT -1
[ ] = [lengte ´ impuls ] = ML2T -1
2
[E ] = [massa ´ ( snelheid ) ] = ML2T -2
L = [ ][c ][E ]-1
M = [E ][c ]-2
T = [ ][E ]-1
Met  = c = 1 :
L = [E ]-1
M = [E ]
T = [E ]-1
13
Twee-deeltjes botsing; twee deeltjes eindtoestand
Beschouw:
•
Twee-deeltjes reactie a + b
•
Impuls-energie etc. : pa, pb, ma, mb etc.
•
De botsing verloopt elastisch d.w.z. c = a; d = b of c = b; d = a
•
De botsing verloopt inelastisch: c  a en c  b
Het kwadraat van de invariante
massa van a en b (c = 1 !):
( pa
2
2
+ pb ) = mab
wordt de energie (in het kwadraat) in
het zwaartepunt genoemd
14
Behoud van energie en impuls impliceert dat:
( pa
2
2
2
2
+ pb ) = ( pc + pd ) = mab
= mcd
Ea + Eb = Ec + Ed




pa + pb = pc + pd
Het kwadraat van de zwaartepuntenergie wordt aangeduid met:
2
2
s º ( pa + pb ) = ( pc + pd )
M.b.v. pa + pb = pc + pd kunnen twee andere ‘behouden’
(Lorentzinvariante) relaties gedefinieerd worden:
2
2
2
2
t º ( pa - pc ) = ( pb - pd )
u º ( pa - pd ) = ( pb - pc )
s, t en u zijn de Lorentzinvariante Mandelstam variabelen.
Ga na dat geldt: s + t + u = ma2 + mb2 + mc2 + md2
15
Uit energie- en impulsbehoud volgt (ga na!):
Ec =
s + mc2 - md2
2 s


pc = pd =
=
(
Ec2 - mc2
2
s - ( mc + md )
)(
2
s - ( mc - md )
)
2 s
Om de reactie a + b  c + d kinematisch mogelijk te maken moet gelden dat:
2
2
s = ( pa + pb ) = ( pc + pd )
2
 
= mc2 + md2 + 2 ( Ec Ed - pc ⋅ pd ) ³ ( mc + md )
De zwaartepuntenergie
s is een van de cruciale parameters van deeltjesversnellers
en bepaalt ‘hoe diep we in de materie kunnen indringen’
16
‘Fixed target’ vs ‘Collider’
Beschouw de volgende typen deeltjesversnellers:
•
Een enkele deeltjes bundel waarmee op een doel
wordt geschoten
•
Twee deeltjes bundels van identieke deeltjes met
gelijke, maar tegengestelde impuls
•
‘Fixed target’
De massa (M) van het
doel is cruciaal (!):
2
s = ( p + P ) = m 2 + M 2 + 2EM
17
Twee bundels deeltjes :
•
‘Collider’
De massa’s van de deeltjes zijn voor E >> m irrelevant !

s = ( p1 + p2 ) = 2m 2 + 2 ( E 2 + p 2 )
2
= 2m 2 + 2E 2 + 2 ( E 2 - m 2 ) = 4E 2
Met een ‘collider’ worden dus i.h.a. hogere
zwaartepuntenergieën bereikt !
18
Deeltjes versnellers
De eigenschappen van deeltjesbundels (en het ‘target’) zijn zowel een
belangrijke factor voor het ontwerp van de experimenten als bepalend voor de
fysica die in de botsingen bestudeerd kan worden:
•
•
•
•
de bundelenergie bepaalt in sterke mate het ‘massa-interval’ van de deeltjes
(zwaartepuntenergie) die in de interactie geproduceerd kunnen worden en kan de
werkzame doorsnede voor bepaalde processen sterk beïnvloeden
de deeltjesflux bepaalt naast de werkzame doorsnede voor een geselecteerd proces,
hoe vaak dit proces uiteindelijk per tijdseenheid op zal treden
de ‘duty-cycle’ van een versneller geeft de fractie van de tijd dat de versneller
deeltjes aan het experiment levert
de structuur van de bundel in de tijd is belangrijk om te bepalen wanneer het
experiment operationeel moet zijn. Het definieert de tijd tussen twee potentieel
interessante botsingen. Een te snelle opeenvolging van botsingen kan leiden tot
‘dode tijd’; een periode waarin het experiment nog bezig is om gegevens van een
voorgaande botsing te verwerken, terwijl een nieuwe botsing zich al aandient en
dus verloren kan gaan.
19
Versnellen met continu potentiaalverschil
Voorbeeld: de elektronenmicroscoop. Omstreeks 1920 werd de eerste
hoogspanning ‘deeltjesversneller’ in Cambridge op basis van de kathodestraalbuis
door Cockcroft en Walton ontwikkeld. Zij plaatsten twee elektroden in een
vacuümvat en bereikten een potentiaalverschil van  105 V. Begin jaren dertig
ontwikkelden Cockcroft en Walton een experimentele opstelling om protonen te
versnellen en vervolgens te laten penetreren in lithiumkernen .
20
Zij slaagden er in om een elektrisch systeem te construeren dat  800 kVolt kon
leveren. Dit potentiaalverschil werd verkregen met behulp van een wisselspanning
en een combinatie van gelijkrichters plus een cascadeschakeling van capaciteiten
(om herhaalde spanningsverdubbeling te realiseren:
Cockcroft-Walton
moderne uitvoering
21
Daar er vrijwel geen stroom aan deze schakeling ontrokken wordt, blijft de
opgebouwde spanning gehandhaafd…
Cockcroft en Walton realiseerden in 1932 de eerste nucleaire transformatie:
1
1
H  37 Li  24 He  24 He
Detectie van de  -deeltjes leverde het eerste experimentele bewijs voor Einstein’s relatie
E  mc 2 ! Beiden ontvingen in 1951 de Nobelprijs voor de fysica.
In 1932, vrijwel gelijktijdig met het
experiment van Cockcroft en Walton,
construeerde Van de Graaff in de Verenigde
Staten een eerste versneller, waarvoor het
potentiaalverschil werd opgebouwd door
middel van ladingstransport naar een
geïsoleerde elektrode.
22
Een isolatieband verbindt twee roterende
assen waarvan er een zich op het
aardpotentiaal bevindt en de ander binnen
de geïsoleerde elektrode. Door middel van
wrijving wordt de isolatieband met
geïnduceerde lading ‘opgeladen’.
Deze lading wordt vervolgens getransporteerd
naar de elektrode die via corona ontlading een
tweede elektrode oplaadt.
Met deze techniek zijn spanningsverschillen tot
20  30 MVolt bereikt. De generatoren zijn
veelvuldig bij diverse versnellers toegepast.
23
Van de Graaff generatoren bij Notre Dame University (V.S.) en CERN voor het
opwekken van potentiaalverschillen van meer dan 1 MVolt .
24
Variabel potentiaalverschil
Het versnellen van geladen deeltjes in een hoogfrequent elektrisch veld werd in
1928 door de Noor Wideröe voor het eerst voorgesteld. In dat jaar bouwde hij
aan de Technische Hochschule van Aken een eerste, op dit principe gebaseerde,
versneller waarin hij tevens driftbuizen toepaste:
De impulsverandering dat een geladen deeltje in een

elektrisch (magnetisch) veld ondervindt is
  
dp 
proportioneel met de Lorentz kracht op dit deeltje:
 F  q EvB
dt


25
Het klassieke cyclotron
Door Wideröe geïnspireerd, bouwden
Lawrence en Livingston in 1931 bij
Berkeley Radiation Laboratory in de
Verenigde Staten, een apparaat waarmee
met behulp van een wisselend magnetisch
veld deeltjes versneld konden worden
(rechts).
De eerste stap werd door
Lawrence gezet met het
ontwerp en de constructie
van een 12.5 cm diameter
prototype (links).
26
Een cyclotron bestaat uit een vacuümkamer, ingesloten tussen de polen van een
cirkelvormige dipool magneet:
Binnen in de vacuümkamer worden twee halfcirkelvormige ‘dozen’ op korte afstand van
elkaar geplaatst (links) en verbonden met een wisselspanning bron. De ionen worden in
het centrum geïnjecteerd en volgen een cirkelbaan in het magnetische veld (rechts).
27
Het synchrocyclotron
Voor de versnelling van deeltjes naar veel hogere energie ( v  c ) is de omlooptijd niet
meer onafhankelijk van de snelheid. De kromtestraal neemt evenredig toe met de
impuls, maar de omlooptijd wordt langer en de omloopfrequentie dus lager!
CERN’s 600 MeV
synchrocyclotron
gebouwd in 1957.
28
Door de frequentie van de hoogspanningsbron te moduleren, blijven de versnelde
deeltjes synchroon met de versnellingsbron bij contant magneetveld. Modulatie wordt
verkregen door variatie van een capaciteit of een zelfinductie in het hoogfrequente
elektronische circuit.
De consequentie van deze techniek is wel dat na
injectie alle deeltjes versneld worden tot een
maximale energie bepaald door  , B etc. Injectie
van nieuwe deeltjes heeft alleen dan zin wanneer de
versnelde deeltjes geëxtraheerd zijn! Het
synchrocyclotron produceert dus niet doorlopend
versnelde deeltjes, maar groepen van deeltjes met
de herhalingfrequentie van de modulatiecyclus.
29
Synchrotrons en botsingmachines
Om hogere energieën te bereiken wordt een ring van magneten opgesteld. Vervolgens worden
zowel het magnetische veld als de versnellingsfrequentie synchroon gemoduleerd. Hierbij
treedt een zwakke focussering op. Sterke focussering werd begin jaren ‘50 ontwikkeld door
de Griek Christofilos en door Courant, Livingston en Snyder.
Tegenwoordig worden focuserende en defocuserende quadrupool magneten gebruikt.
30
Het principe van sterke focussering is toegepast in het CERN-protonsynchrotron (PS,
Omtrek 800 m , energie 28 GeV ) dat in 1959 in bedrijf werd genomen en het Alternating Gradient
Synchrotron (AGS, omtrek 800 m , energie 33GeV ) van Brookhaven (BNL), dat in 1960 gereed
kwam. Economische overwegingen beperken de energie van synchrotrons met ‘conventionele’,
warme magneten, tot  450 GeV in het geval van protonen ( Bmax  1.8 Tesla voordat
verzadiging in de ijzeren magneetpolen optreedt).
Voorbeelden zijn het protonsynchrotron bij het Fermi National Accelerator Laboratory
(FNAL, Chicago, omtrek 6.4 km , maximale protonenergie  450 GeV ),
in bedrijf sinds 1972, en het Super Proton Synchrotron (SPS, omtrek 6.4 km ,
maximale protonenergie eveneens  450 GeV ), in bedrijf bij het CERN sinds 1976.
Hoofdstukken uit de Hoge Energie Fysica
31
Wanneer geladen deeltjes een cirkelbaan met straal  doorlopen, treedt energieverlies op ten
gevolge van de centripetale versnelling die zij ondervinden in het magnetische veld; er worden
fotonen geëmitteerd (vergelijk met de elektronen die in een radioantenne heen en weer
bewegen en zo elektromagnetische straling uitzenden). Bij niet-relativistische snelheden wordt
gesproken van cyclotron straling terwijl synchrotron straling het relativistische regime
kenmerkt. De hoeveelheid afgestraald vermogen kan berekend worden met behulp van de
(niet relativistische) formule van Larmor voor elektrische dipool straling:
2q 2 a 2
P 
3c3
Hierin is q de elektrische lading en a de centripetale versnelling van het geladen deeltje, en c
de lichtsnelheid. De relativistische uitdrukking volgt door het afgestraalde vermogen te
beschouwen in het rustsysteem van het deeltje en vervolgens een Lorentz transformatie toe
te passen. De versnelling volgt dan eenvoudig uit de centripetale versnelling v 2  ( mq is de
rustmassa van het versnelde deeltje; Lorentztranformatie: t’, v’ t, v):
a
Fcentripetaal
mq
2
1 dp
1 d  mq v ' 1 d   mq v 
2 dv
2 v







mq dt ' mq
dt '
mq
dt
dt
32
Substitutie geeft:
2q 2 4 v 4
P 
3c 3  2
Per omloop raakt een enkel elektron met een energie van 100 GeV in een synchrotron met een
straal   4300 m (de voormalige LEP ring bij CERN in Genève) het volgende vermogen kwijt:
2e 2 4 c
P 
3 2
2  8.987  109 Nm 2 C 2 1.6  1019 C  196000   3  108 m s 
2

3   4300m 
4
2
 3.7  106 Watt
Aangezien  bijzonder groot is (   196000 ) en   1, kunnen we v in de teller vervangen
door c . Dit vermogensverlies lijkt in eerste instantie klein maar treedt op voor ieder
elektron! Het energieverlies ten gevolge van synchrotron straling per omloop is dan:
33
2
4 q 2 v 3 4 4 q 2 3 4
E 
 P 

 
3
v
3c 3 
In de relativistische limiet met   1 en E  mc 2   mq c 2 levert dit de volgende
uitdrukking:
4 q 2 E 4
E 
3 mq4 c 4
Het energieverlies is proportioneel met  mq4 en dus voor elektronen veel groter dan
voor protonen (bij dezelfde energie en straal van de baan):
Eelektron
E proton
4
 mp 
13

  10
 me 
Om stabiele bundels te kunnen garanderen, moet dit energieverlies gecompenseerd
worden met behulp van hoogfrequente elektromagnetische velden. In een circulaire
machine is een hoogenergetische protonenbundel dus eenvoudiger te realiseren dan
een hoogenergetische elektronenbundel!
34
Beknopt overzicht deeltjesversnellers in het lab…
35
…en kosmische versnellers!
36