Huiswerk VI Continue Wiskunde

Huiswerk VI
Continue Wiskunde
inleveren voor of op 22 oktober
Laat de afbeelding f : R2 → R2 gedefinieerd zijn door
f (x, y) = (sin(x) cosh(y), cos(x) sinh(y)),
waar
cosh(y) =
(1)
1 y
(e + e−y )
2
(de cosinus hyperbolicus) en
sinh(y) =
1 y
(e − e−y )
2
(de sinus hyperbolicus). (Terzijde voor diegenen die complexe getallen kennen: de coordinaten van f (x, y) zijn reële en imaginaire delen van sin(z) voor
complexe getallen z = x + iy.)
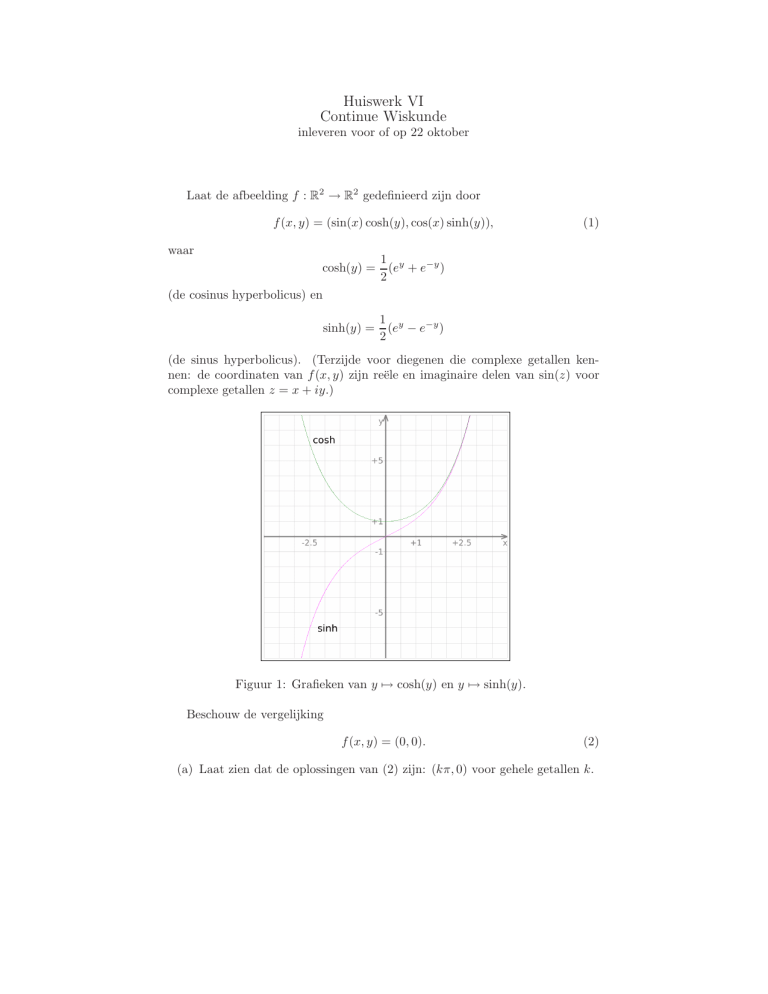
Figuur 1: Grafieken van y 7→ cosh(y) en y 7→ sinh(y).
Beschouw de vergelijking
f (x, y) = (0, 0).
(2)
(a) Laat zien dat de oplossingen van (2) zijn: (kπ, 0) voor gehele getallen k.
Newton’s methode wordt gegeven door een iteratie
(xn+1 , yn+1 ) = N (xn , yn ) = (xn , yn ) − [Df (xn , yn )]
−1
f (xn , yn ).
(3)
(b) Geef een expliciete uitdrukking voor N .
Voor elk van de oplossingen van (2) is er een verzameling van beginwaarden
(x0 , y0 ) ∈ R2 waarvoor de iteratie (xn+1 , yn+1 ) = N (xn , yn ) naar die oplossing
convergeert als n → ∞.
Op de randen van die verzamelingen zijn punten waarvoor de Newton interatie niet convergeert.
(c) (Computer opgave:) Bereken numeriek een figuur die de punten waar Newton iteratie niet naar een oplossing convergeert zichtbaar maakt (eventueel
ook verschillende kleuren voor punten waar Newton iteratie wel naar een
oplossing convergeert, met kleuren afhankelijk van de oplossing waar de
iteratie naartoe convergeert). Een geschikt gebied om mee te rekenen is
[−3π, 3π] bij [−3π, 3π], en eventueel uitgezochte vergrotingen.