hoofdstuk 10 - natuurkunde

10 Zonnestelsel
Cirkelbaan en gravitatiekracht | vwo
Diagnostische toets
1
a
b
c
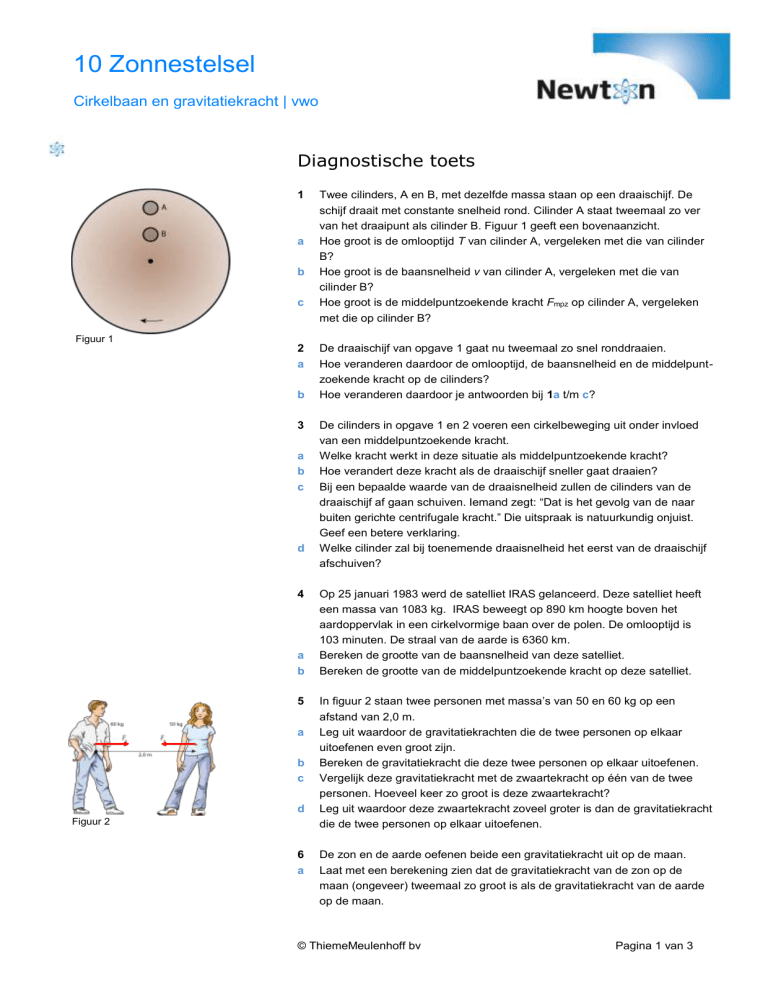
Twee cilinders, A en B, met dezelfde massa staan op een draaischijf. De
schijf draait met constante snelheid rond. Cilinder A staat tweemaal zo ver
van het draaipunt als cilinder B. Figuur 1 geeft een bovenaanzicht.
Hoe groot is de omlooptijd T van cilinder A, vergeleken met die van cilinder
B?
Hoe groot is de baansnelheid v van cilinder A, vergeleken met die van
cilinder B?
Hoe groot is de middelpuntzoekende kracht Fmpz op cilinder A, vergeleken
met die op cilinder B?
Figuur 1
2
a
b
3
a
b
c
d
4
a
b
5
a
b
c
d
Figuur 2
6
a
De draaischijf van opgave 1 gaat nu tweemaal zo snel ronddraaien.
Hoe veranderen daardoor de omlooptijd, de baansnelheid en de middelpuntzoekende kracht op de cilinders?
Hoe veranderen daardoor je antwoorden bij 1a t/m c?
De cilinders in opgave 1 en 2 voeren een cirkelbeweging uit onder invloed
van een middelpuntzoekende kracht.
Welke kracht werkt in deze situatie als middelpuntzoekende kracht?
Hoe verandert deze kracht als de draaischijf sneller gaat draaien?
Bij een bepaalde waarde van de draaisnelheid zullen de cilinders van de
draaischijf af gaan schuiven. Iemand zegt: “Dat is het gevolg van de naar
buiten gerichte centrifugale kracht.” Die uitspraak is natuurkundig onjuist.
Geef een betere verklaring.
Welke cilinder zal bij toenemende draaisnelheid het eerst van de draaischijf
afschuiven?
Op 25 januari 1983 werd de satelliet IRAS gelanceerd. Deze satelliet heeft
een massa van 1083 kg. IRAS beweegt op 890 km hoogte boven het
aardoppervlak in een cirkelvormige baan over de polen. De omlooptijd is
103 minuten. De straal van de aarde is 6360 km.
Bereken de grootte van de baansnelheid van deze satelliet.
Bereken de grootte van de middelpuntzoekende kracht op deze satelliet.
In figuur 2 staan twee personen met massa’s van 50 en 60 kg op een
afstand van 2,0 m.
Leg uit waardoor de gravitatiekrachten die de twee personen op elkaar
uitoefenen even groot zijn.
Bereken de gravitatiekracht die deze twee personen op elkaar uitoefenen.
Vergelijk deze gravitatiekracht met de zwaartekracht op één van de twee
personen. Hoeveel keer zo groot is deze zwaartekracht?
Leg uit waardoor deze zwaartekracht zoveel groter is dan de gravitatiekracht
die de twee personen op elkaar uitoefenen.
De zon en de aarde oefenen beide een gravitatiekracht uit op de maan.
Laat met een berekening zien dat de gravitatiekracht van de zon op de
maan (ongeveer) tweemaal zo groot is als de gravitatiekracht van de aarde
op de maan.
© ThiemeMeulenhoff bv
Pagina 1 van 3
b
Leg uit waardoor de maan dan niet door de zon van de aarde wordt
weggetrokken.
7
De massa van de planeet Jupiter is 300 maal zo groot als die van de aarde.
Je zou dus kunnen denken dat de zwaartekracht op een voorwerp aan het
oppervlak van Jupiter 300 maal zo groot is als de zwaartekracht op dat
voorwerp aan het aardoppervlak. De zwaartekracht op Jupiter blijkt echter
maar net driemaal zo groot te zijn.
Geef hiervoor een verklaring.
Beredeneer met de gegevens uit deze opgave dat de straal van Jupiter
tienmaal zo groot is als die van de aarde.
a
b
8
a
b
9
a
b
c
In de formule voor de gravitatiekracht staan twee massa’s. Voor de
gravitatiekracht tussen de zon en de aarde zijn dat de massa’s van de zon
en de aarde. Toch hangt de omlooptijd van de aarde rond de zon niet af van
de massa van de aarde, wel van de massa van de zon.
Leg uit waardoor de omlooptijd gelijk zou blijven als de massa van de aarde
bijvoorbeeld 100 maal zo groot zou zijn.
Rond een andere ster draait een planeet op dezelfde afstand als de aarde
rond de zon. De massa van de ster is echter 100 maal zo groot als de
massa van de zon.
Leg uit of deze planeet ook in een jaar rond de ster draait, of veel korter of
langer. En als dat veel korter of langer is: hoeveel keer zo kort of lang?
Het International Space Station (ISS) draait op een hoogte van 342 km met
een snelheid van 7,7 km/s rond de aarde.
Welke kracht zorgt ervoor dat het ISS in een cirkelbaan beweegt?
Bereken de gravitatiekracht op een massa van 1 kg op deze hoogte.
Ga met een berekening na dat deze gravitatiekracht precies groot genoeg is
om het ISS in een cirkelbaan te laten bewegen.
10 De massa van de aarde en de afstand aarde-maan zijn bekend (zie Binas).
a Bereken met deze gegevens de baansnelheid van de maan in haar baan
rond de aarde.
b Bereken met behulp van deze baansnelheid de omlooptijd van de maan
rond de aarde. Controleer je antwoord met Binas.
11 Leg uit waardoor de baansnelheid van de planeten in ons zonnestelsel
kleiner is naarmate de afstand van de planeet tot de zon groter is.
12 Leg uit waardoor de omlooptijd van de planeten in ons zonnestelsel groter is
naarmate de afstand van de planeet tot de zon groter is.
13 Het International Space Station (ISS) heeft een massa van 262·103 kg en
draait op een hoogte van 342 km rond de aarde.
a Bereken de gravitatie-energie van het ISS in zijn baan rond de aarde.
b Bereken de arbeid die nodig is om het ISS ‘op te tillen’ vanaf het
aardoppervlak naar zijn baan rond de aarde.
© ThiemeMeulenhoff bv
Pagina 2 van 3
14 Bij een reis naar een andere ster dan de zon moet een ruimtesonde zonder
eigen aandrijving ‘ontsnappen’ aan de gravitatiekracht van het zonnestelsel.
a Leg uit waardoor de ontsnappingssnelheid van de ruimtesonde niet afhangt
van de massa van deze sonde.
b Maak een berekende schatting van de ontsnappingssnelheid van de
ruimtesonde.
15 De gravitatie-energie van een voorwerp op het aardoppervlak en op een
hoogte h boven het aardoppervlak is negatief.
a Leg uit waardoor de gravitatie-energie van het voorwerp altijd negatief is.
b Leg uit dat de gravitatie-energie van het voorwerp toch toeneemt bij
toenemende hoogte h boven het aardoppervlak.
© ThiemeMeulenhoff bv
Pagina 3 van 3