Algebra (verbanden)

h
l
Naam
verband
Lineair
Naam
verband
verband
Lineair
Algebra(verbanden)
verband
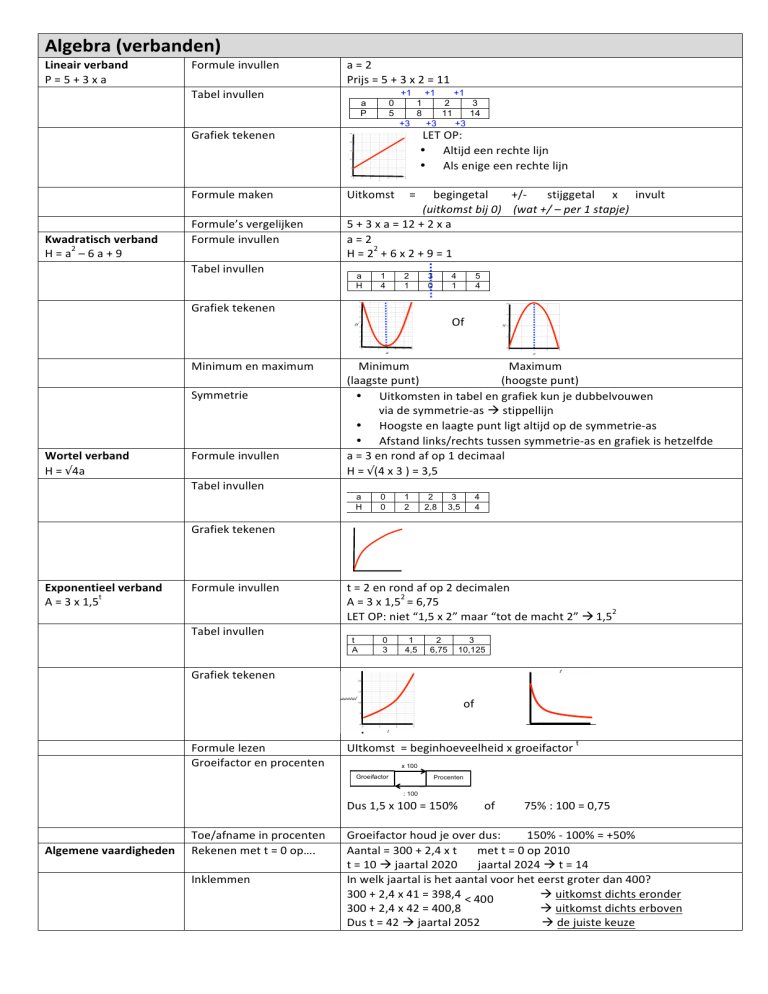
Lineairverband
P=5+3xa
Formule
Tabel
Prijs
= 5 + 3 x aantal
Formule
P = 5 + 3a
Invullen geeft:
Tabel
Altijd rechte lijn
Grafiek
P = 5 + geeft:
3x0=5
Invullen
Altijd rechte lijn
Prijs = 5 + 3 x aantal
P = 5 + 3a
begingetal
Formuleinvullen
stapgrootte
uitkomst
+ of - per
bij
a=0
1stapgrootte
stapje
begingetal
uitkomst
Tabelinvullen
P=5+3x1=8
PP==55++33xx02==5 11
a=2
PP==55++33xx13==8 14
Prijs=5+3x2=11
P!! = 5 + 3 x 2 = 11
Grafiek
Kenmerken
Extra
REGELMAAT: ExtraSom (+) o
Kenmerken
per 1 stapje,
Formule 1
komt er telkensSom (+)
Formule
2
REGELMAAT:
of versc
hetzelfde
Somformu
per
1 stapje,bij of afFormule
1
P
komt er telkens
Formule 2
P
Formule’s
hetzelfde bij of af
Somformule
S
5 + 3a = 2
+114 +1
+1
(1) versch
P!!!!!!!!!!!!
=5+3x3=
Formule’s
verge
!!Tabel
5Extra
+ 3a(2)
= 2versch
+ 3,5
a
0
1
2
3
bij
a=0
Naam
Formule
Grafiek
Kenmerken
!!!!!!!!!!!!
+1
(1) verschil
in be
(3) versch
Naam
Formule verband
Tabel
Grafiek
Kenmerken
P
5 +1 8+1
11
14 Extra
verband
Naam
Formule
Grafiek
Kenmerken
Extra
(2)
verschil
st
a Tabel
0 +3 1 +3 2 +33
Altijd
rechte
REGELMAAT:
Som
(+) ofinvers
Prijs
= 5 + 3 x aantal
Lineair
Invullen
geeft:
AltijdInvullen
rechte lijn geeft:
REGELMAAT:
Som (+)
of verschil
(-) lijn
formule
Prijs = 5 + Lineair
3 x aantal
verband
(3)
verschil begiP
P Invullen
5 geeft:
8
111 stapje,
14
1 stapje,
verband
per
Formule
Formule
1
P = 5 + 3a
P = 5 + 3a
P = 5 +verband
3a Grafiektekenen
Lineair
Altijd rechte
lijn
REGELMAAT: per Som
(+) of verschil (-)
formule 1
Prijs = 5 + 3 x aantal
LETOP:
P = verband
5+3x0=5
telkens
Formule 2
P = 2 + 3,5a +
per 1 stapje,komt Formule
1
P = 5Formule
+ 3a Dus 2bij a=P
P = 5 + 3a
P = 5 + 3 x+3
0 = 5 +3komt er+3
er telkens
P=5+3x1=8
hetzelfde bij of af
Somformule S = 7 + 6,5a
komt er telkens
Formule
2 af P = 2Somformule
+ 3,5a
Altijdeenrechtelijn
5 ++ 3 x 6 =
P = 5 P+=35 x+ 31 x=0 8= 5•
hetzelfde
bij of
P = 5 + 3 x 2 = 11
begingetal stapgrootte
P=5+3x1=8
hetzelfde bij of af
Somformule S = Dus
7 + 6,5a
bij a=6 zijn
P = 5 begingetal
+ 3 x 3 = 14
Formule’s vergelijken
P = 5 P+=35 x+ 32 x=2 11
uitkomst
+ of - per
stapgrootte
= 11
begingetal
stapgrootte
•
Alsenigeeenrechtelijn
2
5Formule’s
+ 3 x 6 = 23
en
!!
5 + 3a = 2 + 3,5a
bij a=0
1 stapje
P = 5 P+=3geeft:
3 x=3 14
5x
+3
= 14
Formule’s vergelijken
verg
per
++1
of - per+ of -Grafiek
H uitkomst
= a +1
– 6a+1+uitkomst
9
Invullen
Maximum
SYMMETRISCH:
Naam
FormuleKwadratisch Tabel
Kenmerken
Extrain begingetal 5 – 2 = 3
!!!!!!!!!!!!
(1) verschil
5 + 3a = 2 + 3,5a 5 + 3a
bij1a=0
1 stapje
!! !!!!!!!!!!!!!!
= 2 + 3,5
verband
Minimum
verband
(2) verschil in stapgrootte 3,5 – 3 = 0,5
a bij 0a=0
1
2 stapje
3
2
Je
kunt
de
tabel
en
+1
+1
(1) verschil in begingetal 5 – 2 (hoog
=3
H =geeft:
+ 9 14
Invullen
2 geeft: +1
(3) verschil
begingetal
: verschil
stijggetal SYMMETRISCH: Maximum
POP
5a – 86a
Lineair
Invullen
Altijd
Som (+)
of verschil
(-) formule
Prijs = 5 + 3Kwadratisch
x aantal
!!!!!!!!!!!!
+1 3
(1) verschil
b
ELKE
“a” 11
VUL JE
H
=rechte
1 –alijn6 x +1
1 + 91+1
= 4 REGELMAAT:
de
(2) verschil
3,5 symme
–(laags
3 =in
0,5
0
2
grafiekin stapgrootte
Formulemaken
Uitkomst=begingetal+/-stijggetalxinvult
verband
Minimum
3P: 0,5
+3
+3
+3
verband
Formule 1
= 5 =+ 63a
P = 5 + 3a
Je kunt de
tabel en
(2): verschil
verschil
in s
a222 –P 60 x 52 +198= 1 11
2per 114stapje,
3
(3) verschil
begingetal
stijgget
TELKENS
HETZELFDE
H
=
“dubbelvouwen”
via
P = 5OP
+ 3 xELKE
0 = 5 “a” VUL JE
er telkens
Formule 2
P = 2 + 3,5a +
H = 1 2– 6 x 1 ++3
9 = 4+3 komt
de
symmetrie-as
grafiek
3
:
0,5
=
6
+3
(3) verschil
(uitkomstbij0)(wat+/–per1stapje)
P2
5
8
11
14
Dus bij a=6 zijn ze gelijk,
--------!
Afstandbeg
lin
P = GETAL
5TELKENS
+ 3 x 1 =IN
8 HETZELFDE
S =controleren:
7 + 6,5a
de symmetrie-as
HH==232––66xx23+ +9 9= =1 0hetzelfde bij of af5 + 3 xSomformule
“dubbelvouwen”
via
6 = 23 en 2 + 3,5 x 6 = 23
+3
+3
+3
P = 5 + 3 x 2 = 11
2
begingetal stapgrootte
gelijk
Dus bij a=6 zijn zeAfstand
gelijk, controleren:
HH==342––66xx34+ +9 9= =0 1
linksaan
va
Formule’svergelijken
5+3xa=12+2xa
de
symmetrie-as
P = 5GETAL
+ 3 x 3 = IN
14 --------!
Formule’s
vergelijken
uitkomst2
+ of - per
5 + 3 x 6 = 23 en 2 + 3,5 xsymmetrie
6 = 23
2
=1 4
Kwadratisch
H = a – 6a + 9
Invullen geeft:
Maximum (hoogste punt) of
HH==45 ––66xx45+ +9 9=SYMMETRISCH:
gelijk
aana=6
afstan
!!
5 + (laagste
3a = 2 +punt)
3,5aliggen altijd op
bij a=0
1 stapje
Dus bij
zijn
verband
Minimum
2
de tabel en
Kwadratischverband
Formuleinvullen
a=2
2
2
!!!!!!!!!!!!
(1) verschil in begingetal
5–2=3
H! = 5 Invullen
– 6 x 5geeft:
+ 9 =Je4kuntgrafiek
a – 6a + 9
Maximum (hoogstesymmetrie-as
punt)
of
OP ELKE “a” VUL JE
H = Kwadratisch
1 – 6 x +1
1 + 9 =+14 H = +1
de symmetrie-as
SYMMETRISCH:
5 + 3 x 6 = 23 e
2
2
2
(2)
verschil
in
stapgrootte
3,5
–
3
=
0,5
a
0
1
2
3
verband
Minimum
(laagste
punt)
liggen
altijd
op
TELKENS HETZELFDE
H=2 –6x2+9=1
H=a –6a+9
Naam
verband
Lineair
verband
+ of - per
1 stapje
H=2
+6x2+9=1
!
Je kunt de tabel en
“dubbelvouwen” via
!
2
2
(3)links
verschil
begingetal
: verschil
stijggetal
8 = 0 OP
11 ELKE
14“a” VUL JE
H = 1 – 6 x 1 + 9 de
= 4symmetrie-as
de symmetrie-as
GETAL IN --------!
HP
= 3 – 65 x 3 + 9
Afstand
van de
symmetrie-as
is grafiek
2
2
: “dubbelvouwen”
0,5 = 6
a H = geeft:
122 – 6 x 22 + 9Kenmerken
4
5gelijk
! Invullen
H = 4 H– =
6 xa
4 +–9 6a
=+3
1 TELKENS
aan afstand rechts van3de
+3
= 13
Kwadratisch
+ 9+3 HETZELFDE
Maximum (hoo
Formule
Tabel
Grafiek
Extra
via
2
2
H
=
5
–
6
x
5
+
9
=
4
symmetrie-as
GETAL
IN
--------!
H
=
3
–
6
x
3
+
9
=
0
Afstand links van deMinimum
symmetrie-as
is
de
symmetrie-as
verband
(laag
aH
142 2 1
30 4 1 5 4
de tabel
en
Dus
bijverschil
a=6 zijn(-)zeformule
gelijk, controleren:Je kuntgelijk
1
aan afstand rechts van de
2lijn= 4 – 6 x 4 + 9 =REGELMAAT:
!
Invullen
geeft:
Altijd rechte H
Som
(+)
of
Prijs = 5 + 3 x aantal
OP ELKE “a” VUL JE
HH= 1H –=4562 x– 611x+5 9+ 9=0
44
de symmetrie-a
1stapje, 4 Formule
grafiek
5
+
3
x
6
=
23
en
2
+
3,5
x
6
=
23
=
symmetrie-as
per
1
1
P
=
5
+
3a
P = 5 + 3a
!
2
HETZELFDE
H = 2! – 6 x 2 + 9 = 1
P = a5 +TELKENS
3 1x 0 = 2
5
komt er telkens
“dubbelvouwen” via
Formule 2
P = 2 + 3,5a +
3
4
5
2
2
H = a – 6a + 9
Maximum S(hoogste
punt) of
PInvullen
= H5 +GETAL
3 geeft:
8 IN 0 --------!
bij of af
Somformule
= 7 + 6,5a
H = 3! – 6 x 3 + 9 =hetzelfde
0SYMMETRISCH:
Afstand links va
4x 1 = 1
1
4
de symmetrie-as
2
Minimum
(laagste
punt)
liggen
altijd
op
P = 5 + 3 x 2 = 11
begingetal stapgrootte
Je
kunt
de
tabel
en
H = 4 –a 6 x 14 + 92 = 13
gelijk aan afsta
4
5
2
PH==51+ –3 6
x3
Formule’s
vergelijken
OP
ELKE “a”+VUL
JE
x=
1 14
+9=4
de symmetrie-as
uitkomst
of - per
2 H
grafiek
Uitkomst g
4
1
0
1
4
2
H=5 –6x5+9=4
symmetrie-as
!!H = 2 – 6 x 2 + 9 = 1
bij a=0
1 stapje
TELKENS
HETZELFDE
“dubbelvouwen” via5 + 3a = 2 + 3,5a
Uitkomst
gegeve
2
invullen
->
!!!!!!!!!!!!
(1) verschil
inlinks
begingetal
5 – 2 je
=3
GETAL IN --------!
H = 3 – 6 x+1
3 + 9+1= 0 +1
Afstand
van wat
de symmetrie-as
is
de
symmetrie-as
Uitkomst
gegeven
maar
moet
invullen
-> INKL
2
(2) verschil
in stapgrootte
3,5 van
– 3 =de
0,5
3
H a= 4 – 06 x 4 +1 9 = 12
gelijk
aan
afstand rechts
invullen
-> INKLEMMEN
2
(3) verschil
begingetal : verschil stijggetal
14
HP
=H
5 =
– 56√4a
x 5 +8 9 = 411
symmetrie-as
Wortel
Invullen geeft:
HAAKJES:
Uitkomst
gegeven maar wat moet je
3 : 0,5 = 6
+3
+3
+3
a
1
2
3
4
5
H =geeft:
√4a
Invullen
geeft:
HAAKJES:
H = √4a Wortel
! Invullen
verband
H = √(4 x 0) = 0 ZetHAAKJES:
Zetinvullen
de berekening
-> INKLEMMEN
H
=
√(4
x
0)
=
0
de
berekening
verband
H =H√(4 x 40) = 01
Zet de berekening
0
1
4 Dus bij a=6 zijn ze gelijk, controleren:
!
H = √(4 x 1) = 2
H = √(4 x 1) = 2 onder het wortelonder het wortela √(4 x1 2) = 2,8
2
3H = √4a
4
5
H = √(4Invullen
x 1) =geeft:
2
onder het wortel5 + 3 x 6 = 23 en 2 + 3,5 x 6 = 23HAAKJES:
H = Wortel
teken tussen
√(4
2,8
tussen
1
0
1
4
Hx
=x√(4
x=
0)
=0
Zet de berekening
HH==√(4
2)2)=
2,8
tekenteken
tussen
HH= verband
√(4 x4 3) = 3,5
haakjes
2
H = a – 6a + 9
Invullen
H =x√(4
x=
1) 3,5
= 2 SYMMETRISCH: Maximum (hoogste punt) of onder het wortel√(4
haakjes
H = √(4geeft:
x 4) = 4
HH==√(4
x= √(4
3)3)=
3,5
haakjes
Minimum
(laagste
punt)
liggen
altijd
op
H
x
2)
=
2,8
teken
tussen
√(4xx4)4)==4 4 Je kunt de tabel en
2
19=4
2
3
4
HH==√(4
OP ELKE “a” VUL JE
H =a 1 – 06 x 1 +
de symmetrie-as
H = √(4 x 3) = 3,5
haakjes
grafiek
Uitkomst gegev
2
2 9 =2,8
3,5
4
TELKENS HETZELFDE
H =H 2 – 06 x 2 +
1
H =0√(4 x 4)1= 4 “dubbelvouwen”
a
2 3 3 4via4 Afstand
Naam
Formule
Tabel
Grafiek
Kenmerken
Extra
2
Uitkomst
gegeven maar wat moet je
a
0
1
2de
invullen -> INK
GETAL IN --------!
H=3 –6x3+9=0
links van de symmetrie-as is
symmetrie-as
a0 0 2 1 2,8
2
33,5 4 4
2
-> INKLEMMEN
Verband
H=4 –6x4+9=1
gelijkinvullen
aan afstand
rechts van de
HH
0
2 2 2,82,8
3,5
4
2
H
0
3,5
4
H = 5Altijd
– 6 x 53+formules:
symmetrie-as
Hyperbolisch
LInvullen
invullengeeft:
in de formule
OMGEKEERD
Het gedeelte va
Wortel
H
= √4a9 = 4
HAAKJES:
H = √4a
HAAKJES:
!Invullen geeft:
verband
BH==10
: Lx 0) = 0
EVENREDIG:
relevant is:
Naam
Tabel
Kenmerken
verband H = Formule
√(4
Zet
de berekening Extra
√(4 x 0) = 0
Zet de berekening Grafiek
!
Boven
2
bedenk wat binn
• xL
B = 10
H = √(4
1) x
=2
onder het wortelVerband
H = √(4 x 1) = 2
onder
het xwortela
1
2
3
4
5
√(4
2)
2,8
teken tussen
==10
: 1xin=2)de
10
geeft
werkelijkheid
ka
• xL
10 : B 1
HyperbolischHH= Altijd
3==formules:
LBH
invullen
OMGEKEERD
Het
gedeelte va
√(4
= formule
2,8
teken
tussen
4
H = √(4 4x 3) =13,5 0
haakjes
10
Onder
:2
LET OP:is:
de gra
• xB
= 410 : L
verband
BBH
===
10
::L2x =3)5= 3,5
EVENREDIG:
relevant
√(4
haakjes
H = √(4
4) =
Tabelinvullen
SYMMETRISCH:
Of
!
!
Wortel
verband
Minimumenmaximum
MinimumMaximum
(laagstepunt)(hoogstepunt)
Kwadratisch
Symmetrie
• Uitkomstenintabelengrafiekkunjedubbelvouwen
verband
viadesymmetrie-asàstippellijn
• Hoogsteenlaagtepuntligtaltijdopdesymmetrie-as
Wortel
• Afstandlinks/rechtstussensymmetrie-asengrafiekishetzelfde
verband
Wortelverband
Formuleinvullen
a=3enrondafop1decimaal
H=√4a
H=√(4x3)=3,5
B = 10 : 3x =4)3,3
lijn kleuren
Boven x 2
bedenk
wat die
binnj
• 0 L x 1B = 10
=4
Tabelinvullen
H =10√(4
a
2
3
4
2,5
x2 x2
via 3,5 4
BB==10
::14==10
geeft
werkelijkheid ka
B
H •Onthouden
0 L = 210 :2,8
Uitkomst
gegeven
maar
wat
moet
je
a
0
1
2
3
4
L Onder
1
2
B! = 10 : 2 = 5
:2 4
LET OP: de gra
• B = 10 : L
invullen -> INKLEMMEN
44
B 10 5 2,4
B =HL10 : 30 =1 3,32 2 2,8 33,5
lijn kleuren die je
3,3
2,5
Wortel
H = √4a
Invullen
geeft:
HAAKJES:
:x2
2 :x2
2
10via
B = B10 : 4 10
= 2,5 5
Onthouden
verband
H = √(4 x 0) = 0
Zet de berekening
!
L
1
2
4
Grafiektekenen
H = √(4 x 1) = 2
onder het wortelLet
Naam
Formule
Tabel
Grafiek
Extra
L x B
L
1
2 Kenmerken
3 tussen4
B op:10werkt
5 ook
2,4
H = √(4 x 2) = 2,8
teken
Verband
met x3, x4,
etc.
H = √(4 x 3) = 3,510
haakjes 2,5
B
10
5
3,3
: 2 x5: 2
Hyperbolisch Altijd 3 formules:
L invullen
inxde
OMGEKEERD
Het gedeelte van de grafiek kleuren dat
H = √(4
4) formule
=4
verband
B = 10a : L 0
EVENREDIG:
relevant
is:
1
3
4
op: werkt ook
L x2 B3,5
t
Boven x 2
bedenk wat binnen het verhaalLet
in de
• L x B = 10 ExponentieelH Aantal
0
2= 32,8
4
Invullen geeft:
x 1,5
GROEIFACTOR
B = 10 : 1 = 10
geeft
werkelijkheid kan voorkomen. met x3, x4, x5 etc.
• L = 10 : B
verband B = 10 : 2 = 5
Onder
:
2
LET
OP:
de
grafiek
kleuren
betekent
de
• B = 10 : L
Exponentieelverband
Formuleinvullen
t=2enrondafop2decimalen
Aantal = 3 x 1,5
^0 = 3
+1
B = 10 : 3 = 3,3
lijn kleuren die je zelf hebt getekend. +1
t
2
Groeifactor!
Aantal =geeft:
3 x 1,5=6,75
^1 = 4,5
B = 10 : Aantal
4Begin= 2,5 = 3 x 1,5t Groeix2 x2
t 0
1
2
A=3x1,5 Onthouden via Exponentieel
A=3x1,5
Invullen
GROEIFACTOR
!
L
1
2
4
2 A 3 4,5 6,75
hoeveelheid
factor
Aantal = 3 x 1,5 ^2 = 6,75
verband
LETOP:niet“1,5x2”maar“totdemacht2”à
1,5
L
1
2
3
4
B 10 5 2,4
Aantal==33xx1,5
1,5^0
^3==310,125
x1,5 +1
x1,5
Aantal
+1
B
10
5
3,3
2,5
:2 :2
10
Groeifactor!
Tabelinvullen
BeginGroeiAantal = 3 x 1,5 ^1 = 4,5
t 0
1
2
Hoeve
t
0
1
2
3
Formule
Tabel
Grafiek
Extra
hoeveelheid Kenmerken
factor
Aantal
^2 = 6,75
Let op: werkt ook
L x B
A 3 4,5 NIEUW
6,75
A = 33x 1,54,5
6,75
10,125
groeifactor = OUD
met
x3,dat
x4, x5 etc.
Aantal
= 3 xvan
1,5
= 10,125
x1,5 x1,5
Altijd 3 formules:
L invullen in de formule
OMGEKEERD
Het gedeelte
de^3
grafiek
kleuren
Groeifactor is 1
berekenen
relevant is:
B = 10 : L
EVENREDIG:
Boven x 2
bedenk wat binnen het verhaal in de
4,5 : 3 = 1,5x
• L x B = 10
Hoeve
0 kan voorkomen.
1
2GROEIFACTOR
3
NIEUW
Invullen geeft:
B = 10 : Aantal
1 = 10 = 3 x 1,5
geeft
Grafiektekenen
twerkelijkheid
• L = 10 : B Exponentieel
De groei is d
6,75 : 4,5 = 1,5x
A
3 grafiek4,5
Onder : 2
LET OP: de
kleuren6,75
betekent10,125
de
groeifactor = OUD
x 100
• B = 10 : L verband B = 10 : 2 = 5
B = 10 : 3 = 3,3
lijn
kleuren
die
je
zelf
hebt
getekend.
Groeifactor is 1
Aantal = 3 x 1,5 ^0 = 3
+1
+1
berekenen
B = 10 : 4 = 2,5
x2 x2
Groeifactor!
Periodiek
Een gedeelte
komt
Als de periode 6
Procenten
!
Onthouden via
BeginGroeiAantal = 3 x 1,5 ^1 = 4,5
t 0
1
2
: 3 =Dit
1,5x
!
verband Aantal = 3 x 1,5 ^2 = 6,75L 1 2 4 of
telkens4,5
terug.
dan is de uitkom
hoeveelheid
factor
A
3
4,5
6,75
De groei is du
L
1
2
3
4
B 10 5 2,4
6,75 :we
4,5de
= 1,5x
noemen
weer hetzelfde.
Aantal = 3 x 1,5 ^3 = 10,125 : 2 : 2
: 100
x1,5 x1,5
B
10
5
3,3
2,5
10
periode.
Periodiek t
Een gedeelte komt
Als
6
Hoeveel % is de groei?
L x B
0
1
2Let op: werkt
3 ook
NIEUW
Dusde
0,periode
6, 12, 18
met x3,
x4, x5 etc.
verband A
telkens terug. Dit
dan
is de uitkom
uitkom
3
4,5 6,75
10,125
groeifactor = OUD
dezelfde
t
Groeifactor is 1,5 dus 1,5 x 100
= 150%we de
noemen
weer hetzelfde.
berekenen
Formulelezen
UItkomst=beginhoeveelheidxgroeifactor
4,5 : 3 = 1,5x
periode.
Aantal = 3 x 1,5
Invullen geeft:
GROEIFACTOR
Maar ook bij 2,
Groeifactorenprocenten
De groei is dus 150% - 100% = 50%
6,75 : 4,5 = 1,5x
x 100
Dus 0, 6, 12, 18
Aantal = 3 x 1,5 ^0 = 3
+1
+1
Groeifactor!
Procenten!
dezelfde uitkom
BeginGroeiAantal = 3 x 1,5 ^1 = 4,5
t 0
1
2
Periodiek
Een gedeelte komt
Als de periode 6 seconde is,
hoeveelheid
factor
Aantal = 3 x 1,5 ^2 = 6,75
A 3 4,5 6,75
verband
terug. Dit
dan is de uitkomst om de 6 seconde
MachtsGebruik ^ : 100 telkens
Aantal = 3 x 1,5 ^3 = 10,125
x1,5 x1,5
Maar ook bij 2, 8
noemen we de
weer hetzelfde.
verband
periode.
Hoeveel % is de groei?
t
0
1
2
NIEUW Dus1,5x100=150%of75%:100=0,75
! 3
Dus
0,
6,
12,
18,
24,
30
sec
hebben
A
3
4,5 6,75 10,125
groeifactor = OUD
!
dezelfde uitkomst
Groeifactor
berekenen
MachtsGebruik
^ is 1,5 dus 1,5 x 100 = 150%
4,5 : 3 = 1,5x
verband
De groei is dus 150% - 100% = 50%
6,75 : 4,5 = 1,5x Groeifactorhoudjeoverdus:150%-100%=+50%
Toe/afnameinprocenten
Maar ook bij 2, 8, 14, 20, 26, 32 sec
!
Een gedeelte komt Aantal=300+2,4xtmett=0op2010
Als de periode 6 seconde is,
Algemenevaardigheden
Rekenenmett=0op….
!
telkens terug. Dit
dan is de uitkomst om de 6 seconde
MachtsGebruik ^
noemen we de
weer hetzelfde.
t=10àjaartal2020jaartal2024àt=14
verband
periode.
Dus 0, 6, 12, 18, 24, 30 sec hebben
!
!
Inklemmen
Inwelkjaartalishetaantalvoorheteerstgroterdan400?
dezelfde uitkomst
300+2,4x41=398,4àuitkomstdichtseronder
Maar ook bij 2, 8, 14, 20, 26, 32 sec
<400
300+2,4x42=400,8àuitkomstdichtserboven
Gebruik ^
Dust=42àjaartal2052àdejuistekeuze
Kwadratisch
verband
Grafiektekenen
t
t
Rekenen
Handigrekenen
Schatten
Duizend,miljoenen
miljard
Afronden
Eenhedenomrekenen
ßLinks=DeLen
àRechts=Keer
Lengte
Oppervlakte
Inhoud
Gewicht
Tijd
Snelheid
Verhoudingen
De“1”staatnooitalleen
Procentenbegrippen
100%gegevenen
percentagegegeven
100%gegevenen
percentagegevraagd
100%gevraagden
percentagegegeven
Andereverhoudingen
GebruikTABEL
• 1man=1,80m
• 1verdieping=3m
• Nederlandheeftongeveer16500000inwoners
• Eenpersoonlooptongeveer5kmin1uur
• Eenpersoonfietstongeveer15kmin1uur
• overdeweg=1,2xhemelsbreedà
Duizend:3getallenachterdekomma3,5duizend=3500
Miljoen:6getallenachterdekomma4,25miljoen=4250000
Miljard:9getallenachterdekomma6,35miljard=6350000000
0,1,2,3,4àgetalervoorblijftgelijk
5,6,7,8,9àgetalervoor+1
Regelsookgewoongebruikenbijverplichtafrondenopeenheelgetalbij
bijvoorbeeldmensen,dierenetc.
LETOP:Bijeenberekeningmetmeerderestappentussendoor
nietafronden.Schrijfdetussenuitkomstopmet“5,46….”
engaverdermetdeheleuitkomstopjerekenmachine
LETOP:
3
1liter=1dm
3
1ml=1cm 1minuut=60seconden1uur=60minuten1dag=24uur
1jaar=365dagen1jaar=12maanden1jaar=52weken
5m/sx3,6=18km/uur
43,2km/uur:3,6=12m/s
100%=geheel,beginofexclusief
min….%àgoedkoper,korting,dalen,verminderenetc.
plus….%àduurder,verhoging,vermeerderen,groeienetc.
Inclusief=exclusief(100%)+btw(21%)=121%
Dus€500:100x15=€75
Dus100%:120x38=31,7%
Dus€14:121x100=€11,57
15kmperuurà15kmin1uur
Eenkroketkost€2à€2voor1kroket
Elkuurverdienje€5à€5in1uur
TegenAllesBerekenbaarEnLastig
Meetkunde
Aanzichten
Inhoud,oppervlakteen
omtrek
Uitslagen
Voor-,zij-en
bovenaanzichten
Doorsneden
Oppervlakterechthoek
Oppervlaktedriehoek
àofof
of
Lengtexbreedte
½xzijdexhoogte
Oppervlakte
Cirkel
Omtrekrechthoek
Omtrekdriehoek
Omtrekcirkel
Inhoudbalk,cilinderof
prisma
Inhoudkegel/piramide
Oppervlakteruimtefiguur
Eigenschappen
meetkundigefiguren
Driehoek
Allehoekensamen180°
Rechthoekigedriehoek
Gelijkbenigedriehoek
Gelijkzijdigedriehoek
Gestrektehoek
Overstaandehoeken
Symmetrie
Kortezijdeuitrekenen
Langezijdeuitrekenen
Toepasbaarheid
herkennen
1hoekis90°
(sinus,cosinus,tangensenpythagosmogelijk)
2zijdenen2hoekenzijnevengroot
1symmetrie-as
3zijdenen3hoeken(60°)evengroot
3symmetrie-assen
hoekendiesameneenrechtelijnvormenzijn
180°àhoekD2=180°-78°=102°
StellingvanPythagoras
(kort,kort,lang)
2
Straal xπ
L+L+B+B
zijde1+zijde2+zijde3
Diameterxπ
oppervlaktegrondvlakxhoogte
1
/3xoppervlaktegrondvlakxhoogte
optellenoppervlaktevanallezijvlakken
hoekendiesameneencirkelvormenzijn360°
bijeenkruiszijntegenovergesteldeevengroot
LijnsymmetrieDraaisymmetrieSchuifsymmetrie
DestellingvanPythagoraskunjealleenbijeen
rechthoekigedriehoekgebruiken
Goniometrie
(sinus,cosinus,tangens)
Hoekbepalen
Zijdenbenoemen
Sinus(SOL),
Cosinus(CAL)of
Tangens(TOA)kiezen
JekijktofLETOP:
àvanuitdehoekdiejewiltuitrekenenJekijktnooitvanuit
àvanuitdehoekdiejealweetderechtehoek
Streepdezijdewegdienietindeopgavevoorkomt
Jegebruiktdezijdewaarbij:
• Delengtebekendis
• Delengteberekendmoetwordenàhetvraagteken
BijTangens(TOA)àOenAkomeninopgavevoor
BijSinus(SOL)àOenLkomeninopgavevoor
BijCosinus(CAL)àAenLkomeninopgavevoor
Rekenen met de hoek, A en L
Rekenen met dehoek, O en A
Rekenen met de hoek, O en L
-1
-1
-1
HoekuitrekenenTan … = O : A Tan TOA
(O:A)Sin (O:L)Cos
(A:L)
CAL
Cosinus … = A : L
SOL
Sinus … = O : L
Zijdeuitrekenen
O
tan ..x A
O=tan(hoek)xAO=sin(hoek)xLA=cos(hoek)xL
=O:L
L = O : sin
sin
= A :OL= sin xLL = A : cos
A = cos x L
cos
=O:A
A = O : tan
O = tan x A
tan
A=O:tan(hoek)L=O:sin(hoek)L=A:cos(hoek)
Toepasbaarheid
Detangens,sinusencosinuskunjealleenbijeen
herkennen
rechthoekigedriehoekgebruiken
Jekuntweleenrechthoekigedriehoekmakendoorhulplijnen
àofà
Kijklijnen
Eenkijklijniseenrechtelijn
tussen2punten
Koersmeten
• Koerstekenentussen2punten
• Middenkoershoekmeteropvertrekpunt
• Noordpijlomhoog
• Getekendelijngeeftkoersaan
Hoekmeten
• Middenkoershoekmeteroppunt
• Noordpijl(0graden)oplinkerbeen
• Rechterbeengeeftaantalgradenaan
Schaalrekenen
1:200000à1cmopdekaartis200000cminhetecht
LETOP:
Eenschaalzondereenheid
staatisditaltijdinCM
Schaallijn
à
Schaaluitrekenen
lengteinhetecht:lengteopdekaart
LETOP:lengtesmoetenwelindezelfdeeenheidstaan
àbijvoorbeeldbeideincm
© Thijs de Corte
© Thijs de Corte
© Thijs de Corte
Losseonderdelen