Afstanden berekenen met meetrollen

Afstanden berekenen met meetrollen
Zwaluwstaartpassingen worden niet alleen in houten constructies gebruikt, maar
ook voor het aaneenzetten van metalen onderdelen. Correcte afmetingen zijn
daarbij essentieel.
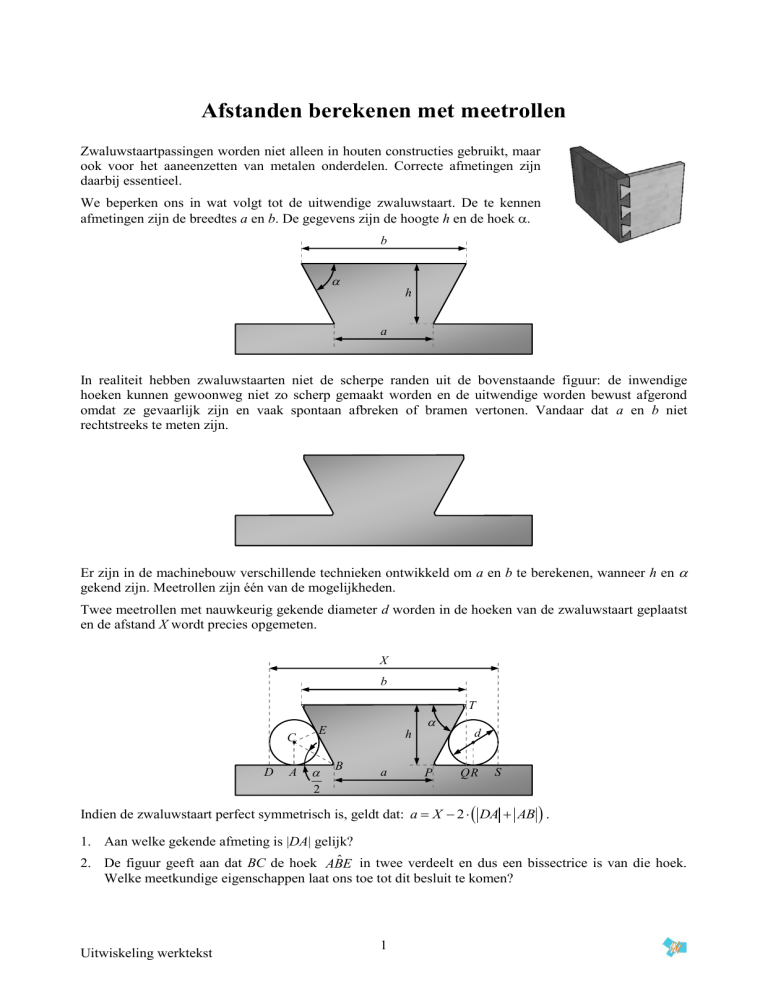
We beperken ons in wat volgt tot de uitwendige zwaluwstaart. De te kennen
afmetingen zijn de breedtes a en b. De gegevens zijn de hoogte h en de hoek .
b

h
a
In realiteit hebben zwaluwstaarten niet de scherpe randen uit de bovenstaande figuur: de inwendige
hoeken kunnen gewoonweg niet zo scherp gemaakt worden en de uitwendige worden bewust afgerond
omdat ze gevaarlijk zijn en vaak spontaan afbreken of bramen vertonen. Vandaar dat a en b niet
rechtstreeks te meten zijn.
Er zijn in de machinebouw verschillende technieken ontwikkeld om a en b te berekenen, wanneer h en 
gekend zijn. Meetrollen zijn één van de mogelijkheden.
Twee meetrollen met nauwkeurig gekende diameter d worden in de hoeken van de zwaluwstaart geplaatst
en de afstand X wordt precies opgemeten.
X
b
T
C
D
A

E

h
B
a
P
d
QR
S
2
Indien de zwaluwstaart perfect symmetrisch is, geldt dat: a  X  2   DA  AB  .
1. Aan welke gekende afmeting is |DA| gelijk?
ˆ in twee verdeelt en dus een bissectrice is van die hoek.
2. De figuur geeft aan dat BC de hoek ABE
Welke meetkundige eigenschappen laat ons toe tot dit besluit te komen?
Uitwiskeling werktekst
1
3. In de driehoek ABC zijn de zijde AC 
d
ˆ   gekend. Gebruik deze gegevens om
en de hoek ABC
2
2
|AB| te berekenen.
4. Leid uit de antwoorden op de vorige vragen een formule af voor a waarin enkel de gekende
afmetingen X, d en  voorkomen.
Nu a gekend is, kan hieruit vervolgens b berekend worden. Op de figuur zie je immers dat b  a  2  PQ .
5. Met behulp van de formules voor rechthoekige driehoeken is het mogelijk om een formule voor |PQ|
te vinden, die enkel gebruik maakt van de gekende afmetingen X, h,  en a. Stel die formule op.
6. Gebruik je antwoorden op vragen 4 en 5 om de volgende formule aan te tonen:


1
b  X  d 1 
 tan 
2

Uitwiskeling werktekst
2


2h
.

 tan 
