Hoofdstuk 4 Het schakelen van weerstanden.

Elektriciteit
Hoofdstuk 4 Het schakelen van weerstanden.
1.
Doel.
Het is de bedoeling een “grote” schakeling met weerstanden te vervangen door één
equivalente weerstand. Een equivalente schakeling betekent dat een buitenstaander
(dit kan bv. een ohmmeter of een andere schakeling zijn) geen verschil merkt tussen
de oorspronkelijke schakeling en de equivalente schakeling.
2.
Theoretische achtergrond voor het schakelen van weerstanden.
2.1.
Serieschakeling.
Beide schakelingen zijn equivalent als een buitenstaander geen
verschil ziet tussen beide schakelingen. Bij het aanleggen van
dezelfde spanning (U), moet er naar beide schakelingen dezelfde
stroom (I) vloeien.
In een serieschakeling vloeit er door elke weerstand dezelfde
stroom (I=I1=I2=…=In).
Rs 
U Us R1* I1  R 2 * I 2  ...  Rn * In R1 * I  R 2 * I  ...  Rn * I



 R1  R 2  ...  Rn
I
I
I
I
Rs  R1  R 2  ...  Rn
2.1.1. Merk op:
Rs is steeds groter dan de grootste.
Als alle weerstanden gelijk zijn dan Rs  n * R en is er over elke
weerstand dezelfde spanning.
Over de grootste weerstand staat de grootste spanning.
Over de kleinste weerstand staat de kleinste spanning.
Als er tussen 2 weerstanden een knooppunt is, dan staan de 2
weerstanden NIET in serie. Waarom?
KHBO
4.1
Elektriciteit
2.2.
Parallelschakeling
I1
R1
R1*I1
I2
R2
R2*I2
In
Rn
Rp
Rn*In
Up
I
I
U
A
U
B
A
B
Over elke weerstand die in parallel staat, staat dezelfde
spanning
(U= U1=U2=…=Un).
Up U
U
 
I
I I1  I 2  ...  In
1
1
1
I1  I 2  ...In I1 I 2
In I1 I 2
In
1

 
 ...  

 ... 


 ... 
Rp
U
U U
U U1 U 2
Un R1 R 2
Rn
Rp 
1
1
1
1


 ... 
Rp R1 R 2
Rn
1 1
1
1
1 1
( )  Rp  ( 
 ... 
)
Rp
R1 R 2
Rn
2.2.1. Merk op:
Als er 2 weerstanden in parallel zijn (R1 en R2) dan geldt:
Rp  (
KHBO
R2
R1 1 R1  R 2 1 R1* R 2
1
1 1


) 
) (
) (
R1 R 2
R1 * R 2 R1* R 2
R1* R 2
R1  R 2
4.2
Elektriciteit
Rp 
R1* R 2
R1  R 2
Deze formule is NIET geldig voor 3 of meer weerstanden in parallel!
Deze formule niet gebruiken met het rekentoestel (= meer werk).
1
Gebruik de algemene formule met je rekentoestel (  R 1 dus R
R
1
intypen gevolgd door de toets x ).
Het resultaat is steeds kleiner dan de kleinste.
Als er n gelijke weerstanden R in parallel staan, dan is Rp 
R
.
n
Door de kleinste weerstand vloeit de grootste stroom.
Door de grootste weerstand vloeit de kleinste stroom.
R
A
RAB  (
B
1
1
1 1 1
 )  (  ) 1  () 1   0
R 0
R

Ook hier is de vervangingsweerstand kleiner dan de kleinste.
Negatieve weerstanden bestaan niet. Als een weerstand kortgesloten is,
dan is de vervangingsweerstand steeds nul.
KHBO
4.3
Elektriciteit
2.3.
Ster- driehoek transformatie.
Soms gebeurt het dat er geen weerstanden in serie of parallel
staan.
Kijk dan als ze niet in ster of in driehoek staan.
De ster is vervangbaar door een equivalente driehoek en
omgekeerd.
Hoe?
2.3.1. Van driehoek naar ster.
Gegeven: a, b, c
Gevraagd: α, β, γ? Dus 3 onbekenden. Om dat op te lossen hebben we 3
onafhankelijke vergelijkingen nodig.
Oplossing:
Om die vergelijkingen te vinden beschouwen we volgende schakeling:
C
B los
B los
C
a
I
X
c
b
E
A
KHBO
E
A
4.4
Elektriciteit
In ster:
De stroom I zal enkel bepaald worden door de weerstanden α en γ.
β speelt hierin geen invloed daar deze weerstand los hangt.
α en γ staan bijgevolg in serie.
De stroom
I
E
E

RAC   
In driehoek:
De stroom I zal zich in C opsplitsen in een stroom door a en een stroom
door b. a en c staan in serie. Deze serieschakeling staat op zijn beurt in
parallel met b.
De stroom
I
E
E

(a  c) // b (a  c) * b
(a  c)  b
Beide stromen zijn slechts gelijk als de noemers gelijk zijn. Dus als RAC
ster = RAC driehoek
Of als RAC     
(a  c) * b
.
(a  c)  b
Op dezelfde wijze vindt men de 2 andere vergelijkingen die moeten
kloppen voor onze beide schakelingen.
RBA     
(b  a) * c
(2)
(b  a)  c
RCB     
(c  b) * a
(3)
(c  b )  a
R AC     
(a  c) * b
(1)
(a  c)  b
Om de sterweerstanden te vinden, kan men de ene formule
substitueren in de andere (= veel werk).
Het is echter mogelijk om de vergelijking snel op te lossen. Dat gebeurt
als volgt:
We voeren dezelfde bewerking (1)+(2)-(3) uit op het linker en het
rechter lid. Daardoor blijven deze leden in evenwicht:
Voor het linker lid:
(α+γ) +(β+α)-(γ+β) =2*α
KHBO
4.5
Elektriciteit
Voor het rechter lid:
(a  c) * b (b  a) * c (c  b) * a ab  cb  bc  ac  (ca  ba)
2bc




(a  c)  b (b  a)  c (c  b)  a
abc
abc
2 
2bc
abc



bc
abc
(4)
Wie goed kijkt ontdekt een wetmatigheid in het stelsel (1), (2) en (3).
KHBO
4.6
Elektriciteit
Men spreekt van cyclische formules.
Het resultaat van de berekeningen zal ook deze wetmatigheid volgen.
Zo kan men vlug de andere formules afleiden…
ca
ca

bca abc

ab
ab


bca abc
(5)
(6)
In woorden: de gezochte sterweerstand is het product van de
aanliggende driehoeksweerstanden gedeeld door de som van de
driehoeksweerstanden.
De aanliggende driehoeksweerstanden zijn de 2 weerstanden die
hangen aan hetzelfde punt als de gezochte sterweerstand.
2.3.2. Van ster naar driehoek.
Om vlug deze formules af te leiden start men best van de vergelijking
(4), (5) en (6).
(4) * (5)
(5) * (6)
( 6) * ( 4)
bc * ca
(a  b  c)²
ca * ab
 * 
Merk op: ook hier cyclische formules.
(a  b  c)²
ab * bc
 * 
(a  b  c)²
 * 
We tellen deze vergelijkingen op:
     
en
KHBO
abc
abc
bcca  caab  abbc abc(c  a  b)
abc


abc
(a  b  c)²
(a  b  c)²
bc
 a *       
abc
ac
b
 b *       
abc
ab
 c *       
c
abc
a
4.7
Elektriciteit
    
a

    
b

    
c

Merk op: ook hier cyclische formules.
In woorden: men vindt de driehoeksweerstand door de som van alle
producten van de sterweerstanden te delen door de overstaande
sterweerstand.
De overstaande sterweerstand is de sterweerstand die NIET hangt aan
de punten waar de gezochte driehoeksweerstand hangt.
3.
Werkwijze.
3.1.
Nummeren van de knopen.
Om een oefening tot een goed einde te brengen is het van groot
belang de knooppunten correct te nummeren.
Beschouw als knooppunt enkel de punten van de schakeling
waartussen je het equivalent zoekt en de punten van de
schakeling waarin minstens drie geleiders toekomen.
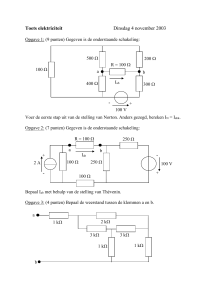
Voorbeeld: zoek, in figuur 1, de equivalente weerstand tussen A
en C.
R1
R2
A
B
C
R3
F
E
R4
R5
D
Figuur 1
KHBO
4.8
Elektriciteit
Je zoekt het equivalent tussen het punt A en het punt C: A en C
worden automatisch knooppunten. Om dit niet te vergeten, doe
je er goed aan de verbinding met de buitenwereld aan te duiden
op de tekening (zie figuur 2). In het punt D en F komen slechts 2
geleiders toe: D en F zijn geen knooppunten! Laat D en F
verdwijnen. B en E zijn wel knooppunten, ze blijven op de
tekening staan.
Je bekomt de volgende schakeling:
R1
R2
A
B
C
R3
R5
R4
E
Figuur 2
Alle punten die onderling verbonden worden met dezelfde
geleider, zullen steeds op hetzelfde potentiaal (elektrisch niveau)
staan. Beschouw al deze punten als hetzelfde knooppunt.
In figuur1 was dit het geval voor de punten A, F en E.
In figuur2 was dit nog enkel het geval voor de punten A en E.
Laat bv. E verdwijnen.
Bij tamelijk ingewikkelde opgaven kan het zelfs nuttig zijn de
opgave te hertekenen. Met de schakeling uit figuur 2 is dat niet
echt noodzakelijk.
Je bekomt de volgende schakeling (herteken desnoods zelf de
opgave):
R1
R2
A
B
C
R3
R5
R4
Figuur 3
Nu zijn alle knooppunten correct genummerd.
3.2.
Vereenvoudigen van de schakeling.
Zoek achtereenvolgens de hieronder besproken schakelingen op
en vereenvoudig de schakeling geleidelijk aan. Tijdens het
vereenvoudigen zullen de knoppunten een voor een verdwijnen.
KHBO
4.9
Elektriciteit
Let echter op: 2 knopen mogen nooit verdwijnen nl. de knopen
die de verbinding maken met de buitenwereld! (hier A en C)
3.2.1. Serieschakelingen
Zoek alle serieschakelingen in de schakeling op en vervang ze door
hun equivalente schakeling. Ter herinnering: twee of meer
weerstanden staan in serie als het einde van de ene weerstand hangt
aan het begin van de andere weerstand en als deze verbinding geen
knooppunt is. Door beide weerstanden zal steeds dezelfde stroom
vloeien.
In figuur 3 staan R4 en R5 in serie. R2 en R4 evenals R1 en R3 staan
niet in serie vermits er tussen de 2 weerstanden een knooppunt is (C,
voor de eerste 2; B en/of A voor de 2 andere).
Vervang je de serieschakeling, dan bekom je de volgende
vereenvoudigde schakeling:
R1
R2
A
B
C
R3
R45
Figuur 4
KHBO
4.10
Elektriciteit
Merk op: het knooppunt D is verdwenen.
3.2.2. Parallelschakelingen.
Zijn er geen serieschakelingen meer, dan zoek je of er
parallelschakelingen zijn.
Twee of meer weerstanden staan in parallel als ze beginnen in
hetzelfde knooppunt en eindigen in een (ander) zelfde knooppunt.
Na het vervangen van de parallelschakeling, begin je terug van vooraf
aan: 3.2.1 zoek of er nieuwe serieschakelingen ontstaan enz.
Naarmate je meer getraind bent in het maken van oefeningen, kan je de
serie- en de parallelschakelingen samen opzoeken en vervangen.
Passen we dit toe op de opgave dan zien we dat R3 en R2 niet in
parallel staan: ze beginnen wel in hetzelfde knooppunt (B), maar
eindigen in verschillende knooppunten (C en E).
Enkel R1 en R3 staan in parallel tussen de punten A en B. Na het
vervangen bekom je volgende schakeling:
R13
R2
A
B
C
R45
Figuur 5
In deze schakeling staan er geen weerstanden meer in parallel. We
keren terug naar 3.2.1 en zoeken of er nieuwe serieschakelingen
ontstaan. Dit is het geval voor R13 en R2. Na het vervangen bekom je
de volgende schakeling:
R12
A
C
R45
Figuur 6
Merk op: het knooppunt B is verdwenen.
In deze schakeling staan er geen weerstanden meer in serie. We
zoeken of er opnieuw parallelschakelingen zijn ontstaan. Inderdaad,
R12 staat in parallel met R45. Na het vervangen houden we nog slechts
KHBO
4.11
Elektriciteit
1 weerstand over, de equivalente schakeling:
R15
A
C
Figuur 7
3.2.3. Ster- driehoek transformatie
In een aantal uitzonderlijke gevallen kan het gebeuren dat er geen
serie- noch parallelschakelingen meer in de schakeling voorkomen en
dat de schakeling nog niet herleidt os tot 1 weerstand. Dan moet je op
zoek naar weerstanden die in ster (3 weerstanden die in hetzelfde punt
toekomen) of in driehoek (3 weerstanden vormen samen een lus en
tussen elke weerstand is telkens een knooppunt aanwezig) geschakeld
zijn. Je moet dan de ster vervangen door een equivalente
driehoeksschakeling of omgekeerd. Welke transformatie je ook doet,
het moet steeds leiden tot een nieuwe schakeling waarin opnieuw
serie- of parallelschakelingen in staan. Is dit niet het geval, kies dan
een andere schakeling en probeer het opnieuw. Na het vervangen
begin je opnieuw van vooraf aan: 3.2.1 serieschakelingen, 3.2.2
parallelschakelingen, enz.
Vervang nooit een ster of een driehoeksschakeling als er nog serieof parallelschakelingen in staan. Dit zou de vereenvoudiging enkel
moeilijker, langdradiger maken. In figuur 1 had je kunnen opmerken
dat R1, R2 en R3 in ster stonden. Mocht je ze vervangen hebben, dan
zou je hetzelfde eindresultaat bekomen, maar de weg zou langer
geweest zijn dan de oplossing die hierboven werd uitgewerkt. Probeer
dit maar eens.
KHBO
4.12
Elektriciteit
4.
Voorbeelden:
4.1.
Welke stappen moet je uitvoeren om de weerstand tussen A en B te
bepalen?
4.1.1. Oplossing:
R3 en R4 staan in parallel.
R1 en R34 staan in serie.
R14 en R2 staan opnieuw in parallel.
KHBO
4.13
Elektriciteit
4.2.
Welke stappen moet je uitvoeren om de weerstand tussen A en B te
bepalen?
4.2.1. Oplossing:
A en D zijn hetzelfde punt. Het heeft geen zin om een nieuwe naam te
geven aan dat punt. Herteken de schakeling, zonder dat D nog
voorkomt. Wat vroeger verbonden was met D wordt nu verbonden
met A.
R1 en R2 staan in parallel. R3 is op zichzelf kortgesloten en zal nooit
invloed hebben op de schakeling.
R12 staat nu in serie met R4.
KHBO
4.14
Elektriciteit
R14 staat nu in parallel met R5.
4.3.
Welke stappen moet je uitvoeren om de weerstand tussen A en B te
bepalen?
4.3.1. Oplossing:
Vermits C en F geen knooppunt zijn (hangen los) staan R2, R5 en R7 in
serie tussen B en E.
A
B
R1
R4
R3
R257
R6
E
R4 en R257 staan in parallel.
R3, R6 en R4-7 staan in serie. Bemerk dat je R3 en R6 reeds vroeger had
kunnen vervangen door een serie-equivalent. Dat equivalent zou dan
nu in serie staan met R4-7.
KHBO
4.15
Elektriciteit
A
B
R1
R3-7
R1 en R3-7 staan in parallel.
4.4.
Welke stappen moet je uitvoeren om de weerstand tussen C en D te
bepalen?
4.4.1. Oplossing:
Vermits A en F geen knooppunten zijn (los) staan R1 en R3
evenals R5 en R7 in serie.
Nu staat geen enkele weerstand nog in serie of in parallel
(Controleer!)
Wie bvb R2 en R57 zou vervangen door een serie-equivalent,
zou het knooppunt C verliezen. Daardoor wordt het onmogelijk
om nog de weerstand tussen C en D te zoeken!
We moeten dan een ster- of een driehoekschakeling zoeken.
Volgende sterschakelingen zijn aanwezig: sterpunt = B of E.
Volgende driehoekschakelingen zijn aanwezig: DBE en BCE.
Vervang nooit 2 schakelingen in 1 keer daar je anders het risico
KHBO
4.16
Elektriciteit
loopt een weerstand dubbel te vervangen (1x in elke schakeling).
We kiezen bvb. Om de driehoek BCE te vervangen.
Schrap de 3 te vervangen weerstanden en teken de 3 nieuwe
weerstanden:
De nieuwe schakeling ziet er als volgt uit:
C
R13
R6
D
Door de transformatie ontstaan er nieuwe serie- en/of
parallelschakelingen.
Gebeurt dat niet, dan moet je kijken als het vervangen van een
andere schakeling geen betere keuze is. Ga zelf na als er nog
mogelijkheden zijn die leiden tot nieuwe serie- en/of
parallelschakelingen.
R13 en β evenals R6 en α staan in serie.
KHBO
4.17
Elektriciteit
R6a en R13b staan nu in parallel.
Rp staat in serie met γ.
5.
Oefeningen - toepassingen
5.1.
Oefening 1
Breid het meetbereik van een ampèremeter uit van 1mA naar 5mA, als je weet dat
zijn inwendige weerstand 2k is.
5.2.
Oefening 2
Breid het meetbereik van een voltmeter uit van 1V naar 3V, als je weet dat zijn
inwendige weerstand 10k is.
5.3.
Oefening 3
Zoek R in volgende schakeling.
KHBO
4.18
Elektriciteit
5.4.
Oefening 4
Wanneer een ampèremeter parallel geplaatst wordt met een
kleine weerstand (Rs), dan beginnen de overgangsweerstanden
invloed te krijgen. Op onderstaand schakeling staan die
overgangsweerstanden aangeduid (a, b, c).
Rm
a
It
Ia
a
A
c
c
b
b
Is
Rs
Deze praktische schakeling kan omgevormd worden tot volgend
elektrisch schema:
Ia
c
c
b
a
It
Rm
Is
b
Rs
a
De weerstanden a,b,c staan in driehoek geschakeld. Deze
driehoek kan omgevormd worden tot een ster:
Ia
It
Rm



X
Y

Is
KHBO
Rs


4.19
Elektriciteit
Er ontstaan serieschakelingen die als volgt kunnen
vereenvoudigd worden:
Ia
It
2+Rm

X
Y
Is

2+Rs
De stroomverdeling tussen de tak met de ampèremeter en de tak
met de kleine weerstand Rs wordt beïnvloed door de
weerstanden en . Dat betekent dat het meetbereik van de
nieuwe schakeling wordt beïnvloed door deze weerstanden en
.
Bepaal het meetbereik dat bekomen wordt als je parallel met een
ampèremeter (met meetbereik van 1mA en Rm= 1k) een
weerstand Rs=0,1plaatst.
a) Als je de overgangsweerstanden (a,b,c) verwaarloost.
Tip: zie 5.1 oefening 1. (10,001A=10A)
b) Als je de overgangsweerstanden (a=b=c=0,05) niet
verwaarloost.
Tip: na het berekenen van  eb  bereken je eerst de spanning
tussen X en Y. (7,50125A=7,5A)
Na deze berekening wordt het duidelijk dat de overgangsweerstanden een grote
invloed kunnen spelen bij kleine weerstandswaarden. Daarom worden die kleine
waarden uitgevoerd met 4 aansluitklemmen.
KHBO
4.20
Elektriciteit
Hierdoor wordt de overgangsweerstand c (tussen de 2 verbindingsdraden)
vermeden.
Het elektrisch equivalent wordt:
Ia
b
a
It
Is
X
Rm
Rs
b
a
Y
Bewijs zelf dat de overgangsweerstanden (a en b) nu zo goed als geen invloed meer
hebben op het meetbereik.
5.5.
Oefening 5
Zoek de spanning U op volgende schakeling:
KHBO
4.21
Elektriciteit
6.
Brug van Wheatsone
6.1.
Oefening:
Bepaal bij welke waarde van R4 de spanning U = 0.
KHBO
4.22
Elektriciteit
6.2.
Toepassing:
De formule die werd afgeleid in vorige oefening wordt gebruikt
om zeer nauwkeurig weerstanden te bepalen.
Op de plaats van R4 wordt een onbekende weerstand geplaatst.
R3 wordt vervangen door een instelbare weerstand waarvan de
ingestelde waarde kan afgelezen worden. R1 en R2 zijn gekende
waarden.
R3 wordt gewijzigd tot er geen spanning meer is tussen B en C.
Op dat ogenblik geldt dat :
R1 * R 4  R 2 * R3  R 4 
R 2 * R3
R1
Merk op: als er geen spanning is tussen A en B, dan vloeit er ook
geen stroom in de weerstand van 1k. Meestal plaatst men een
zeer gevoelige ampèremeter (nA) tussen A en B. s
KHBO
4.23
Elektriciteit
Hoofdstuk4Hetschakelenvanweerstanden.
1.
2.
Doel. .................................................................................... 4.1
Theoretische achtergrond voor het schakelen van weerstanden. .... 4.1
2.1. Serieschakeling.................................................................. 4.1
2.1.1. Merk op: ...................................................................... 4.1
2.2. Parallelschakeling............................................................... 4.2
2.2.1. Merk op: ...................................................................... 4.2
2.3. Ster- driehoek transformatie................................................ 4.4
2.3.1. Van driehoek naar ster. ................................................. 4.4
2.3.2. Van ster naar driehoek. ................................................. 4.7
3. Werkwijze. ............................................................................ 4.8
3.1. Nummeren van de knopen. ................................................. 4.8
3.2. Vereenvoudigen van de schakeling. ...................................... 4.9
3.2.1. Serieschakelingen ........................................................4.10
3.2.2. Parallelschakelingen. ....................................................4.11
3.2.3. Ster- driehoek transformatie..........................................4.12
4. Voorbeelden: ........................................................................4.13
4.1. Welke stappen moet je uitvoeren om de weerstand tussen A en B
te bepalen? .............................................................................4.13
4.1.1. Oplossing: ..................................................................4.13
4.2. Welke stappen moet je uitvoeren om de weerstand tussen A en B
te bepalen? .............................................................................4.14
4.2.1. Oplossing: ..................................................................4.14
4.3. Welke stappen moet je uitvoeren om de weerstand tussen A en B
te bepalen? .............................................................................4.15
4.3.1. Oplossing: ..................................................................4.15
4.4. Welke stappen moet je uitvoeren om de weerstand tussen C en D
te bepalen? .............................................................................4.16
4.4.1. Oplossing: ..................................................................4.16
5. Oefeningen - toepassingen......................................................4.18
5.1. Oefening 1 .......................................................................4.18
5.2. Oefening 2 .......................................................................4.18
5.3. Oefening 3 .......................................................................4.18
5.4. Oefening 4 .......................................................................4.19
5.5. Oefening 5 .......................................................................4.21
6. Brug van Wheatsone ..............................................................4.22
6.1. Oefening: ........................................................................4.22
6.2. Toepassing: .....................................................................4.23
KHBO
4.24