Toets elektriciteit

Toets elektriciteit
Dinsdag 4 november 2003
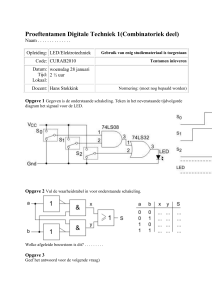
Opgave 1: (9 punten) Gegeven is de onderstaande schakeling:
500 
200 
R = 100 
100 
a
b
Iab
400 
300 
-
+
100 V
Voer de eerste stap uit van de stelling van Norton. Anders gezegd, bereken IN = Iabk.
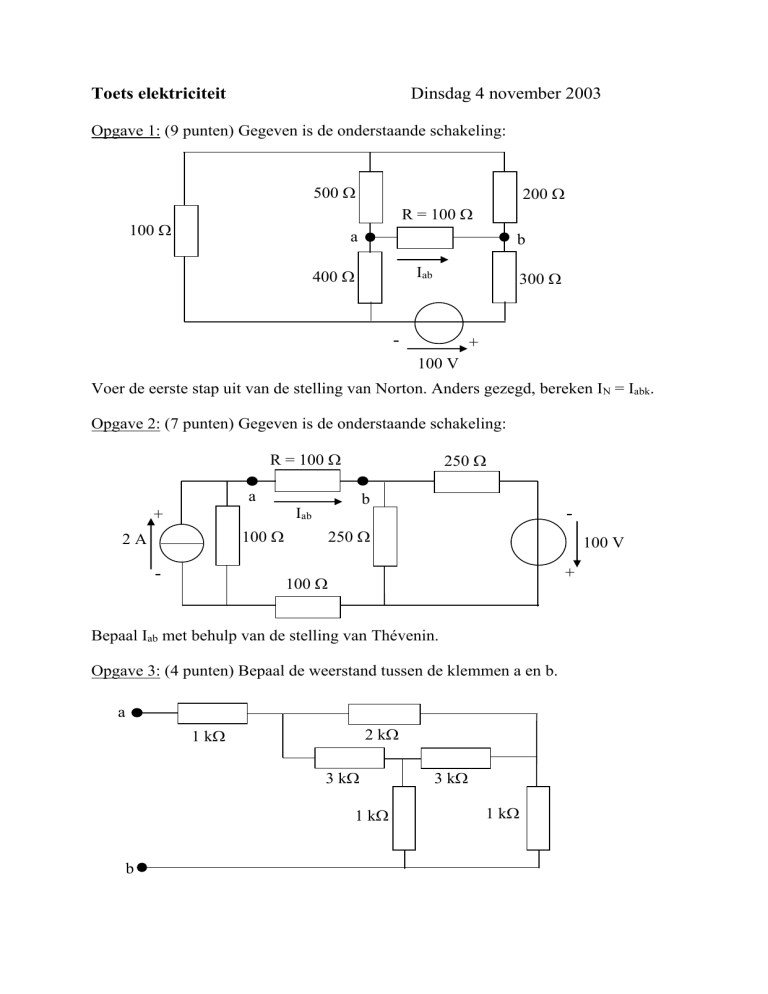
Opgave 2: (7 punten) Gegeven is de onderstaande schakeling:
R = 100 
250 
a
b
-
Iab
+
250 
100 
2A
-
100 V
+
100 
Bepaal Iab met behulp van de stelling van Thévenin.
Opgave 3: (4 punten) Bepaal de weerstand tussen de klemmen a en b.
a
2 k
1 k
3 k
1 k
b
3 k
1 k
Oplossing Opgave 1:
We geven hier twee oplossingsmethodes. De eerste oplossingmethode heeft geen
behoefte aan een driehoek-ster-transformatie, de tweede oplossingsmethode heeft daar
wel behoefte aan. De tweede oplossingsmethode is korter en eenvoudiger.
Eerste oplossingsmethode:
De weerstand R = 100  wordt vervangen door een kortsluiting. We zoeken Iabk.
Bemerk de extra aangeduide stromen I1, I2, I4 en I5.
500 
200 
I5
100 
I4
a
b
Iabk
400 
I1
I2
-
300 
+
100 V
De bovenstaande schakeling kan hertekend worden tot de onderstaande figuur. Hierbij
verdwijnt Iabk, maar I1, I2, I3, I4, I5 kunnen vlot berekend worden.
500 
200 
I5
I4
I3
100 
400 
I1
I2
-
300 
+
100 V
Bemerk dat de weerstand van 500  parallel staat met de weerstand van 200  en dat
deze parallelschakeling in serie staat met de weerstand van 100 . Reken zelf na dat I1
= 221,6 mA.
Door de spanningswet van Kirchoff toe te passen weet u dat
100V – I1 300 - I2 400 = 0 zodat I2 = 83,8 mA.
Hieruit volgt dat I3 = 137,8 mA en dat I5 = 39,4 mA.
Deze berekende stromen I1, I2, I3, I5 kunt u aanduiden op de originele figuur waar Iabk
wel op aanwezig is. Steunende op de stroomwet van Kirchoff in het punt a volgt dat
Iabk = - I2 - I5 = -123,2 mA.
Tweede oplossingsmethode:
De weerstand R = 100  wordt vervangen door een kortsluiting. We zoeken Iabk.
500 
100 
200 
a
b
Iabk
400 
300 
-
+
100 V
Bemerk de aanwezigheid van een driehoek bestaande uit de weerstanden van 100 ,
400  en 500 . Door hierop een driehoek-ster-transformatie uit te voeren, bekomt
men het onderstaande schema.
50 
200 
a
b
200 
Iabk
300 
40 
-
+
100 V
I
De 100 V spanningsbron levert een stroom I van 0,222 A. Dit geeft aanleiding tot een
Iabk = -0,123 A. Let hierbij op het teken van de stroom.
Oplossing Opgave 2:
Stap 1: Bepalen Uabo
250 
Uabo
a
b
-
+
200 V
2A
-
100 
250 
50 V
100 V
+
100 
Op de bovenstaande figuur is de weerstand R weggenomen. Teneinde Uabo te vinden,
verifieert u eerst dat er 200 V staat over de linkerweerstand van 100  en dat er 50 V
staat over de linkerweerstand van 250 . Via de spanningswet van Kirchoff in de
middelste kring is het duidelijk dat Uabo = 250 V (bemerk dat er geen spanning staat
over de onderste weerstand van 100 ).
250 
Stap 2: Bepalen RV
a
b
100 
250 
100 
Bij het bepalen van RV gezien vanuit de klemmen a en b, wordt de rechter
spanningsbron kortgesloten en wordt de linker stroombron een open keten. De
schakeling herleidt zich tot een eenvoudige serie-parallelschakeling zodat RV = 325 .
Stap 3: Berekenen Iab
Hier is Iab = Uabo/(RV + R) = 588 mA. Teken ook het Thévenin equivalent schema.
Oplossing Opgave 3:
Bij het bepalen van de weerstand Rab tussen de klemmen a en b is het belangrijk de
driehoek bestaande uit 2 keer 3 k en 1 keer 2 k te herkennen. Voer vanuit deze
driehoek een driehoek-ster-transformatie uit. Zo krijgt u het onderstaande netwerk:
1 k
0,75 k
0,75 k
a
1,125 k
1 k
1 k
b
Reken na dat Rab = 2,7 k.