Dia 1 - R. van Moppes

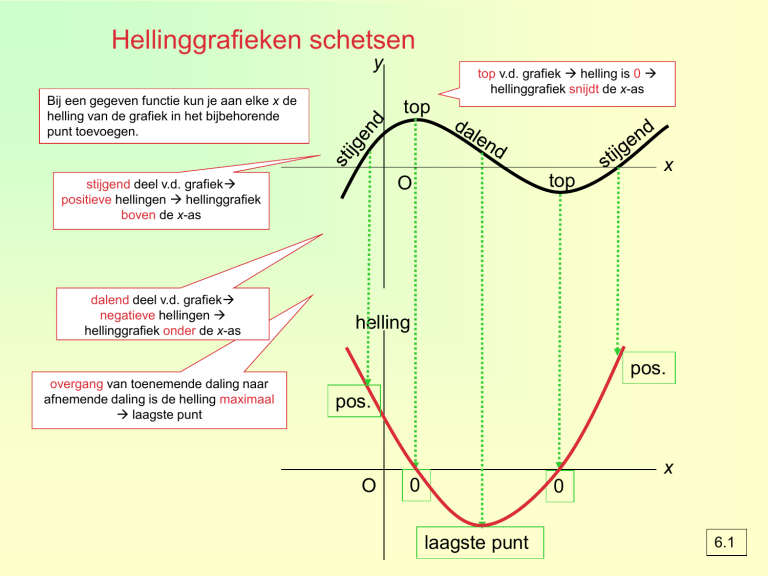
Hellinggrafieken schetsen
y
Bij een gegeven functie kun je aan elke x de
helling van de grafiek in het bijbehorende
punt toevoegen.
top
top
O
stijgend deel v.d. grafiek
positieve hellingen  hellinggrafiek
boven de x-as
dalend deel v.d. grafiek
negatieve hellingen 
hellinggrafiek onder de x-as
top v.d. grafiek  helling is 0 
hellinggrafiek snijdt de x-as
x
helling
pos.
overgang van toenemende daling naar
afnemende daling is de helling maximaal
 laagste punt
pos.
x
O
0
0
laagste punt
6.1
opgave 4
a
b
c
d
e
x < -3 hellinggrafiek onder de x-as
de grafiek is dalend op ⟨  , -3 ⟩
f heeft een top bij x = -3 omdat de
hellinggrafiek daar de x-as snijdt
dat is het laagste punt
f is stijgend op ⟨ -3 , 0 ⟩
hoogste punt
schets
y
top
top
x
O
top
top
6.1
Hellinggrafiek plotten
m.b.v. GR
TI  MATH – MATH - menu
optie nDeriv
Casio  OPTN – CALC – menu
optie d/dx
vb. voer in y1 = 0,1x4 – x2 + x + 8
en y2 = nDeriv(y1,x,x) (op de TI)
of y2 = d/dx(y1,x)
(op de Casio)
6.1
top
y
top
opgave 7
a
b
voer in y1 = -0,1x³ + x² - 2x + 5
en y2 = nDeriv(y1,x,x) (op de TI)
of y2 = d/dx(y1,x)
(op de Casio)
kies Xmin = -2 , Xmax = 10 ,
Ymin = -10 , Ymax = 10
helling =
[]
dy
dx
= y2(7) = -2,7
x=7
x
O
helling
top
x
O 0
0
y
opgave 9
O
a
b
voer in y1 = (5x² - 38)/(x² + 4)
en y2 = nDeriv(y1,x,x) (op de TI)
of y2 = d/dx(y1,x)
(op de Casio)
kies Xmin = -5 , Xmax = 5 ,
Ymin = -10 , Ymax = 5
voer in y3 = 3
optie intersect met y2 en y3 geeft
x ≈ 0,458 en x ≈ 2,354
aflezen  helling > 3
voor 0,458 < x < 2,354
x
helling
3
O 0,458
2,354
x
De afgeleide functie
Bij een functie hoort een hellingfunctie.
i.p.v. hellingfunctie wordt meestal de naam afgeleide functie of afgeleide gebruikt
notatie : f’ (f-accent)
De afgeleide van een functie f geeft voor elke x :
- de richtingscoëfficiënt van de raaklijn van f in het bijbehorende punt
- de helling van de grafiek van f in het bijbehorende punt
3.4
Om de formule van de afgeleide van een functie f te vinden, kijken we naar het
differentiecoëfficiënt van f(x) op het interval [ x, x + h ] , dus naar
f(x + h) – f(x)
f(x + h) – f(x)
∆y
=
=
h
∆x
x+h-x
Neem je op het interval [ x,x + h ] de waarde van h heel klein, dan geeft
f(x + h) – f(x)
een goede benadering van de r.c. van de raaklijn van de grafiek van f
h
in het bijbehorende punt.
y
f(x+h)
y
f(x+h) – f(x)
f(x)
O
h klein
h
x
f(x+h)
f(x)
f(x+h) – f(x)
h
x+h x
O
x x+h
f(x + h) – f(x)
voor h naar 0 is de afgeleide f’(x)
h
de definitie van de afgeleide f’ van een functie f is
f(x + h) – f(x)
f’(x) = lim
h
h0
x
de grenswaarde van
3.4
Voorbeeld limietstelling. Neem de functie :
f ( x)  2 x 2  4 x  12
y lim
f ( x  h)  f ( x )

x h  0
h
y lim
(2( x  h) 2  4( x  h)  12)  (2 x 2  4 x  12)

x h  0
h
y lim
2( x 2  2hx  h 2 )  4 x  4h  12  2 x 2  4 x  12

x h  0
h
y lim
2 x 2  4hx  2h 2  4 x  4h  12  2 x 2  4 x  12

x h  0
h
y lim
4hx  2h 2  4h

x h  0
h
y lim
 4 x  2h  4
x h  0
y
 4x  4
x
De afgeleide functie
Bij een functie hoort een hellingfunctie.
i.p.v. hellingfunctie wordt meestal de naam
afgeleide functie of afgeleide gebruikt.
notatie : f’ (f-accent)
regels voor de afgeleide :
f(x) = a geeft f’(x) = 0
f(x) = ax geeft f’(x) = a
f(x) = ax² geeft f’(x) = 2ax
6.2
opgave 14a
f(x) = (2x – 7)(8 + x)
f(x) = 16x + 2x² - 56 – 7x
f(x) = 2x² + 9x – 56
f’(x) = 2 · 2x + 9
f’(x) = 4x + 9
eerst haakjes
wegwerken
dezelfde termen
optellen
somregel van
differentiëren
6.2
opgave 15c
h(x) = 5(x – 3)² + 5(x – 1) + 8
h(x) = 5(x – 3)(x – 3) + 5x – 5 + 8
h(x) = 5(x² - 6x + 9) + 5x + 3
h(x) = 5x² - 30x + 45 + 5x + 3
h(x) = 5x² - 25x + 48
h’(x) = 2 · 5x – 25
h’(x) = 10x - 25
opgave 15d
k(x) = -3(x – 1)(5 – 2x) – 8(x – 7)
k(x) = -3(5x – 2x² - 5 + 2x) – 8x + 56
k(x) = -15x + 6x² + 15 – 6x – 8x + 56
k(x) = 6x² - 29x + 71
k’(x) = 2 · 6x – 29
k’(x) = 12x - 29
De afgeleide van f(x) = axn
f(x) = ax3
f’(x) = 3ax²
g(x) = ax4
g’(x) = 4ax3
h(x) = ax5
h’(x) = 5ax4
algemeen geldt:
k(x) = axn
k’(x) = n · axn-1
oude exponent
ervoor zetten
nieuwe exponent 1
minder (4 – 1 = 3)
opgave 17a
f(x) = 5x4 – 3x3 + 2x
f’(x) = 4 · 5x3 – 3 · 3x2 + 2
f’(x) = 20x3 – 9x2 + 2
opgave 18b
g(x) = 7(3x – 2)(x² + 2x)
g(x) = 7(3x3 + 6x2 - 2x2 – 4x)
g(x) = 21x3 + 42x2 – 14x2 – 28x
g(x) = 21x3 + 28x2 – 28x
g’(x) = 3 · 21x2 + 2 · 28x – 28
g’(x) = 63x2 + 56x - 28
opgave 18d
h(x) = 3px8 – px4
h’(x) = 8 · 3px7 – 4 · px3
h’(x) = 24px7 – 4px3
Vergelijking van raaklijn met behulp van de afgeleide
Je weet dat de afgeleide f’ aan elke x de
helling in het bijbehorende punt van de
grafiek van f toevoegt
of
f’(x) is de rc van de raaklijn in het
bijbehorende punt.
y
f
k
algemeen:
f’(a) is de rc van de raaklijn van de grafiek
van f in het punt A(a, f(a))
A
x
O
xA
yA = f(xA)
rck = f’(xA)
6.3
opgave 20
a
f(x) = 0,5x3 – 2x2 + 2
f’(x) = 3 · 0,5x2 – 2 · 2x
f’(x) = 1,5x2 – 4x
stel k : y = ax + b
xA = 4
a = f’(4) = 1,5 · 42 – 4 · 4 = 8
dit geeft k : y = 8x + b
y = f(4) = 0,5 · 43 – 2 · 42 + 2 = 2
2=8·4+b
2 = 32 + b
b = -30
dus k : y = 8x - 30
6.3
opgave 20
b
stel m : y = ax + b
xB = -1
a = f’(-1) = 1,5 · (-1)2 – 4 · -1 = 5,5
dit geeft m : y = 5,5x + b
y = f(-1) = 0,5 · (-1)3 – 2 · (-1)2 + 2 = -0,5
dus m : y = 5,5x + 5
-0,5 = 8 · -1 + b
-0,5 = -5,5 + b
b=5
opgave 23
a
h(x) = (x – 1)(x – 4)
h(x) = x2 – 4x – 1x + 4
h(x) = x2 – 5x + 4
h’(x) = 2x - 5
stel k : y = ax + b
xA = 6
a = h’(6) = 2 · 6 - 5 = 7
dit geeft k : y = 7x + b
y = h(6) = 5 · 2 = 10
dus k : y = 7x - 32
10 = 7 . 6 + b
10 = 42 + b
b = -32
opgave 23
b
stel m : y = ax + b
de grafiek h snijdt de y-as in punt B  xB = 0
a = h’(0) = 2 · 0 - 5 = -5
dit geeft m : y = -5x + b
y = f(0) = 4
B(0, 4)
dus m : y = -5x + 4
opgave 23
c
de grafiek h snijdt de x-as  y = 0
h(x) = 0  (x – 1)(x – 4) = 0
x=1 ⋁ x=4
stel de raaklijn in (1, 0) is m : y = ax + b
a = h’(1) = 2 · 1 – 5 = -3
dit geeft n : y = -3x + b
0 = -3 · 1 + b
(1, 0)
b=3
dus n : y = -3x + 3
stel de raaklijn in (4, 0) is p : y = ax + b
a = h’(4) = 2 · 4 – 5 = 3
dit geeft p : y = 3x + b
0=3·4+b
(4, 0)
b = -12
dus p : y = 3x - 12
Raaklijn met gegeven richtingscoëfficient
Teken f(x) = x² - 3x + 1
Teken enkele lijnen met rc = 2
Eén van de lijnen raakt de grafiek
het raakpunt is B.
Bereken de coördinaten van B
rc = 2 dus f’(xB) = 2
xB berekenen
f’(x) = 2 oplossen
f’(x) = 2x – 3
2x – 3 = 2
f’(x) = 2
2x = 5
x = 2,5
xB = 2,5
yB = f(2,5) = -0,25
-1
B(2,5; -0,25)
y
4
3
2
1
0
1
2
● 3
B
x
4
-1
6.3
opgave 25
f(x) = -x² + 2x + 3
a
rcraaklijn = 4
dus f’(x) = 4
f’(x) = -2x + 2
b
xA = -1
yA = f(-1) = 0
A(-1, 0)
k : y = -6x + 8
rcraaklijn = -6
dus f’(xB) = -6
f’(x) = -2x + 2
xB = 4
yB = f(4) = -5
B(4, -5)
y
4
-2x + 2 = 4
-2x = 2
x = -1
3
2
f
1
-2x + 2 = -6
A●
-2x = -8
x=4
-1
0
-1
1
2
3
4
x
k
6.3
opgave 27
a
b
f(x) = -x³ + x² + 1
f’(x) = -x² + 2x
stel l : y = ax + b
xA = 3
a = f’(3) = -3² + 2 · 3 = -3
l : y = -3x + b
1 = -3 . 3 + b
f(3) = 1
1 = -9 + b
b = 10
dus l : y = -3x + 10
rcm = rcl = -3  f’(x) = -3
-x² + 2x = -3
x² - 2x – 3 = 0
(x + 1)(x – 3) = 0
x = -1 v x = 3
xB = -1
yB = 2
m : y = -3x + b
B(-1, 2 )
dus m : y = -3x - 
2 = -3 · -1 + b
2 = 3 + b
b = -
Extreme waarden berekenen met behulp van de afgeleide
werkschema: het algebraïsch berekenen van extreme waarden
raaklijn in een top is horizontaal 
1 Bereken f’(x)
afgeleide is 0
2 Los algebraïsch op f’(x) = 0
3 Voer de formule van f in op de GR.
Plot en schets de grafiek.
Kijk in de grafiek of je met max. en/of min. te maken hebt.
4 Bereken de y-coördinaten van de toppen en
noteer het antwoord in de vorm max. is f(…) = …
en min. is f(…) = …
6.3
opgave 30a
f(x) = x³ + 3½x² + 10x + 5
f’(x) = x² + 7x + 10
f’(x) = 0 geeft
x² + 7x + 10 = 0
(x + 2)(x + 5) = 0
x = -2 ⋁ x = -5
voer f in op je GR
optie maximum
max. is f(-5) =  en
optie minimum
min. is f(-2) = -3
y
●
x
-5
-2
●
O
50
opgave 32
a
b
f(x) = -x³ - 3x² + 24x + 10
f’(x) = -3x² - 6x + 24
f’(x) = 0 geeft
-3x² - 6x + 24 = 0
x² + 2x – 8 = 0
(x + 4)(x – 2) = 0
x = -4 ⋁ x = 2
voer f in op je GR
optie minimum
min. is f(-4) = -70
optie maximum
max. is f(2) = 38
f(x) = -50  3 oplossingen
y = -50  snijdt de grafiek van f 3 keer
f(x) = 50  1 oplossing
y = 50  snijdt de grafiek van f 1 keer
38
y
●
x
-4
O
2
-50
●
-70
c
d
f(x) = p  3 oplossingen
-70 < p < 38
f(x) = p  1 oplossing
p < -70 ⋁ p > 38
In de praktijk gaat het bij problemen vaak om het
vinden van een maximum of minimum
Voorbeelden van optimaliseringsproblemen zijn:
• Bij welke afmetingen is de oppervlakte bij een gegeven omtrek het grootst ?
• Wat zijn de afmetingen van de doos met de grootste inhoud die je uit een gegeven
rechthoekig stuk karton kunt maken ?
• Bij welke route horen de laagste kosten ?
6.4
opgave 35
a
b
stel AD = x
CD + 2x = 40
CD = 40 – 2x
O = AD · CD
O = x(40 – 2x)
O = 40x – 2x²
dO
= 40 – 4x
dx
dO
=0
dx
O
200
40 – 4x = 0
-4x = -40
x = 10
AD = 10 m.
CD = 40 – 20 = 20 m.
x
O
10
6.4
Extra opgave
De totale lengte van het hekwerk is
160 meter.
Druk de oppervlakte van het
perceel uit in x?
Voor welke x is de oppervlakte van
het grasland maximaal?
opgave 42
a
b
c
4 · lengte + 4 · hoogte + 4 · breedte = 12
:4
lengte + hoogte + breedte = 3
4x + h + x = 3
5x + h = 3
l
h = 3 – 5x
I=l·b·h
0,64
I = 4x · x · (3 – 5x)
I = 4x²(3 – 5x)
I = 12x² - 20x³
dl
dl
=
24x
–
60x²
dx = 0
dx
24x – 60x² = 0
12x(2 – 5x) = 0
12x = 0 ⋁ 2 – 5x = 0
O
0,4
x = 0 ⋁ -5x = -2
x = 0 ⋁ x = 0,4
x = 0,4  lmax = 0,64 m³
bij x = 0,4 hoort
h = 3 – 5 · 0,4
h = 1 m.
x
opgave 44
y = 9 - x²
op de parabool ligt punt P met xP = p
PQ = yP
PQ = 9 - p²
O(∆OPQ) = ½ · OQ · PQ
O(∆OPQ) = ½p · (9 - p²)
O(∆OPQ) = 4,5p – 0,5p³
dO = 4,5 – 1,5p²
yP
O
3√3
dp
dO
dp = 0
4,5 – 1,5p² = 0
-1,5p² = -4,5
p² = 3
p = √3 ⋁ p = -√3
O
√3
Omax = 4,5 · √3 – 0,5 · (√3)³
Omax = 4,5√3 – 0,5 · 3√3
Omax = 4,5√3 – 1,5√3 = 3√3
p
opgave 45
f(x) = 1 - x²
g(x) = 1 - x³
verticale lijn : x = p
O = O(∆OPR) – O(∆OPQ)
O = O(∆OQR)
O = ½ · OP · QR
O = ½ · p · ((1 - p³) – (1 - p²))
O = ½p(p²- p³)
O = ½p³ - ½p4
dO
= 1½p² - 2p³
O
0,05
dp
dO
dp = 0
1½p² - 2p³ = 0
p²(1½ - 2p) = 0
p = 0 ⋁ 1½ - 2p = 0
O
¾
1
p = 0 ⋁ 2p = 1½
p=0 ⋁ p=¾
O is maximaal voor p = ¾
p