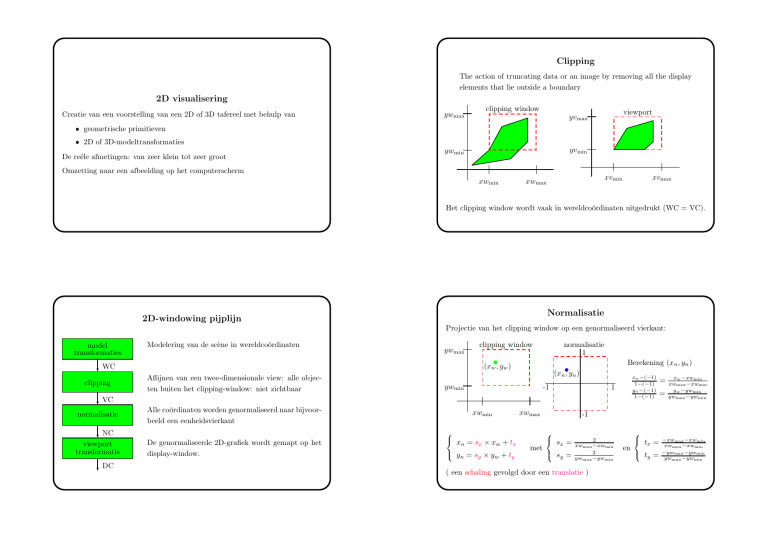
Clipping
The action of truncating data or an image by removing all the display
elements that lie outside a boundary
2D visualisering
Creatie van een voorstelling van een 2D of 3D tafereel met behulp van
ywmax
clipping window
viewport
yvmax
• geometrische primitieven
• 2D of 3D-modeltransformaties
De reële afmetingen: van zeer klein tot zeer groot
yvmin
ywmin
Omzetting naar een afbeelding op het computerscherm
xwmin
xvmin
xwmax
xvmax
Het clipping window wordt vaak in wereldcoördinaten uitgedrukt (WC = VC).
Normalisatie
2D-windowing pijplijn
Projectie van het clipping window op een genormaliseerd vierkant:
model
transformaties
Modelering van de scène in wereldcoördinaten
ywmax
normalisatie
1
Berekening (xn , yn )
(xw , yw )
WC
clipping
clipping window
Aflijnen van een twee-dimensionale view: alle objecten buiten het clipping-window: niet zichtbaar
(xn , yn )
ywmin
-1
1
VC
normalisatie
NC
viewport
transformatie
DC
Alle coördinaten worden genormaliseerd naar bijvoorbeeld een eenheidsvierkant
De genormaliseerde 2D-grafiek wordt gemapt op het
display-window.
xwmin
x =s ×x +t
x
w
x
n
yn = sy × yw + ty
xwmax
s =
x
met
sy =
xn −(−1)
1−(−1)
yn −(−1)
1−(−1)
=
=
xw −xwmin
xwmax −xwmin
yw −ywmin
ywmax −ywmin
-1
2
xwmax −xwmin
2
ywmax −ywmin
( een schaling gevolgd door een translatie )
t =
x
en
ty =
−xwmax −xwmin
xwmax −xwmin
−ywmax −ywmin
ywmax −ywmin
Viewport
Homogene coördinaten
Van de genormaliseerde scène naar het actieve window op het scherm:
Stelling:
normalisatie
1
viewport
yvmax
Berekening (xv , yv )
(xv , yv )
(xn , yn )
-1
1
xvmin
-1
x = s′ × x + t′
n
v
x
x
yv = s′ × yn + t′
y
xv −xvmin
xvmax −xvmin
yv −yvmin
yvmax −yvmin
yvmin
y
s′ =
x
met
s′ =
y
=
=
xn −(−1)
1−(−1)
yn −(−1)
1−(−1)
xvmax
xvmax −xvmin
2
yvmax −yvmin
2
( een schaling gevolgd door een translatie )
een probleem in een n-dimensionale ruimte heeft telkens een overeenkomstig probleem in een (n + 1) dimensionale ruimte
Vaststelling:
de oplossing van een probleem in de ruimte met dimensie (n + 1)
is vaak eenvoudiger te bekomen dank zij de extra vrijheidsgraad
De oplossing in de (n + 1)-dimensionale ruimte kan dan op de één of andere
manier geprojecteerd worden naar de ruimte met dimensie n.
Homogeniseren van een punt met twee coördinaten (x, y): toevoegen van een
derde coördinaat w 6= 0, de schaalfactor.
t′ =
x
en
t′ =
y
xvmax +xvmin
2
yvmax +yvmin
2
Het punt wordt nu bepaald door drie coördinaten: (wx, wy, w).
Projectie van een punt (16, 8, 4): (16/4, 8/4) of (4, 2).
3D: punt (x, y, z) homogeniseren: schaalfactor toevoegen (x, y, z, 1)
Coördinaten transformaties mbv. homogene coördinaten
Matrix notatie
• wereldcoördinaten naar genormaliseerde coördinaten
#
# "
#"
# "
"
tx
xw
sx 0
xn
+
=
ty
yw
0 sy
yn
• genormaliseerde coördinaten naar schermcoördinaten
"
# "
#"
#
# "
xv
s′x 0
xn
t′x
=
+
yv
0 s′y
yn
t′y
zowel een matrix vermenigvuldiging als een optelling:
kan niet efficiënt door de grafische processor berekend worden
Punt: een 3 × 1 kolommatrix
transformatiematrix: een 3 × 3 matrix
• wereldcoördinaten naar genormaliseerde coördinaten
i
i h
ih
i h
h
xn
yn
=
0
sx
0
xw
yw
sy
sx
0
yn = 0
0
1
sy
xn
0
tx
+
tx
ty
xw
ty
yw
1
1
• genormaliseerde coördinaten naar schermcoördinaten
xn
xv
s′
0 t′x
x
yv = 0 s′ t′ yn
y
y
1
0 0 1
1
window-to-viewport transformatie
Schermcoördinaten ← genormaliseerde coördinaten ← wereld coördinaten
xvmax −xvmin
min
xv
0 xvmax +xv
2
2
yvmax +yvmin
yv =
min
0 yvmax −yv
2
2
1
0
0
1
xwmax +xwmin
2
xw
0 − xw
xwmax −xwmin
max −xwmin
ywmax +ywmin
2
×
×
− yw
0 ywmax −yw
yw
min
max −ywmin
1
0
0
1
xv
yv =
1
xvmax −xvmin
xwmax −xwmin
0
0
yvmax −yvmin
ywmax −ywmin
0
0
xwmax xvmin −xwmin xvmax
xwmax −xwmin
ywmax yvmin −ywmin yvmax
ywmax −ywmin
xw
yw
1
1
2D viewing transformatie in OpenGL
1. selecteren van de juiste matrixmode: glMatrixMode(GL PROJECTION);
de top-of-stack van de projectiematrix-stack wordt de actieve matrix
de default-waarde is de eenheidsmatrix;
na wijzigen van de projectparameters kan terug de eenheidsmatrix
geladen worden:
glLoadIdentity();
2. definitie van een tweedimensionaal clipping window:
gluOrtho2D( GLdouble l e f t , GLdouble r i g h t ,
GLdouble bottom , GLdouble top ) ;
left (xwmin ), right (xwmax ), bottom (ywmin ), top (ywmax )
3. bepalen van transformatie van genormaliseerde naar schermcoördinaten:
g l V i e w p o r t ( GLint x , GLint y , GLint b reed , GLint hoog ) ;
x (xvmin ), y (yvmin ), breed (xvmax − xvmin ), hoog (yvmax − yvmin )
Voorbeeld
glViewport (0 , 0 , 600 , 4 0 0 ) ;
gluOrtho2D( −2.5 , 2 . 5 , −1.0 , 3 . 0 ) ;
120
0
0
0
300
100 100
0
1
420.0
←
200.0
1.0
300
←
0
0
0
300
200 200
0
1
0.4
0.0
1.0
0.4
0
0
←
0
0
0.5 −0.5
0
1
1.0
1.0
1.0












