Snel Grootste Gemene Delers uitrekenen

Snel Grootste Gemene Delers uitrekenen
Technische Universiteit Eindhoven: Bachelorproject
Bouke Cloostermans 0640381
19 juni 2012
Tijdens mijn bachelorproject heb ik mij bezig
gehouden met het uitrekenen van Grootste Gemene Delers (GGD’s). De GGD van twee getallen
is het grootste getal dat beide getallen deelt.
Bijvoorbeeld, de GGD van 12 en 8 is 4.
Het uitrekenen van een GGD is niet heel moeilijk.
Er zijn documenten uit het jaar 300 B.C. waarin
al het algoritme van Euclides staat om de GGD
van twee getallen uit te rekenen. Een algoritme
is een stappenplan om een probleem systematisch
op te lossen. Dit algoritme wordt vandaag de dag
nog steeds gebruikt, dus waarom zou je hier nog
dingen willen verbeteren?
Het nadeel van het algoritme van Euclides is dat
het naarmate de twee getallen waarmee je begint
groter worden het heel veel langzamer wordt om de
GGD van de getallen uit te rekenen. Ik heb tijdens
mijn bachelorproject twee algoritmes bestudeerd
en hiervoor een computerprogramma gemaakt die
weliswaar voor kleine getallen langzamer zijn dan
het algoritme van Euclides maar naarmate de
getallen groter worden hebben ze weinig extra tijd
nodig. Deze algoritmes zijn dus uitermate geschikt
voor het uitrekenen van GGD’s van zeer grote
getallen.
Deze algoritmes zijn recursieve algoritmes. Dat
wil zeggen: ze herhalen zichzelf een aantal keren
met een steeds eenvoudiger wordend probleem. Zo
begin je met twee hele grote getallen waarvan je de
GGD wil weten, bijvoorbeeld getallen van 10000
cijfers. Het recursieve algoritme versimpelt deze
eerst naar 5000, dan naar 2500 enzovoorts. Zo
wordt het probleem snel veel eenvoudiger.
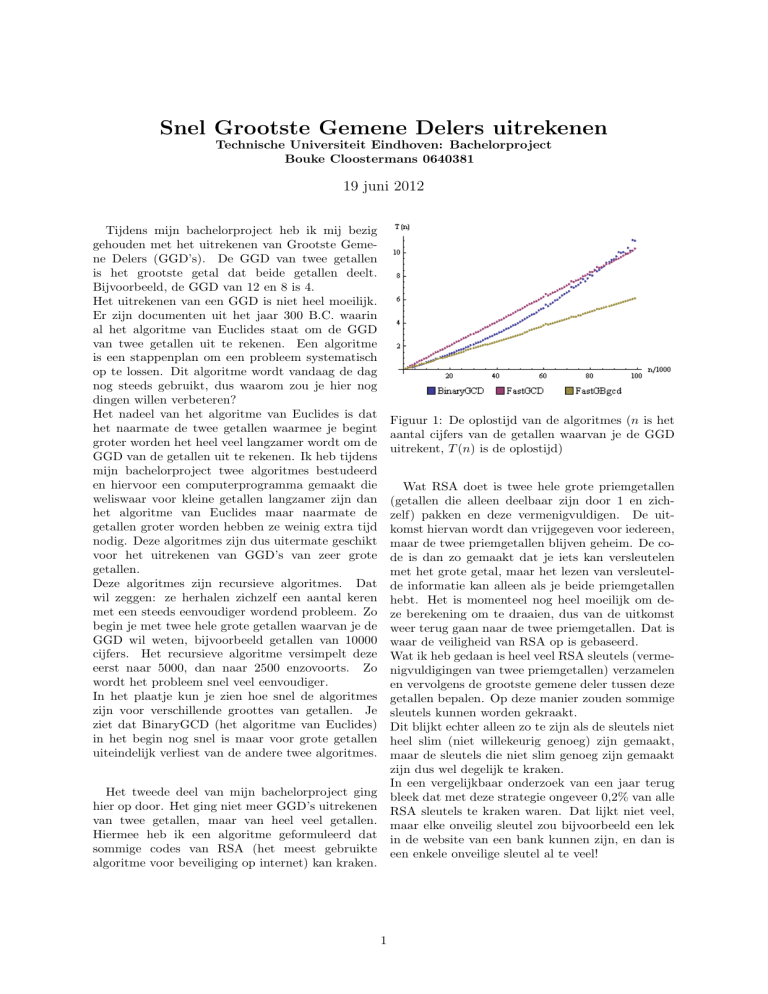
In het plaatje kun je zien hoe snel de algoritmes
zijn voor verschillende groottes van getallen. Je
ziet dat BinaryGCD (het algoritme van Euclides)
in het begin nog snel is maar voor grote getallen
uiteindelijk verliest van de andere twee algoritmes.
Figuur 1: De oplostijd van de algoritmes (n is het
aantal cijfers van de getallen waarvan je de GGD
uitrekent, T (n) is de oplostijd)
Wat RSA doet is twee hele grote priemgetallen
(getallen die alleen deelbaar zijn door 1 en zichzelf) pakken en deze vermenigvuldigen. De uitkomst hiervan wordt dan vrijgegeven voor iedereen,
maar de twee priemgetallen blijven geheim. De code is dan zo gemaakt dat je iets kan versleutelen
met het grote getal, maar het lezen van versleutelde informatie kan alleen als je beide priemgetallen
hebt. Het is momenteel nog heel moeilijk om deze berekening om te draaien, dus van de uitkomst
weer terug gaan naar de twee priemgetallen. Dat is
waar de veiligheid van RSA op is gebaseerd.
Wat ik heb gedaan is heel veel RSA sleutels (vermenigvuldigingen van twee priemgetallen) verzamelen
en vervolgens de grootste gemene deler tussen deze
getallen bepalen. Op deze manier zouden sommige
sleutels kunnen worden gekraakt.
Dit blijkt echter alleen zo te zijn als de sleutels niet
heel slim (niet willekeurig genoeg) zijn gemaakt,
maar de sleutels die niet slim genoeg zijn gemaakt
zijn dus wel degelijk te kraken.
In een vergelijkbaar onderzoek van een jaar terug
bleek dat met deze strategie ongeveer 0,2% van alle
RSA sleutels te kraken waren. Dat lijkt niet veel,
maar elke onveilig sleutel zou bijvoorbeeld een lek
in de website van een bank kunnen zijn, en dan is
een enkele onveilige sleutel al te veel!
Het tweede deel van mijn bachelorproject ging
hier op door. Het ging niet meer GGD’s uitrekenen
van twee getallen, maar van heel veel getallen.
Hiermee heb ik een algoritme geformuleerd dat
sommige codes van RSA (het meest gebruikte
algoritme voor beveiliging op internet) kan kraken.
1