hoofdstuk 3 - science.uu.nl project csg

Discussievragen met Antwoorden HOOFDSTUK 3
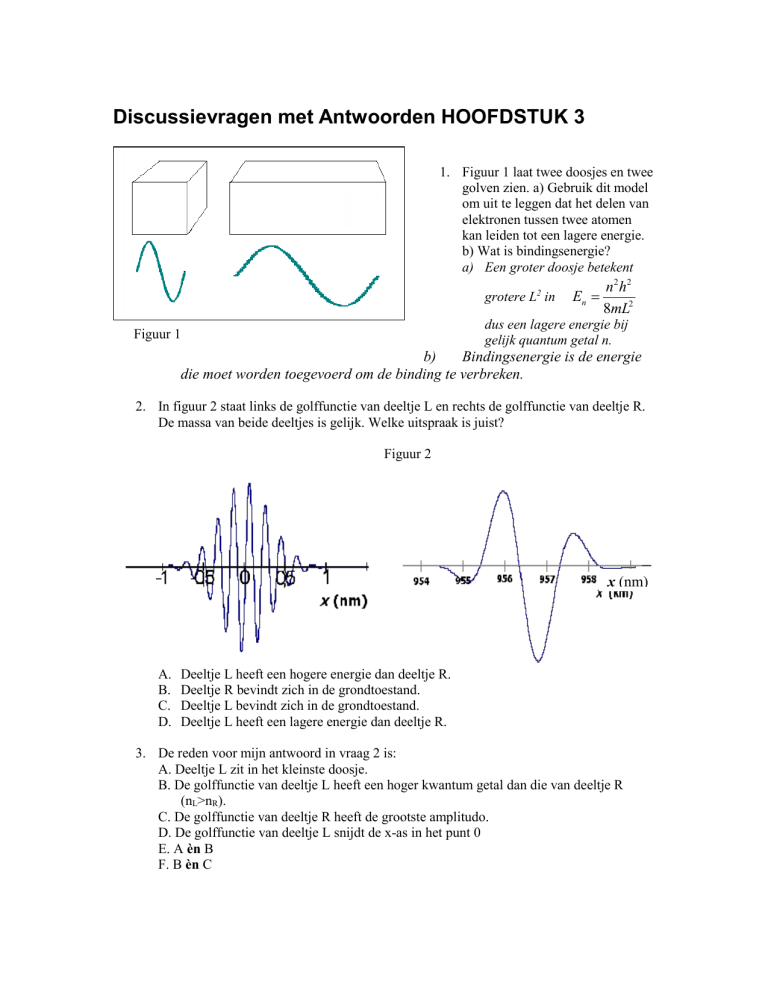
1. Figuur 1 laat twee doosjes en twee
golven zien. a) Gebruik dit model
om uit te leggen dat het delen van
elektronen tussen twee atomen
kan leiden tot een lagere energie.
b) Wat is bindingsenergie?
a) Een groter doosje betekent
2
grotere L in
n2 h2
En 
8mL2
dus een lagere energie bij
gelijk quantum getal n.
Figuur 1
b)
Bindingsenergie is de energie
die moet worden toegevoerd om de binding te verbreken.
2. In figuur 2 staat links de golffunctie van deeltje L en rechts de golffunctie van deeltje R.
De massa van beide deeltjes is gelijk. Welke uitspraak is juist?
Figuur 2
x (nm)
A.
B.
C.
D.
Deeltje L heeft een hogere energie dan deeltje R.
Deeltje R bevindt zich in de grondtoestand.
Deeltje L bevindt zich in de grondtoestand.
Deeltje L heeft een lagere energie dan deeltje R.
3. De reden voor mijn antwoord in vraag 2 is:
A. Deeltje L zit in het kleinste doosje.
B. De golffunctie van deeltje L heeft een hoger kwantum getal dan die van deeltje R
(nL>nR).
C. De golffunctie van deeltje R heeft de grootste amplitudo.
D. De golffunctie van deeltje L snijdt de x-as in het punt 0
E. A èn B
F. B èn C
Antwoord 2 en 3: Deeltje L (links) heeft een hogere energie want het zit in een kleiner doosje
(2 nm ipv 5 nm) en heeft een hoger quantum getal en dat kun je zien aan het aantal maxima
en minima van de golffunctie.
4. Elektronen die vrij komen uit een atoom bij ionisatie hebben typisch een energie van
enkele elektronvolts. Deeltjes die vrij komen uit een atoomkern zoals bij radioactieve
straling hebben een energie van enkele MeV. Verklaar. Probeer het verschil ook
kwantitatief te verklaren door de energie E1–E2 uit te rekenen in beide gevallen.
Antwoord: Verschillen in energieniveaus van elektronen in een atoom hebben typische waarden
van enkele eV. Verschillen in energieniveaus in de atoomkern zijn in de orde van enkele MeV
terwijl alfa-deeltjes die de kern uit tunnelen ook een energie van enkele MeV hebben. Kwalitatief
kunnen we dit heel goed verklaren met grote en kleine doosjes. In het kleine doosje van de kern
heeft het deeltje een kleinere golflengte en dus een hogere kinetische energie.
Kwantitatief komen we ook redelijk ver. De orde van grootte van een atoom is 10–10 m. De orde
van grootte van een kern is 10–15 m. Het energieverschil tussen het n = 1 niveau en het n = 2
niveau in een doosjesatoom wordt dan:
E2 – E1 = (h²/8me.L²).2² – (h²/8me.L²).1² = 3.h²/8.me.L² = 3.1020 .(h²/8me)
Het energieverschil tussen het n = 1 niveau en het n = 2 niveau in een doosjeskern wordt:
E2 – E1 = (h²/8mp.L²).2² – (h²/8mp.L²).1² = 3.h²/8.mp.L² = 3.1030 .(h²/8.mp) = 1,6.1027
.(h²/8.me)
waarbij in de laatste stap de massa van het proton is vervangen door de massa van het elektron.
Het verschil tussen de twee antwoorden is een factor 106. Toch aardig, nietwaar?
5. De kans een elektron in de kern van
Figuur 3
een atoom aan te treffen is heel klein.
Beredeneer dit op twee manieren: a)
m.b.v. figuur 3 (figuur 30 van p50 van
hoofdstuk 3, hiernaast
gereproduceerd) en b) door de
golflengte van een typisch atomair
elektron te vergelijken met de
afmetingen van de kern. De toelichting
op figuur 30 vermeldt dat de omvang
van de kern een factor 10–5 kleiner is
dan de breedte van de grafiek.
Antwoord: De grafiek van 2 versus x geeft voor elke locatie op de x-as de kans dat het
deeltje op die locatie gevonden kan worden. Als we een interval beschouwen, dan geeft de
oppervlakte van de grafiek van 2 op dat interval de kans dat het deeltje in dat interval
gevonden zal worden mits de grafiek genormeerd op 1, dwz dat de totale oppervlakte onder
de grafiek gelijk is aan 1 en dus de kans dat het deeltje ergens is gelijk is aan 1. De totale
breedte van deze grafiek voor een atomair elektron is ongeveer 10–10 m. De breedte van de
kern is 5x10–15 m. Als we die breedte in bovenstaande grafiek intekenen, krijgen we een lijn
die nog veel dunner is dan de y-as en dus een oppervlakte die veel kleiner is dan de
oppervlakte van de getekende as. Die oppervlakte is heel klein vergeleken bij de oppervlakte
onder de gehele grafiek.
6. Waarom kun je verwachten dat in grotere moleculen energieniveaus met kleinere verschillen
bestaan? Is dat ook zo in de natuur? Wat voor spectra kijk je naar om atomen te identificeren?
Wat voor spectra kijk je naar om grote moleculen te identificeren?
Het verschil tussen twee opeenvolgende energie niveaus is
En  En1 
(n2  (n  1) 2 )h2 (2n  1)h 2

8mL2
8mL2
Bij grotere moleculen hoort een grotere L en dus kleinere verschillen tussen energieniveaus.
De werkelijkheid is iets complexer dan ons doosjesmodel, maar grotere moleculen worden vaak
geïdentificeerd via hun vibratiespectra en die liggen in het infraroodgebied. Atomen/elementen
worden geïdentificeerd in het zichtbare en UV spectrum.
7. In een laser wordt licht weerkaatst tussen twee spiegels. Binnen metaaldraad kan een elektron
nagenoeg vrij bewegen van de ene kant van de draad naar de andere kant maar aan de
uiteinden kan het niet ontsnappen.
Geef aan om welke redenen het deeltje-in-een-doosmodel op deze beide voorbeelden van
toepassing is.
Tussen twee spiegels zijn de fotonen opgesloten als in een 1-dimensionaal doosje. Ook een
hele dunne metaaldraad kan fungeren als een 1-dimensionaal doosje voor elektronen.
8. In een massief stuk vaste stof van een kubieke meter zitten typisch in de orde van grootte van
1029 atomen.
Reken dit na voor enkele stoffen, bijvoorbeeld voor aluminium, grafiet, diamant, ijzer en
goud (één stof is voldoende).
Voor aluminium met dichtheid 2,7x 103 kg/m3. Het aantal atomen in een m3 is dan 2,7 x 103
gedeeld door de atoommassa en die is 27u dat wordt: 6,02 x 1028. Dus bijna 1029
We kunnen ook de typische L van een atoomdoosje uitrekenen: Per atoom is het volume dus 10–6
m3/6,02 x 1022=1,66x10–29. Dit volume is de ribbe van het doosje tot de derde macht. De ribbe is
dus
3
1, 66 x1029  3, 2 x1010 m dat is iets groter dan de straal van een echt aluminium atoom.
9. Energieomzettingen komen tot stand doordat krachten arbeid verrichten en ze bepalen de
snelheid waarmee omzettingen plaatsvinden. Krachten kunnen zelf in feite gedefinieerd
worden als impulsverandering per seconde.
a) Ga na dat dit klopt met de tweede wet van Newton.
Impulsverandering is direct gekoppeld aan de verandering van de kinetische energie.
b) Leid de formule P=Fv voor het mechanisch vermogen af door de formule Ekin = p2 /2m
voor de kinetische energie te differentiëren naar de tijd. (Ga hierbij uit van een beweging
in één dimensie, zodat we de factor cos α kunnen vermijden.
Antwoord: 2de wet: F=ma = mdv/dt = dmv/dt (neem aan m is constant) = dp/dt
p2
d
dE
2 p dp p
mv
P  kin  2m 
 F
F  Fv
dt
dt
2m dt m
m
10. Leg uit wat het verband is tussen de energie van de grondtoestand en de ionisatie-energie van
het waterstofatoom.
De ionisatie energie is de energie die moet worden toegevoerd aan een deeltje in de
grondtoestand om het te bevrijden uit het atoom. Je kunt zeggen dat de totale energie van het
deeltje in de grondtoestand gelijk is aan minus de ionisatie energie, dus:
Etotaal  E p  Ek   Eionisatie
Etotaal  E p  Ek   Eionisatie