Tentamen GM 2011 v final

3NC20 Gecondenseerde materie 2011
Tentamen, 12 april 2011
Algemeen: Beargumenteer je antwoorden. Vermeld zowel de gebruikte basisformules als
de tussenstappen in de afleiding.
Mogelijk te gebruiken formules:
1
.
exp[(   ) / k BT ]  1
1
De Bose-Einstein verdelingsfunctie: n( E ) 
.
exp[ / k BT ]  1
Beoordeling:
Maximaal 80 punten = P. Eindcijfer = P / 8.
________________________________________________________________________
De Fermi-Dirac verdelingssfunctie: f ( E ) 
Opgave 1 (totaal 25 punten)
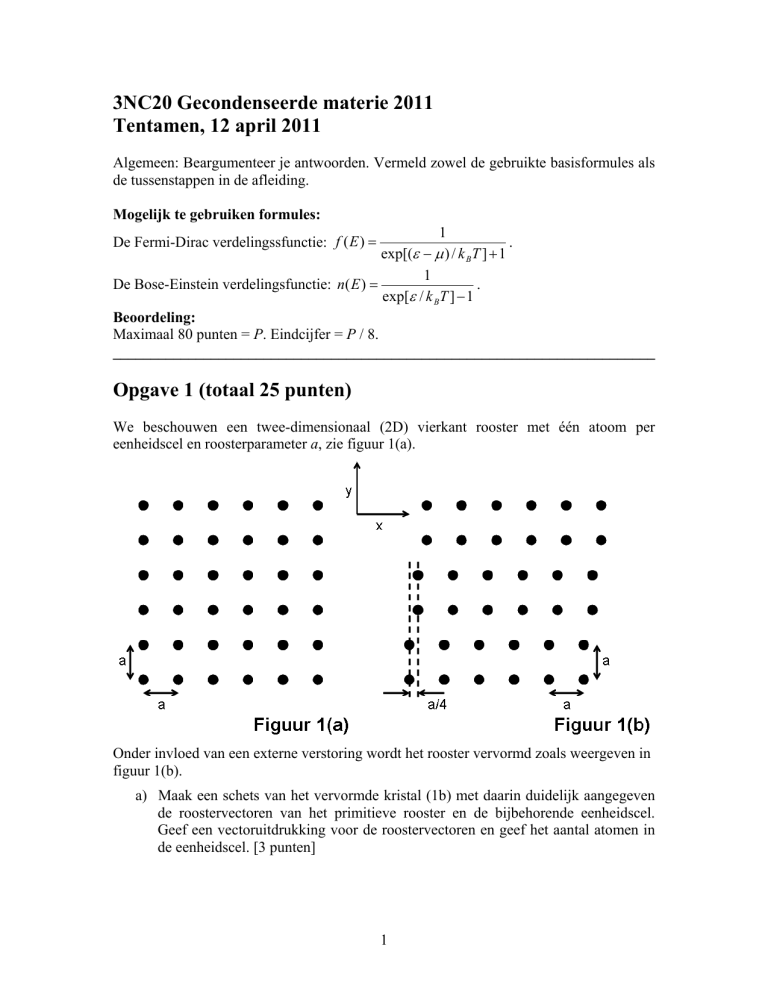
We beschouwen een twee-dimensionaal (2D) vierkant rooster met één atoom per
eenheidscel en roosterparameter a, zie figuur 1(a).
Onder invloed van een externe verstoring wordt het rooster vervormd zoals weergeven in
figuur 1(b).
a) Maak een schets van het vervormde kristal (1b) met daarin duidelijk aangegeven
de roostervectoren van het primitieve rooster en de bijbehorende eenheidscel.
Geef een vectoruitdrukking voor de roostervectoren en geef het aantal atomen in
de eenheidscel. [3 punten]
1
b) Construeer het reciproke rooster (behorende bij figuur 1(b)). Geef een


vectoruitdrukking voor de reciproke roostervectoren b1 en b2 , en teken ze in een
schets van het reciproke rooster. [5 punten]
c) Construeer en schets de eerste Brillouinzone (behorende bij figuur 1(b)). [3
punten]
Vervolgens beschouwen we weer het onvervormde kristal (figuur 1(a)).
We gaan nu de elektronische bandenstructuur voor dit onvervormde, vierkante kristal
uitrekenen met behulp van de tight-binding benadering. Daartoe wordt één s-orbitaal per
atoom meegenomen in de berekening. De atomaire golffunctie wordt genoteerd als
 

s j   (r  r j ) voor atoom j op positie r j . De Hamiltoniaan H wordt beschreven door de
matrixelementen  0  s j H s j en t  s j H s j ' , waarbij j en j’ indices van buuratomen
zijn. Het kristal bevat N atomen. Let op, het matrixelement t is negatief.


d) Geef een algemene uitdrukking voor de golffunctie met golfgetal k ,  k (r ) ,

binnen de tight-binding benadering in termen van k , de atomaire golffuncties
 
 (r  r j ) en N. Zorg daarbij voor de juiste normalisatie. [2 punten]
e) Leidt een uitdrukking af voor de bandenstructuur binnen de tight-binding
benadering. Laat voldoende tussenstappen zien in je afleiding. [8 punten]
 
Figuur 1(c) geeft een schets van de atomaire golffunctie  (r  r j ) voor posities op de
aangegeven gestreepte lijn als functie van de x-coördinaat. De atomaire golffuncties zijn
reëel.
f) Schets de golffunctie (zowel de reële en imaginaire amplitude!) behorende bij de
elektronische toestand met k x   / 2a en k y  0 , voor posities op de gestreepte
lijn met x tussen 0 en 4a. [4 punten]
2
Opgave 2 (totaal 30 punten)
We beschouwen een één-dimensionaal (1D) di-atomair kristal, bestaande uit atomen A en
B met massa resp. MA en MB. De afstand tussen buuratomen is a. We beschrijven
longitudinale roostergolven in het kristal door middel van een massa-veer-beschrijving
met veerconstante f. De uitwijking t.o.v. de evenwichtspositie van atomen A en B in
eenheidscel j wordt beschreven door resp. uj en vj, zie figuur 2(a).
a) Geef de bewegingsvergelijking voor atomen A en B in eenheidscel j. [5 punten]
De algemene oplossing voor een toestand met golfgetal K, wordt gegeven door
u j (t )  u exp(2ijKa ) exp(it ) en v j (t )  v exp(2ijKa ) exp(it ) .
b) Geef de roostervector van het primitieve rooster en geef de waarde van K op de
rand van de eerste Brillouinzone [3 punten]
c) Bepaal de hoekfrequentie  behorende bij de oplossingen van
bewegingsvergelijking op de rand van de eerste Brillouinzone. [5 punten]
de
d) Schets de fononbandenstructuur voor het geval M B   op het interval
  / a  K   / a . Licht je antwoord toe. [3 punten]
e) Schets de fononbandenstructuur voor het algemene geval M A  M B en voor het
geval M A  M B in één en dezelfde figuur, en wederom op het interval
  / a  K   / a . Licht je antwoord toe. [3 punten]
Vervolgens berekenen we de diëlektrische respons van de keten onder invloed van een
homogeen elektrisch veld. De atomaire polarizabiliteit van atomen A en B wordt gegeven
door resp. A en B. Voor het geïnduceerde atomaire dipoolmoment p van een geïsoleerd
atoom in een elektrisch veld E geldt p  E . De atomaire dipoolmomenten worden
beschouwd als een punt-dipool, waarvoor het veld beschreven wordt door de bekende
  3( p  r )r  r 2 p

, voor het veld op positie r gemeten t.o.v. de positie van
formule E (r ) 
5
4 0 r

de dipool. We leggen een elektrisch veld Eext aan loodrecht op de as van het 1D kristal.
We verwaarlozen de invloed van dipoolvelden op afstanden r  2a , d.w.z., alleen
nabuurinteracties worden in beschouwing genomen


f) Bepaal de geïnduceerde dipoolmomenten p A en p B , behorende bij atoom A en
B, resp., uitgedrukt in (o.a.) , B en a. [5 punten]
3
De lineaire keten blijkt zich te gedragen als een halfgeleider. De elektronische
bandenstructuur van de valentieband wordt gegeven door  (k )  V cos(2ka)  1 en de
bandenstructuur van de geleidingsband door  (k )  U  W cos(2ka) , waarin U, V en W
positieve constanten met dimensie energie, en met V  W en U  W .
g) Schets de energiebanden en leid een uitdrukking af voor de effectieve massa van
de elektronen aan de onderkant van de geleidingsband en gaten aan de bovenkant
van de valentieband, uitgedrukt in gegeven parameters en natuurconstanten. [3
punten]
Het optische absorptiespectrum van de 1D halfgeleider staat schematisch weergegeven in
de bovenstaande figuur 2(b).
h) Verklaar het absorptiespectrum. Geef daarbij de waarde van 1 en  2 ,
uitgedrukt in gegeven parameters en natuurconstanten. [3 punten]
Opgave 3 (totaal 25 punten)
We beschouwen een twee-dimensionaal metallisch systeem met macroscopische
afmeting L  L . Het metaal heeft een vierkant rooster met 1 atoom per eenheidscel en
roosterparameter a. De (volledig gevulde) valentie band en (deels gevulde)
geleidingsband worden beschreven met een (2D) vrije elektronen model. De effectieve
massa in zowel de valentieband als in de geleidingsband is m0. De bandgap tussen
valentie- en geleidingsband is Eg, waarvoor geldt dat Eg van de orde van enkele eV’s is.
De Fermi-energie wordt gegeven door EF,0, gemeten t.o.v. de onderkant van de
geleidingsband.
a) Bereken de toestandsdichtheid in de reciproke ruimte, g(k), d.w.z. het aantal
toestanden per oppervlakte-eenheid in de reciproke ruimte. Ga hierbij uit van
periodieke randvoorwaarden. [3 punten]
b) Bereken de elektronendichtheid n (d.w.z. aantal elektronen per oppervlakteeenheid) in de geleidingsband, uitgedrukt in gegeven parameters en
natuurconstanten. [4 punten]
c) Bereken de toestandsdichtheid als functie van energie D(E) in de geleidingsband.
[4 punten]
4
Vervolgens beschouwen we de elektronische warmtecapaciteit van dit metaal. Daartoe
benaderen we de Fermi-Dirac functie door: f ( E )  1 als E  E F  k BT , f ( E )  1 / 2 als
E F  k BT  E  E F  k BT , en f ( E )  0 als E  E F  k BT . We nemen aan dat
E F , 0  k BT .
d) Beredeneer waarom de elektronen in de valentieband bij kamertemperatuur niet
bijdragen aan de warmtecapaciteit [2 punten]
e) Leid op basis van de benadering voor f(E) een uitdrukking af voor de
elektronische warmtecapaciteit van dit metallische systeem, uitgedrukt in o.a. T
en EF,0. (Hint: bereken eerst de totale energie U0) [7 punten]
Tenslotte zoeken we een relatie tussen de elektronische warmtegeleiding en elektrische
ne 2
geleiding van dit metaal. De elektrische geleidbaarheid wordt gegeven door:  
,
m
waarin de betekenis van de parameters als bekend wordt verondersteld. De parameter 
mag in het vervolg van de opgave als bekende constante worden verondersteld.
Voor de warmtegeleidingscoëfficiënt maken we gebruik van de analogie met fononen,
waarvoor de warmtegeleidingscoëfficiënt wordt gegeven door: K  12 Cv v (voor een 2D
systeem).
f) Leid een uitdrukking af voor het elektronische deel van de thermische
geleidbaarheid van dit metaal, uitgedrukt in gegeven parameters en
natuurconstanten. [3 punten].
Het beroemde resultaat van Wiedermann en Franz kan worden geschreven als:
K el /   LT , waarin L het zogenaamde Lorentzgetal.
g) Vind binnen de in dit vraagstuk gehanteerde benaderingen een uitdrukking voor
het Lorentzgetal. [2 punten]
EINDE TENTAMEN
5