HerTentamen GM 2011 final

3NC20 Gecondenseerde materie 2011
Hertentamen, 28 juni 2011
Algemeen: Beargumenteer je antwoorden. Vermeld zowel de gebruikte basisformules als
de tussenstappen in de afleiding.
Mogelijk te gebruiken formules:
1
.
exp[(   ) / k BT ]  1
1
De Bose-Einstein verdelingsfunctie: n( E ) 
.
exp[ / k BT ]  1
Beoordeling:
Maximaal 75 punten = P. Eindcijfer = P / 7.5.
________________________________________________________________________
De Fermi-Dirac verdelingssfunctie: f ( E ) 
Opgave 1 Moleculair kristal (totaal 30 punten)
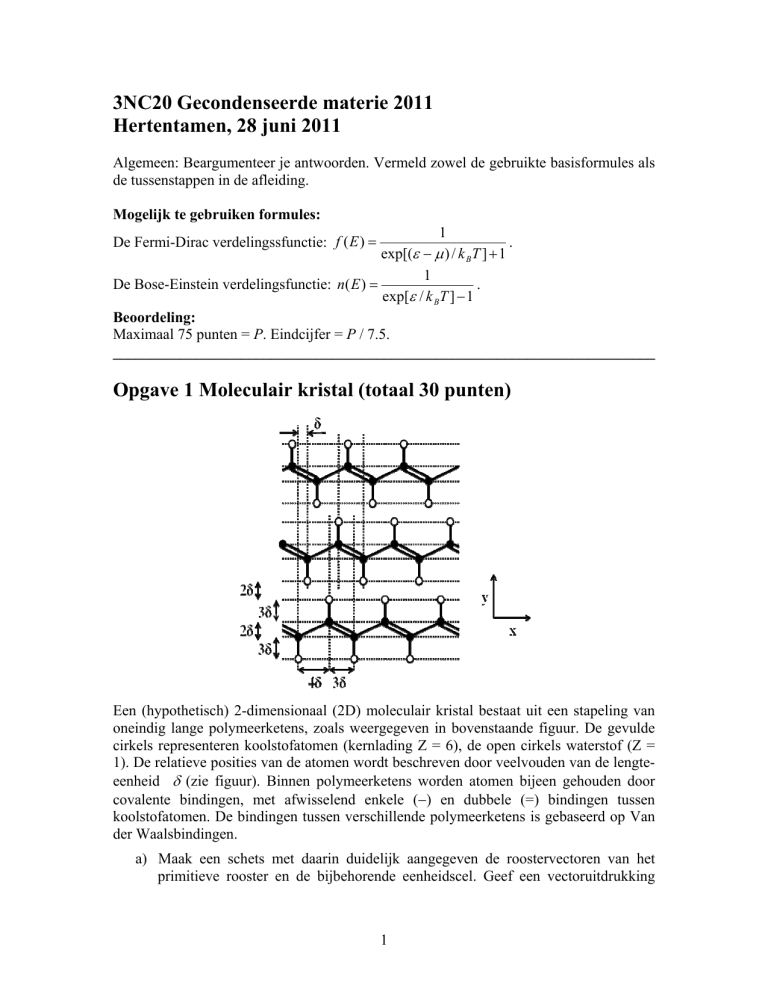
Een (hypothetisch) 2-dimensionaal (2D) moleculair kristal bestaat uit een stapeling van
oneindig lange polymeerketens, zoals weergegeven in bovenstaande figuur. De gevulde
cirkels representeren koolstofatomen (kernlading Z = 6), de open cirkels waterstof (Z =
1). De relatieve posities van de atomen wordt beschreven door veelvouden van de lengteeenheid  (zie figuur). Binnen polymeerketens worden atomen bijeen gehouden door
covalente bindingen, met afwisselend enkele () en dubbele (=) bindingen tussen
koolstofatomen. De bindingen tussen verschillende polymeerketens is gebaseerd op Van
der Waalsbindingen.
a) Maak een schets met daarin duidelijk aangegeven de roostervectoren van het
primitieve rooster en de bijbehorende eenheidscel. Geef een vectoruitdrukking
1
voor de roostervectoren en geef het aantal koolstof- en waterstofatomen in de
eenheidscel. [5 punten]
b) Construeer het reciproke rooster van het moleculaire kristal. Geef een


vectoruitdrukking voor de reciproke roostervectoren b1 en b2 , en teken ze in een
schets van het reciproke rooster. [5 punten]
Er wordt
golfvector
 
e x  e y en
een Röntgendiffractie-experiment uitgevoerd aan dit kristal, waarbij de
van de invallende en gediffracteerde Röntgenstraling gericht is langs resp.
 
ex  e y .
c) Geef een uitdrukking voor de grootste golflengte waarvoor in deze configuratie
een diffractiepiek optreedt. [3 punten]
 
De definitie van de structuurfactor is S G   f j exp(ir j  G ) , waarbij je verondersteld
j
wordt de betekenis van de daarin voorkomende symbolen te kennen of te kunnen
reconstrueren.
d) Geef een uitdrukking voor de structuurfactor voor het in onderdeel c) beschreven
diffractie-expriment. Je mag daarbij de gangbare relatie tussen atomaire
vormfactor en aantal elektronen in een atoom gebruiken. [4 punten]
We gaan nu de elektronische bandenstructuur voor dit moleculaire kristal berekenen met
behulp van de tight-binding benadering. We beperken ons in eerste instantie tot kvectoren in de x-richting. Daartoe berekenen we de 1-dimensionale bandenstructuur van
een enkele polymeerketen bestaande uit N eenheidscellen. Er wordt één pz-orbitaal per
koolstofatoom meegenomen in de berekening en de waterstoforbitalen worden buiten
 
beschouwing gelaten. De atomaire golffuncties worden genoteerd als p q , j   (r  rq , j )

voor atoom q in eenheidscel j op positie rq , j . De Hamiltoniaan H wordt beschreven door
de matrixelementen  0  pq , j H p q , j , t  p q , j H p q ', j '
voor indices q, j, q’ en j’
dusdanig dat zij een enkele binding beschrijven, en T  p q , j H p q ', j ' voor dubbele
bindingen. Let op, de matrixelementen t en T zijn negatief.
e) Geef een algemene uitdrukking voor de component van de golffunctie op atoom q

met golfgetal kx, q, k x   q ,k x (r ) . Doe dit binnen de tight-binding benadering in
 
termen van kx, de atomaire golffuncties  (r  rq , j ) en N. Zorg daarbij voor de
juiste normalisatie. [2 punten]
f) Leid een uitdrukking af voor de matrixelementen q, k x H q ' , k x voor alle
mogelijke combinaties van q en q’ binnen de eenheidcel. Laat voldoende
tussenstappen zien in je afleiding. [7 punten]
Op basis van de berekening onder f) is af te leiden dat de energie als functie van kx wordt
gegeven door  0  T 2  t 2  2tT cos(k x a ) , waarin a bepaald wordt door het juiste
2
antwoord onder f). Tenslotte beschouwen we de volledige twee-dimensionale
bandenstructuur.
g) Bovenstaande figuur schetst de energiedispersie E(k) vanuit het centrum van de
Brillouinzone naar de rand van de Brillouinzone langs de x-as en langs de y-as.
Verklaar de energiedispersie langs de y-as (rechter diagram) [2 punten]
h) Schets hoe het verloop is van de energiedispersie voor het geval t = T; verklaar je
antwoord. [2 punten]
Opgave 2 – 2D Debye model (totaal 20 punten)
We beschouwen een 2D kristal met lengte en breedte L, één atoom per eenheidscel en een
vierkant rooster met roosterconstante a. We benaderen de fonondispersie door   vK ,
waarin  de frequentie, K het golfgetal en v een constante. Houd rekening met het feit dat
de atomen in drie dimensies kunnen bewegen, dus dat er meerdere modes per K-punt
mogelijk zijn. Al deze modes worden verondersteld dezelfde dispersie te hebben. We
gaan de soortelijke warmte uitrekenen volgens het Debye model.
a) Bepaal de toestandsdichtheid als functie van frequentie, D(). [5 punten]
b) Bepaal de Debye frequentie D en het bijbehorende golfgetal kD. [3 punten]
c) Geef een uitdrukking voor de totale thermische energie U in het systeem in
integraalvorm, uitgedrukt in termen van T, D, L, a en natuurconstanten. NB: Je
hoeft je resultaat dus niet te integreren. [3 punten]
d) In de limiet k BT   D geldt dat de soortelijke warmte gegeven wordt door
CV  T p . Bepaal de waarde van p voor deze 2D situatie. (NB: Er wordt niet
gevraagd een expliciete berekening van alle voorfactoren te doen!) [5 punten]
e) De fonondispersie van twee materialen, A en B, wordt beschreven door het 2D
Debye model zoals hiervoor behandeld. Materiaal A heeft een 4 maal zo kleine
Debye frequentie als materiaal B. Maak een schets van de soortelijke warmte van
materiaal A en B in dezelfde grafiek, en geef daarin duidelijk het gedrag in
verschillende limieten aan. [4 punten]
3
Opgave 3 – Halfgeleiders en vrije elektronen (totaal 25 punten)
Beschouw een vierkante, dunne plak van een halfgeleider met lengte en breedte L,
bandgap Eg, elektronenmassa me en gatenmassa mh. In eerste instantie veronderstellen we
dat me  mh . De halfgeleider is zo dun dat deze mag worden beschouwd als een
kwantumput, dat wil zeggen dat er slechts 2 vrijheidsgraden bestaan voor de beweging
van de ladingsdragers, namelijk in de x-richting en in de y-richting. We beschrijven
elektronen en gaten binnen de vrije elektronenbenadering en beschouwen eerst een
intrinsieke halfgeleider.
a) Waar ligt de chemische potentiaal in deze intrinsieke halfgeleider? Beredeneer je
antwoord. [2 punten]
b) Op welke manier kan de chemische potentiaal naar een lagere energie worden
geschoven, d.w.z. in de richting van de valentieband? [2 punten]
c) Bereken de toestandsdichtheid voor de elektronen en de gaten in de halfgeleider
kwantumput met roosterafstand a en lengte en breedte L. [4 punten]
d) Bereken het aantal elektronen Ne in de geleidingsband van de intrinsieke
halfgeleider kwantumput bij temperatuur T onder de aanname dat E g  k BT . [3
punten]
e) Bereken de soortlelijke warmte van deze kwantumput (t.g.v. de geëxciteerde
elektronen en gaten) in dezelfde limiet ( E g  k BT ) en toon aan dat het resultaat
2
 Eg 
 N e . [4 punten]
kan worden geschreven als CV  k B 
 k BT 
Vervolgens doteren we de halfgeleider. In de rest van opgave 3 beschouwen we de
situatie dat me  mh . We vergelijken twee situaties; de situatie met een sterke n-dotering
1
2
noemen we N en de situatie met een sterke p-dotering noemen we P. We nemen aan dat
de dotering in beide gevallen leidt tot hetzelfde aantal vrije ladingsdragers, en dat N en P
kunnen worden beschreven als een metallisch systeem met E F  k BT .
4
f) Gevraagd wordt naar de Fermicontour in de reciproke ruimte voor geval N en P;
geef aan welk van de antwoorden A, B of C zoals getekend in bovenstaande
figuur correct is. In de figuur zijn Fermicontouren aangegeven met een gestreepte
lijn en geven grijze gebieden bezette toestanden aan. Verklaar je antwoord. [3
punten]
Er wordt nu op t = 0 een elektrisch veld E aangelegd in de positieve x-richting.
Verstrooiing van elektronen en gaten wordt verwaarloosd. De gemiddelde waarde voor
de golfvector van de elektronen (dan wel gaten) in het systeem op tijdstip t wordt


beschreven door k N (t ) en k P (t ) .


g) Geef een uitdrukking voor k N (t )  k P (t ) en maak een schets van de situatie voor
N en P in de reciproke ruimte op een zeker tijdstip t = t. [4 punten]
Tenslotte wordt op t  t het elektrisch veld uitgeschakeld en nemen we een verstrooiing
van elektronen en gaten door interactie met fononen in beschouwing. De verstrooiing
wordt beschreven door een gemiddelde verstrooiingstijd  , die gelijk is voor elektronen
en gaten.


h) Geef een uitdrukking voor k N (t ) en k P (t ) voor t  t en maak een schets van de
situatie N en P in de reciproke ruimte op een tijdstip t  t   . [3 punten]
EINDE TENTAMEN
5