Werkbladen

Werkblad 1 bij lessenserie Getallen
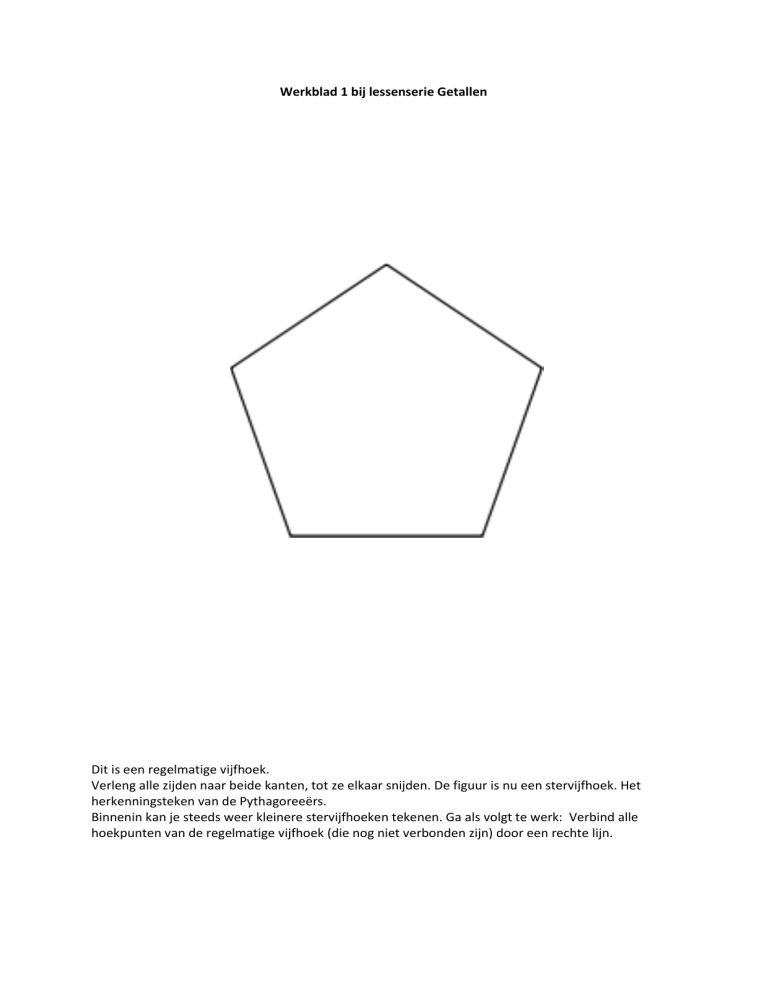
Dit is een regelmatige vijfhoek.
Verleng alle zijden naar beide kanten, tot ze elkaar snijden. De figuur is nu een stervijfhoek. Het
herkenningsteken van de Pythagoreeërs.
Binnenin kan je steeds weer kleinere stervijfhoeken tekenen. Ga als volgt te werk: Verbind alle
hoekpunten van de regelmatige vijfhoek (die nog niet verbonden zijn) door een rechte lijn.
Werkblad 1 bij lessenserie Getallen - vervolg
Bekijk de figuur met vijfsterren hieronder. Een dergelijke figuur heb je zelf hierboven getekend.
De driehoeken die je hierin ziet zijn allemaal gelijkbenig. Alle stompe driehoeken zijn gelijkvormig en
alle scherpe driehoeken zijn gelijkvormig. Alle ‘even grote driehoeken’ zijn congruent. Er geldt dus
bijv. BD’=BE’=E’C = D’A’ en AB = BC’ = BA’ = ED’ en C’D’= D’E’. Dit hoef je niet aan te tonen. Je mag
het aannemen.
We kiezen de eenheid zo klein dat er precies een geheel aantal eenheden past in AB en in BD’. Met
andere woorden, we kiezen 1 zodanig dat AB = een geheel getal en BD’ = een geheel getal. De
verhouding AB:BD’ is dan een breuk.
Twee gehele getallen hebben altijd een grootste gemeenschappelijke deler. Die is minstens 1.
We gaan op zoek naar de grootste gemeenschappelijke deler van AB en BD’.
Hoe vind je die?
De kleinste van de grootste aftrekken geeft: AB-BD’ = ……… = C’D’ (schrijf de tussenstap op)
We hebben dan nu: C’D’ en BD’
Nog een keer de kleinste van de grootste aftrekken geeft:
BD’-C’D’ …………….….= …………………….= D’A” (schrijf de tussenstappen op)
Dus we hebben nu D’A” en C’D’
Kijk naar de zijden waar we mee begonnen. Wat valt je op?
Wat kan je hieruit concluderen?
NB: Het lijnstuk BC’ wordt door D’ verdeeld in twee delen volgens de zogenaamde gulden snede.
Dat betekent dat de twee delen een bijzondere verhouding hebben tot elkaar.
Er geldt namelijk: C’D’/D’B = D’B/C’B
(bonusvraag voor de liefhebber: toon dit aan)
Stel nu C’D’= 1 en BD’= x. Dan geldt x= ½ + ½√5
(bonusvraag voor de liefhebber: toon dit aan)
Antwoordenblad bij werkblad 1 bij lessenserie Getallen (antwoorden zijn in rood)
Twee gehele getallen hebben altijd een grootste gemeenschappelijke deler. Die is minstens 1.
We gaan op zoek naar de grootste gemeenschappelijke deler van AB en BD’.
Hoe vind je die?
 Neem AB en BD’
 Trek de kleinste af van de grootste
 Ga verder met het antwoord en de kleinste
 Trek weer de kleinste af van de grootste
 Herhaal dit tot je twee dezelfde getallen/lengtes hebt.
 Dat is de GGD
De kleinste van de grootste aftrekken geeft: AB-BD’= BC-BD’ = C’D’
We hebben dan nu: C’D’ en BD’
Nog een keer de kleinste van de grootste aftrekken geeft:
BD’-C’D’ = D’B’ –D’E”=E”B’= D’A”
Dus we hebben nu D’A” en C’D’
Kijk naar de zijden waar we mee begonnen. Wat valt je op?
We begonnen met een zijde van de vijfhoek en een zijde van de punt van de ingeschreven ster.
Nu hebben we weer de zijde van een vijfhoek en de zijde van de punt van de ingeschreven ster,
maar dan een stap kleiner.
Wat kan je hieruit concluderen?
We kunnen zo blijven doorgaan. Als we nog twee keer de kleinste van de grootste aftrekken en de
twee kleinsten overhouden, dan vinden we weer de zijde van een vijfhoek en de zijde van de punt
van de ingeschreven ster, maar dan weer een stap kleiner.
Dit houdt nooit op. We zullen nooit twee gelijke getallen krijgen. We zullen nooit een
gemeenschappelijke deler (GGD) vinden.
Maar twee gehele getallen hebben altijd een GGD.
We hadden de eenheid zodanig gekozen dat AB = een geheel getal en BD’ = een geheel getal, maar
dat kan dus kennelijk niet.
Het kan niet zo zijn dat AB en BD’ beiden gehele getallen zijn. AB en BD’ kunnen ook geenbreuken
zijn, want als het breuken waren dan hadden we wel een eenheid kunnen vinden zodanig dat AB en
BD’ geen breuken zijn.
Dus de verhoudingen in het herkenningsteken van de Pythagoreeërs kunnen niet als een breuk
geschreven worden.
Bonusvragen voor de liefhebber:
Maak gebruik van de gelijkvormigheid van de driehoeken in de figuur en van de gelijke lengtes. Los het
bijvoorbeeld zo op:
C’D’=D’E’ en D’B=D’B’=C’A’ => C’D’/ D’B = D’E’/C’A’ |
|
∆D’BE’~∆C’BA’ |
=>
C’D’/D’B = D’B/C’B
Neem nu C’D’= 1 en BD’= x. Dan is C’B = 1+x.
C’D’/BD’ = D’B/C’B => 1/x = x/(1+x) => 1+x = x2 => x2-x-1=0 => x= ½ + ½√5
Werkblad 2 bij lessenserie Getallen
a. Een bewijs dat √𝟐 geen breuk is
We gaan proberen twee gehele getallen a en b te vinden voor de zijden van de gelijkbenige,
rechthoekige driehoek ABC:
C
a
A
a
b
Twee gehele getallen hebben altijd een grootste gemeenschappelijke deler (GGD).
Als de breuk b/a vereenvoudigd is, dan is de GGD = 1.
We gaan op zoek naar de GGD van a en b.
Weet je nog de manier van de Pythagoreeërs om de GGD te vinden?
Kijk anders op het antwoordenblad van werkblad 1.
We beginnen met de twee getallen a en b.
Aftrekken en de twee kleinste overhouden geeft: b-a en a.
Weer aftrekken en de twee kleinste overhouden geeft: ……….. en …………
We kunnen deze getallen als lengtes van lijnstukken in de figuur van de driehoek construeren.
Teken met je passer in de driehoek een boog van de cirkel met middelpunt B en straal BC. Het
snijpunt van deze cirkel met de lijn AB noem je P.
Druk nu de lengtes AP en BP uit in a en b (en schrijf ze in de figuur).
De lengte AP = …………..
De lengte BP = …………..
Teken nu vanuit P een lijn loodrecht op AB naar boven. Het snijpunt van deze lijn met de lijn AC
noem je Q.
We willen nu de lengte PQ uitdrukken in a en b.
B
Die uitdrukking leid je als volgt af:
Je weet dat <QAP=45° en <APQ=90° => <PQA = ……
∆APQ = gelijkb……… => PQ = ………. =
Wat is de lengte van AQ, uitgedrukt in a en b?
Dit leid je als volgt af:
=>
… … … … … … … ..
…………………..
{
𝐵𝑄 = 𝐵𝑄
∆ PQB ≅ ∆ CQB (zhz)
=>
}
𝐶𝑄 = . . … = … … …
{
AQ = a – CQ
} => AQ = …………
Vergelijk de uitdrukking voor AQ en PQ die je hebt gevonden met de uitdrukkingen die je hebt
gekregen na 2 keer aftrekken in het proces om de GGD te vinden.
Als het goed is heb je gevonden dat deze uitdrukkingen gelijk zijn aan elkaar.
We zien:
We begonnen met a en b als rechthoekszijde en schuine zijde van de gelijkbenige rechthoekige
driehoek.
We gingen op zoek naar de GGD van a en b.
Na twee stappen, van twee keer aftrekken, hebben we twee getallen (uitgedrukt in a en b) die gelijk
zijn aan de rechthoekszijde en schuine zijde van een kleinere, gelijkvormige driehoek.
Die twee zijden zijn niet aan elkaar gelijk dus we hebben nog geen GGD gevonden.
We moeten het proces met aftrekken voortzetten.
Probeer in te zien dat als we nog eens twee keer aftrekken dan komen we op twee getallen
(uitgedrukt in a en b) die overeen komen met de rechthoekszijde en schuine zijde van een nog
kleinere gelijkvormige driehoek. Die zijn ook niet gelijk aan elkaar.
Hoe lang we het proces van herhaaldelijk aftrekken ook voortzetten, we zullen op steeds kleinere
getallen komen, maar de getallen zullen nooit gelijk aan elkaar worden. Ze zullen altijd weer (na twee
stappen) overeenkomen met de zijden van een kleinere gelijkvormige driehoek en dus altijd de
verhouding b/a behouden.
Teken de kleinere driehoek die je krijgt na de volgende stap, en ook de nog kleinere driehoek in de
stap daarna.
Conclusie:
We zullen nooit een GGD vinden van a en b.
a en b hebben geen GGD. Ze kunnen dus geen gehele getallen zijn.
b/a is dus geen breuk .
We weten het getal dat de verhouding b/a weergeeft.
Uit de stelling van Pythagoras volgt namelijk:
a2+ a2=b2 => 2a2= b2 => b/a = …..
…….. is dus geen breuk.
b. Benadering van √𝟐
We hebben gezien hoe we allemaal gelijkbenige, rechthoekige driehoeken in elkaar kunnen
construeren, van groot naar steeds kleiner.
Je kan je voorstellen dat je het ook omgekeerd kan doen, je begint bij een heel kleine driehoek en
construeert steeds de grotere. Bij alle driehoeken is de verhouding tussen de schuine zijde en de
rechthoekszijde gelijk, namelijk √2 .
Noemen we de rechthoekszijde en de schuine zijde van de kleinere driehoek a’ en b’ dan geldt:
b’/a’ = b/a = √2
De Pythagoreeërs hebben nu het volgende bedacht: Begin met een heel kleine driehoek, zo klein dat
je alle zijden van deze driehoek 1 kan noemen. We verwaarlozen dus het verschil in de lengte van
deze zijden. En vanaf die allerkleinste driehoek ga je steeds grotere driehoeken bekijken en de
verhouding b/a uitrekenen. Hoe meer stappen je doet, hoe beter je de werkelijke waarde van b/a
benadert.
Hoe vind je de lengten van de zijden van de grotere driehoek (a en b), als je lengtes van de kleinere
driehoek (a’en b’) hebt?
Je weet al dat geldt:
a’= b-a
b’= a-(b-a) = 2a-b
Laat zien dat hieruit volgt:
a=a’+b’
b=2a’+b’
Of in woorden:
-
De rechthoekszijde van de grote driehoek = de schuine zijde + de rechthoekszijde van de
kleine driehoek.
De schuine zijde van de grote driehoek = 2 keer de rechthoekszijde + de schuine zijde van de
kleine driehoek.
Dan kunnen we nu aan de slag.
We beginnen met de kleinste driehoek met schuine zijde = 1 en rechthoekszijde = 1.
Hoe lang zijn de zijden van de driehoek die 1 stap groter is?
rechthoekszijde = 1+1= 2
schuine zijde = 2.1+1 = 3
3/2= 1,5
Maak uit deze driehoek weer een grotere driehoek. Hiervoor geldt:
rechthoekszijde = 2+3= 5
schuine zijde = 2.2+3 = 7
7/5= 1,4
Maak uit deze driehoek weer een grotere driehoek. Hiervoor geldt:
rechthoekszijde = ………..
schuine zijde = ………..
Ga nog minstens 4 stappen verder. Bereken steeds de verhouding b/a en vergelijk dit met de waarde
voor √2 die je op je rekenmachine vindt.
Antwoordenblad bij werkblad 2
Tekst uit het werkblad is gedeeltelijk overgenomen - de antwoorden staan in rood.
.....
C
b-a
Q
a
a-(b-a)
b-a
A
b-a
P
B
Aftrekken en de twee kleinste overhouden geeft: b-a en a.
Weer aftrekken en de twee kleinste overhouden geeft: a-(b-a) en b-a of 2a-b en b-a
….
Druk nu de lengtes AP en BP uit in a en b.
De lengte AP = b-a
De lengte BP = a
Teken nu vanuit P een lijn loodrecht op AB naar boven. Het snijpunt van deze lijn met de lijn AC
noem je Q.
We willen nu de lengte PQ uitdrukken in a en b.
Die uitdrukking leid je als volgt af:
Je weet dat <QAP=45° en <APQ=90° => <PQA = 45° =>
∆APQ = gelijkbenig => PQ = AP = b-a
Wat is de lengte van AQ, uitgedrukt in a en b?
Dit leid je als volgt af:
𝐵𝑃 = 𝐵𝐶 = 𝑎
< 𝐵𝑃𝑄 =< 𝐵𝐶𝑄 = 90°
{
𝐵𝑄 = 𝐵𝑄
{
∆ PQB ≅ ∆ CQB (zhz)
=>
}
𝐶𝑄 = 𝑃𝑄 = 𝑏 − 𝑎
AQ = a – CQ
} => AQ = a-(b-a) =2a-b
Teken de kleinere driehoek die je krijgt na de volgende stap = een van onderstaande figuren
en ook de nog kleinere driehoek in de stap daarna. Bijvoorbeeld onderstaande figuur:
…..
Uit de stelling van Pythagoras volgt namelijk:
a2+ a2=b2 => 2a2= b2 => b/a = √2
√2 is dus geen breuk.
b. Benadering van √𝟐
Laat zien dat hieruit volgt: (dit doe je op de manier van het oplossen van twee vergelijkingen met
twee onbekenden)
a=a’+b’
b=2a’+b’
rechthoekszijde = 5+7 = 12
schuine zijde = 10+7=17
17/12 = 1,41666667
Maak uit deze driehoek weer een grotere driehoek. Hiervoor geldt:
rechthoekszijde is 12+17= 29
schuine zijde = 2.12+17 = 41
41/29= 1,4137931
etc
Werkblad 3 bij lessenserie Getallen
Opdracht 1 aftelbaar oneindig.
Een verzameling die gelijkmachtig is met de natuurlijke getallen N heet een aftelbaar oneindig. Je
kunt dan een één-op-één afbeelding met de natuurlijke getallen maken. Anders gezegd: je kunt de
elementen, net als de natuurlijke getallen, op een oneindig lange rij zetten en ze dan zover aftellen
als je maar wilt. Je komt met aftellen alleen nooit bij het einde.
Voorbeelden:
Z is aftelbaar oneindig.
N
0
1
2
3
4
5
6
7
8
9 10 ...
Z
0
1 -1 2 -2 3 -3 4 -4 5 -5 ...
De verzameling van alle kwadraten is aftelbaar oneindig
N
0
1
2
3
4
5
6
7
...
kwadraten
0
1
4
9
16
25
36
49
...
De volgende verzamelingen zijn allemaal aftelbaar oneindig. Laat zien hoe je de elementen op een
rijtje kunt zetten.
a) De verzameling van alle natuurlijke behalve 5 en 8.
b) De verzameling van alle veelvouden van 1000 (ook de negatieve).
c) De verzameling van alle rationale getallen. Deze is moeilijk. Als het niet lukt zoek dan op
internet of je een oplossing kunt vinden. Wel eerst zelf proberen!
Z.O.Z.
Opdracht 2 Kommagetallen
In de volgende les gaan we bekijken of de R ook aftelbaar oneindig is. Deze opdracht is daar een
voorbereiding op. We kijken naar getallen met 0 voor de komma en 4 cijfers achter de komma zoals
bijvoorbeeld 0.4519, 0.0300 en 0.9988. Noem zulke getallen voor het gemak even komma-4 getallen.
a) Hoeveel komma-4 getallen betsaan er?
We kijken naar de verzameling A = { 0.4543, 0.7000, 0.3245, 0.4507 } waar vier komma-4 getallen
inzitten en gaan op zoek naar een komma-4 getal dat niet in A zit. Hieronder zijn de elementen van A
precies recht onder elkaar gezet.
0.4 5 4 3
0.7 0 0 0
0.3 2 4 5
0.4 5 0 7
0._ _ _ _
b) Vul op de plekken onder de streep steeds een 0 of een 1 in op zo'n manier dat je onder de
streep een getal krijgt dat niet in A zit.
c) Is A gelijkmachtig met de verzameling { 0, 1, 2, 3 } van alle natuurlijke getallen onder de 4?
Leg uit waarom.
We kijken nu naar de verzameling B = { 0.4xxx, 0.x0xx, 0.xx3x, 0.xxx5 }. B is een verzameling van vier
komma-4 getallen alleen je weet niet precies welke vier komma-4 getallen. Van elk getal in B weet je
maar één van de vier cijfers achter de komma. De cijfers achter de komma die je niet kent zijn
vervangen door een x. B zou dus { 0.4567, 0.9012, 0.1234, 0.2345 } kunnen zijn maar B zou
bijvoorbeeld even goed { 0.4111, 0.2022, 0.3333, 0.4445 } kunnen zijn. Dat weet je niet.
d) Kun je een komma-4 getal bedenken dat zeker niet in B zit?
e) Vul op de stippellijntjes steeds een 0 of een 1 in.
Een getal met als eerste cijfer achter de komma ..., met als het tweede cijfer achter
de komma ..., met als het derde cijfer achter de komma ... en met als het vierde cijfer
achter de komma ... zit zeker niet in B.