rechte hoek - Willem

3.1 Soorten hoeken [1]
Let op:
• Een lijn heeft geen eindpunt;
• Een halve lijn heeft één eindpunt
• Een lijnstuk heeft twee eindpunten;
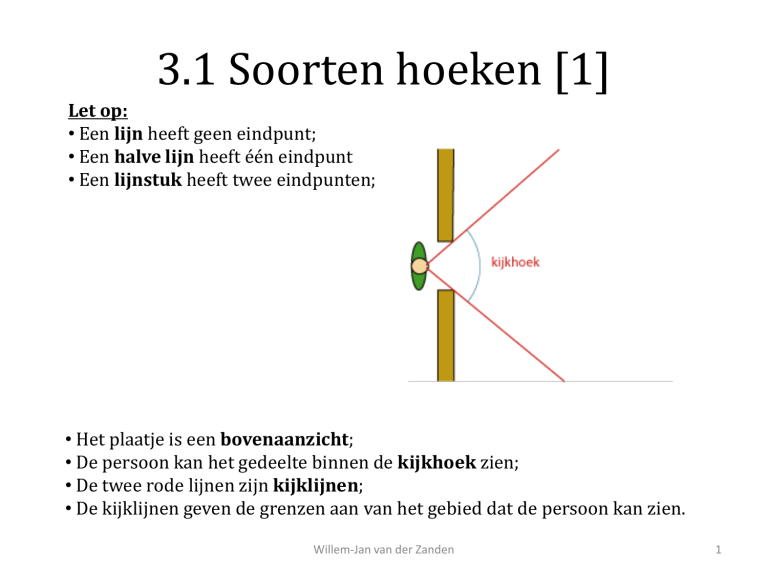
• Het plaatje is een bovenaanzicht;
• De persoon kan het gedeelte binnen de kijkhoek zien;
• De twee rode lijnen zijn kijklijnen;
• De kijklijnen geven de grenzen aan van het gebied dat de persoon kan zien.
Willem-Jan van der Zanden
1
3.1 Soorten hoeken [2]
• Een hoek heeft twee benen (halve lijnen);
• De twee benen komen samen in het hoekpunt.
• Een rechte hoek geef je aan met het symbool ⌝ (Hoek E)
• Een scherpe hoek is kleiner dan een rechte hoek; (Hoek A en C)
• Een stompe hoek is groter dan een rechte hoek; (Hoek B, D en F)
Willem-Jan van der Zanden
2
3.1 Soorten hoeken [2]
• Als beide benen in elkaars verlengde liggen (“rechte lijn”) is het
een gestrekte hoek. Dit is het geval bij hoek D;
• Als je helemaal rond gaat, krijg je een volle hoek. Dit is het geval
bij hoek E.
Willem-Jan van der Zanden
3
3.1 Soorten hoeken [3]
• De grootte van een hoek () wordt aangegeven met graden;
• Een rechte hoek (E )heeft een grootte van 90 graden (90°);
• Een scherpe hoek (A, C ) is dus altijd kleiner dan 90°;
• Een stompe hoek (B, D, F ) is dus altijd groter dan 90°.
Willem-Jan van der Zanden
4
3.1 Soorten hoeken [4]
Om 3 uur heeft de kleine wijzer van de klok
90 graden afgelegd. (Om 12 uur staat de kleine
wijzer recht omhoog)
Om 2 uur heeft de kleine wijzer van de klok
60 graden afgelegd.
Om 1 uur heeft de kleine wijzer van de klok
30 graden afgelegd.
Conclusie:
De kleine wijzer legt in één uur 30 graden af.
Willem-Jan van der Zanden
5
3.1 Soorten hoeken [4]
Om kwart over twaalf heeft de grote wijzer van
de klok 90 graden afgelegd. (Op het hele uur staat
de grote wijzer recht omhoog)
Om tien over twaalf heeft de grote wijzer van
de klok 60 graden afgelegd.
Om vijf over twaalf heeft de grote wijzer van
de klok 30 graden afgelegd.
Conclusie:
De grote wijzer legt in vijf minuten 30 graden af.
Willem-Jan van der Zanden
6
3.1 Soorten hoeken [4]
Kleine wijzer:
Tijd
1 uur
3 uur
6 uur
12 uur
Graden
30°
90°
180°
360°
Tijd
60 min.
30 min.
10 min.
1 min.
Graden
30°
15°
5°
0.5°
Grote wijzer:
Tijd
5 min
1 min
30 min
60 min
Graden
30°
6°
180°
360°
Willem-Jan van der Zanden
7
3.1 Soorten hoeken [4]
Bereken de hoek tussen de wijzers als
het half 3 is:
Stap 1:
Bereken de afgelegde afstand van de grote wijzer
30 minuten = 180°
Stap 2:
Bereken de afgelegde afstand van de kleine wijzer
2 uur = 2 x 30° = 60°
½ uur = 15°
2½ uur = 60° + 15° = 75°
Stap 3:
Bereken de hoek tussen de twee wijzers.
Hoek tussen wijzers = 180° - 75° = 105°
Willem-Jan van der Zanden
8
3.1 Soorten hoeken [4]
Bereken de hoek tussen de wijzers als
het 18:52 uur (of 6:52 uur) is:
Stap 1 (Grote wijzer):
50 minuten = 10 x 30° = 300°
2 minuten = 2 x 6° = 12°
Afstand grote wijzer = 300° + 12° = 312°
Stap 2 (Kleine wijzer):
6 uur = 6 x 30° = 180°
50 minuten = 5 x 5° = 25°
2 minuten = 2 x ½° = 1°
Afstand kleine wijzer = 180° + 25° + 1° = 206°
Stap 3:
De hoek tussen beide wijzers wordt nu:
312° - 206° = 106°
Willem-Jan van der Zanden
9
3.1 Soorten hoeken [4]
Bereken de hoek tussen de wijzers als het 10:15 is:
Stap 1 (Grote wijzer):
15 minuten = 15 x 6° = 90°
Stap 2 (Kleine wijzer):
10 uur = 10 x 30° = 300°
15 minuten = 15 x ½° = 7½°
Afstand kleine wijzer = 300° + 7½° = 307½°
Stap 3:
De hoek tussen beide wijzers wordt nu:
307½° - 90° = 217½°
De kleinste hoek tussen beide wijzers is nu:
360° - 217½° = 142½°
Let op: De uitkomst moet bij dit soort sommen altijd 180° of kleiner zijn.
Willem-Jan van der Zanden
10
3.2 Hoeken meten en tekenen [1]
Willem-Jan van der Zanden
11
3.2 Hoeken meten en tekenen [2]
Willem-Jan van der Zanden
12
3.3 Hoeken berekenen [1]
• In deze figuur zijn vier hoeken te vinden: S1, S2, S3 en S4.
• De volgende hoeken zijn gestrekte hoeken: S12, S23, S34, S14.
• De volgende hoeken zijn overstaande hoeken: S1 en S3 | S2 en S4.
• Overstaande hoeken zijn even groot: S1 = S3, S2 = S4
Willem-Jan van der Zanden
13
3.3 Hoeken berekenen [1]
Voorbeeld 1:
Bereken S4 als je weet dat S2 = 130°
S4 = S2 (overstaande hoek)
S4 = 130°
Let op: Schrijf op waarom je een bepaalde berekening met een hoek mag doen.
Willem-Jan van der Zanden
14
3.3 Hoeken berekenen [1]
Voorbeeld 2:
Bereken S4 als je weet dat S1 = 50°
S4 = 180° - S1 (gestrekte hoek)
S4 = 180° – 50°
S4 = 130°
Let op: Schrijf op waarom je een bepaalde berekening met een hoek mag doen.
Willem-Jan van der Zanden
15
3.4 Hoeken berekenen in
driehoeken en vierhoeken [1]
Gelijkbenige driehoek:
• 2 gelijke zijden (benen);
• De andere zijde heet de basis;
• 2 gelijke basishoeken;
• De ander hoek heet de tophoek.
Willem-Jan van der Zanden
16
3.4 Hoeken berekenen in
driehoeken en vierhoeken [1]
Gelijkzijdige driehoek:
• 3 gelijke zijden;
• Elke hoek is 60°.
Willem-Jan van der Zanden
17
3.4 Hoeken berekenen in
driehoeken en vierhoeken [1]
Rechthoekige driehoek:
• Eén hoek van 90°.
Gelijkbenige rechthoekige driehoek:
· Alle eigenschappen van een gelijkbenige
driehoek;
· Eén hoek van 90°;
• De twee andere hoeken zijn 45˚.
Willem-Jan van der Zanden
18
3.4 Hoeken berekenen in
driehoeken en vierhoeken [2]
Afspraak:
In elke driehoek is de som van de drie hoeken 180°
Voorbeeld:
A = 30°, B = 80°. Bereken C
C
= 180° - A - B (-som ΔABC)
= 180° - 30° - 80°
= 70°
Let op:
Maak als dat nodig is en schets van de driehoek.
Willem-Jan van der Zanden
19
3.4 Hoeken berekenen in
driehoeken en vierhoeken [2]
Opgave 50:
∠B1
= 180° - ∠B2 (gestrekte ∠)
= 180° - 158° = 22°
∠A
= 180° - ∠B1 - ∠C (∠-som ∆ABC)
= 180° - 22° - 18° = 40°
Opgave 51:
∠B1
= 360° - ∠B3 - ∠B2 - ∠B4 (volle ∠)
= 360° - 140° - 90° - 90° = 40°
∠A + ∠C = 180° - ∠B1 (∠-som ∆ABC)
= 180° - 40° = 140°
∠A = ∠C = (∠A + ∠C)/2 = 140°/2 = 70° (gelijkbenige ∆)
Willem-Jan van der Zanden
20
3.4 Hoeken berekenen in
driehoeken en vierhoeken [3]
Hoekensom vierhoek:
In elke vierhoek is de som van de vier hoeken 360°.
Voorbeeld:
Van een vierhoek ABCD is ∠A = 106°, ∠B = 77° en ∠C = 44°. Bereken ∠D.
∠D
= 360° - ∠A - ∠B - ∠C (∠-som □ABCD)
= 360° - 106° - 77° - 44° = 133°
Willem-Jan van der Zanden
21
3.4 Hoeken berekenen in
driehoeken en vierhoeken [3]
Opgave 58:
∠A1
= 90° - ∠A2 (rechte ∠)
= 90° - 52° = 38°
∠B + ∠C1 = 180° - ∠ A1 (∠-som ∆ABC)
= 180° - 38° = 142°
∠B = ∠C1 = (∠B + ∠C1)/2 (gelijkbenige ∆)
= 142°/2 = 71°
∠C2
= 180° - ∠C1 (gestrekte ∠)
= 180° - 71° = 109°
∠E
= 360° - ∠A2 - ∠C2 - ∠D (∠-som □ACDE)
= 360° - 52° - 109° - 138° = 61°
Willem-Jan van der Zanden
22
3.5 Driehoeken tekenen [1]
Willem-Jan van der Zanden
23
3.5 Driehoeken tekenen [2]
Als je de volgende gegevens van een driehoek hebt, kun je deze driehoek
tekenen:
Geval HZH:
Een zijde en de beide aanliggende hoeken
zijn gegeven.
Geval ZZZ:
De drie zijden zijn gegeven.
Willem-Jan van der Zanden
24
3.5 Driehoeken tekenen [2]
Als je de volgende gegevens van een driehoek hebt, kun je deze driehoek
tekenen:
Geval ZHZ:
Twee zijden en de ingesloten hoek zijn
gegeven.
Geval ZHH:
Een zijde, een aanliggende hoek en de niet-aanliggende hoek zijn gegeven.
Willem-Jan van der Zanden
25
3 Samenvatting
Lijnen en lijnstukken:
• Een lijn heeft geen eindpunt;
• Een halve lijn heeft één eindpunt;
• Een lijnstuk heeft twee eindpunten.
Hoeken:
• Een hoek heeft twee benen en één hoekpunt;
• Een rechte hoek geef je aan met het symbool ⌝ en is 90°;
• Een scherpe hoek is kleiner dan een rechte hoek en is minder dan 90°;
• Een stompe hoek is groter dan een rechte hoek en is meer dan 90°;
• Bij een gestrekte hoek liggen beide benen in elkaars verlengde en is 180°;
• Een volle hoek is een hoek van 360°.
Willem-Jan van der Zanden
26
3 Samenvatting
Klok:
• De kleine wijzer legt in één uur 30 graden af;
• De grote wijzer legt in één uur 360 graden af;
• Bij het berekenen van de hoek tussen de wijzers van de klok:
- Bereken de hoek van de grote wijzer;
- Bereken de hoek van de kleine wijzer;
- Het verschil tussen beide getallen is de gevraagde hoek.
Je moet een hoek kunnen meten en tekenen;
Rekenen met hoeken:
Gebruik hierbij de volgende dingen en schrijf op dat je deze gebruikt.
• Overstaande hoeken zijn even groot;
• Een gestrekte hoek is 180°;
• Een rechte hoek is 90°;
• In elke driehoek is de som van de drie hoeken 180°;
• In elke vierhoek is de som van de vier hoeken 360°.
Willem-Jan van der Zanden
27
3 Samenvatting
Gelijkbenige driehoek:
• 2 gelijke zijden (benen);
• De andere zijde heet de basis;
• 2 gelijke basishoeken;
• De ander hoek heet de tophoek.
Gelijkzijdige driehoek:
• 3 gelijke zijden;
• Elke hoek is 60°.
Rechthoekige driehoek:
• Eén hoek van 90°.
Gelijkbenige rechthoekige driehoek:
· Alle eigenschappen van een gelijkbenige driehoek;
· Eén hoek van 90°.
Willem-Jan van der Zanden
28
3 Samenvatting
Geval HZH:
Een zijde en de beide aanliggende hoeken zijn gegeven.
Geval ZZZ:
De drie zijden zijn gegeven.
Geval ZHZ:
Twee zijden en de ingesloten hoek zijn gegeven.
Geval ZHH:
Een zijde, een aanliggende hoek en de niet-aanliggende hoek zijn gegeven.
Willem-Jan van der Zanden
29