Zelftoets

6 Vwo
Vathorst College
Zelftoets
Hoofdstuk 14
De zelftoets draait wat meer om begrip, dan om rekenen. Houdt er rekening mee dat er in het SE zeker ook besteed
wordt aan het rekenen
1
A
B
C
D
2
Een basketbal met massa 0,4 kg beweegt met een snelheid van 10 m/s. Waardoor kun je hierbij geen golfeffecten
waarnemen?
De snelheid is te klein, bij 1000 m/s zien we mogelijk wel golfeffecten.
De golflengte van de bal is te klein om waar te nemen.
De bal is te licht, bij zwaardere objecten zijn golfeffecten van materie gemakkelijker waar te nemen
De atomen in de bal vormen samen geen kristalstructuur.
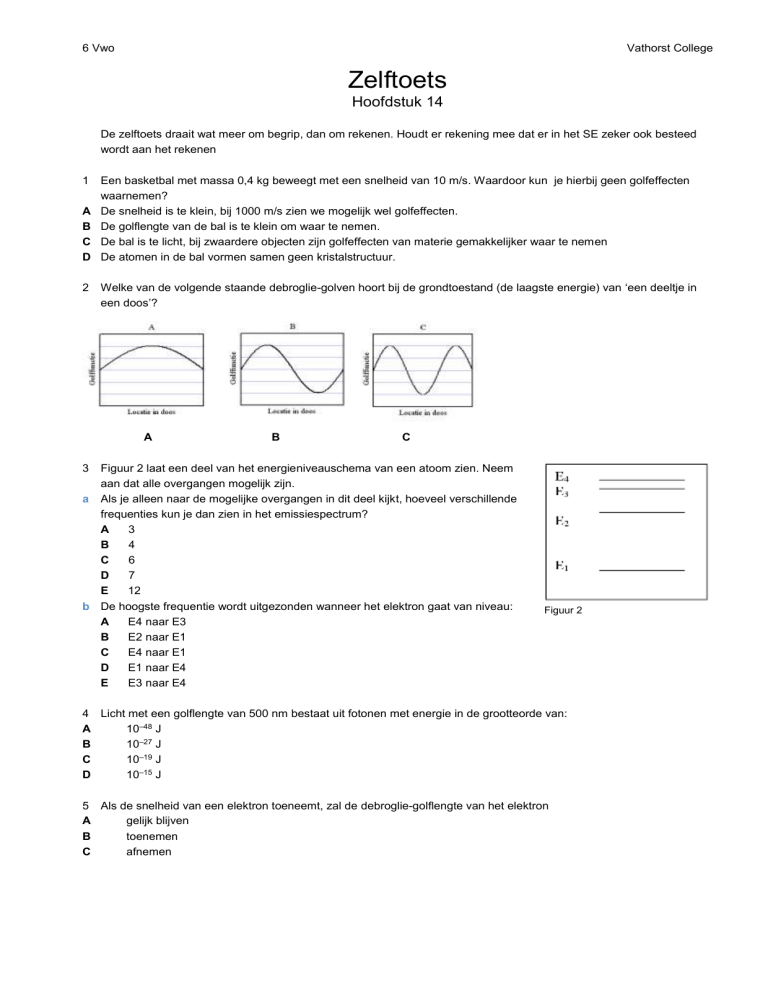
Welke van de volgende staande debroglie-golven hoort bij de grondtoestand (de laagste energie) van ‘een deeltje in
een doos’?
A
B
C
3
Figuur 2 laat een deel van het energieniveauschema van een atoom zien. Neem
aan dat alle overgangen mogelijk zijn.
a Als je alleen naar de mogelijke overgangen in dit deel kijkt, hoeveel verschillende
frequenties kun je dan zien in het emissiespectrum?
A
3
B
4
C
6
D
7
E
12
b De hoogste frequentie wordt uitgezonden wanneer het elektron gaat van niveau:
A
E4 naar E3
B
E2 naar E1
C
E4 naar E1
D
E1 naar E4
E
E3 naar E4
Figuur 2
4 Licht met een golflengte van 500 nm bestaat uit fotonen met energie in de grootteorde van:
A
10–48 J
B
10–27 J
C
10–19 J
D
10–15 J
5 Als de snelheid van een elektron toeneemt, zal de debroglie-golflengte van het elektron
A
gelijk blijven
B
toenemen
C
afnemen
6 Vwo
6
A
B
C
D
7
A
B
C
D
8
A
B
C
D
9
A
B
C
D
Vathorst College
Je hebt een rode laser met een zeer hoge intensiteit en een blauwe laser met een lage intensiteit. Je richt de
laserbundels op een plaatje lithium (in een vacuümbuis). Welke laser heeft de grootste kans om elektronen vrij te
maken uit het lithium?
De rode laser, want de hoge intensiteit kan veel energie overdragen.
De rode laser, want de grotere golflengte van rood licht kan dieper doordringen in het metaal.
De blauwe laser, want de energie per foton is groter dan de uittree-energie.
De blauwe laser, want de golflengte past bij de overgang van de grondtoestand naar de eerste aangeslagen
toestand van het lithium atoom.
De golf-deeltje-dualiteit hangt samen met het begrip debroglie-golven . Zo kan niet voorspeld worden waar
afzonderlijke elektronen zijn, maar een eigenschap van de waarschijnlijkheidsverdeling, beschreven door debrogliegolven, hangt samen met de kans dat een elektron op een bepaalde plek waargenomen kan worden. Welke
eigenschap van de debroglie-golf wordt hier bedoeld?
De amplitudo.
De frequentie.
De trillingstijd.
De golflengte.
Je gaat met behulp van verstrooiing van elektronen aan een grafietkristal de atomaire afstand tussen de
koolstofatomen bepalen. Je meet de verstrooiingshoek voor het maximum van de eerste orde. Welke gegevens van de
elektronen zijn nodig om de atomaire afstand te kunnen bepalen?
De massa en de snelheid.
Alleen de massa.
De massa en de lading.
De lading en de snelheid.
Bij het foto-elektrisch effect worden elektronen uit een metaal vrijgemaakt onder invloed van elektromagnetische
straling. Welke bewering is juist voor het foto-elektrisch effect met betrekking tot de golf-deeltje-dualiteit?
Het effect ondersteunt de deeltjestheorie van licht, want de vrijgemaakte elektronen blijken zich als deeltjes te
gedragen.
Het effect ondersteunt de deeltjestheorie van licht, want de op het metaal vallende straling blijkt zich als
deeltjesstroom te gedragen.
Het effect ondersteunt de golftheorie van licht, want de vrijgemaakte elektronen blijken zich als golven te
gedragen.
Het effect ondersteunt de deeltjestheorie van licht, want de op het metaal vallende straling blijkt zich als golf te
gedragen.
10 In figuur 3 zie je een trillingspatroon van watergolven dat veroorzaakt wordt door
twee kleine trillingsbronnen (boven in het beeld). Een vergelijkbaar patroon is ook te
maken door het licht van een laser op een bepaald voorwerp te laten vallen.
a Met welk voorwerp ontstaat bij laserlicht een vergelijkbaar patroon?
b Leg uit waarom de afstand tussen de twee trillingsbronnen bij laserlicht veel
kleiner moet zijn dan in figuur 3.
Figuur 3
6 Vwo
Vathorst College
11 Figuur 4 laat het interferentiepatroon zien dat ontstaat bij de buiging
van licht aan twee smalle evenwijdige spleten.
a Leg uit waarom dit patroon laat zien dat licht golfeigenschappen
heeft.
Figuur 4
In figuur 5 zie je een schematische tekening van de opstelling.
b Op welke plaats(en) treedt buiging op? Waar treedt interferentie op?
c Beschrijf hoe het patroon verandert als de golflengte van het licht groter
wordt.
Figuur 5
12 Eén van de twee onderstaande stukjes gaat alleen over de golfeigenschappen van elektromagnetische straling, en
maakt geen gebruik van de fotonenergie. Het andere stukje gaat juist vooral over de fotonenergie.
Leg uit welk van de twee stukjes gebruik maakt van het foton en welk niet.
I
In een magnetron wordt straling gemaakt met een frequentie van 2450 MHz. In de ruimte van de magnetron zijn
plaatsen waar de tegen de wanden reflecterende straling zorgt voor extra intensiteit, en er zijn plaatsen waar er juist
minder intensiteit is. Daarom moet het eten ronddraaien, zodat alles even heet wordt. Als je de draaitafel eruit haalt,
kun je een reep chocola er in leggen. De afstand tussen de plekken waar hij snel smelt, is de helft van de golflengte
van de straling. Omdat je ook de frequentie weet, kun je door die afstand te meten de lichtsnelheid bepalen.
II
Er is een gebiedje in het uv-spectrum dat alleen door de stof ozon wordt tegengehouden. De moleculen zijn in staat om
precies de met dat soort uv-straling overeenkomende energie te absorberen. Bij andere stoffen gebeurt dat niet. Als er
geen ozon is, bereikt deze straling de aarde, en dat is schadelijk voor de huid.
13 Fotonen worden ook wel ‘lichtdeeltjes’ genoemd.
a Noem twee deeltjeseigenschappen van fotonen.
b Noem twee eigenschappen waarin fotonen verschillen van materiedeeltjes.
c Noem twee verschijnselen waaruit blijkt dat fotonen ‘lichtdeeltjes’ zijn.
d Leg uit dat fotonenergie iets anders moet zijn dan kinetische energie.
e Noem een voorbeeld waaraan je kunt merken dat bij de ene kleur licht de fotonen meer energie hebben dan bij een
andere kleur.
14 In figuur 6 zie je een interferentiepatroon van golven. Dit patroon kun je gebruiken om het
dubbelspleetexperiment met elektronen te beschrijven.
a Waar bevindt zich dan de dubbelspleet? En waar staat het scherm?
b Worden er midden op het scherm veel of weinig elektronen gedetecteerd?
c Neemt het aantal knooplijnen in dit patroon toe of af als de snelheid van de elektronen
groter wordt gemaakt? Leg uit.
15 De formule voor de debroglie-golflengte geldt ook voor deeltjes die groter zijn dan
elektronen.
a Bereken de debroglie-golflengte van een auto van 1000 kg die met een snelheid van 70
km/h rijdt.
b Maak een schatting van de debroglie-golflengte van een tennisbal na het serveren.
c Leg uit dat in beide situaties geen golfverschijnselen zichtbaar zullen zijn.
Figuur 6
6 Vwo
Vathorst College
16 Ook lading en licht zijn gequantiseerd, net als energie. En ook in deze twee gevallen zijn de quanta heel klein. Een
wasmachine verbruikt een vermogen van ongeveer twee kilowatt.
a Laat met een berekening zien dat er dan een stroomsterkte van ongeveer 9 A door de draden loopt.
b Bereken hoeveel elektronen er per seconde door de draden lopen.
Een gloeilamp die 60 watt verbruikt, zendt ongeveer 3 W aan licht uit. De gemiddelde energie van de fotonen is 2,2 eV.
c Bereken hoeveel fotonen zichtbaar licht de gloeilamp per seconde uitzendt.
17 Als een atoom een foton uitzendt ontstaat er een waarschijnlijkheidsverdeling.
a Met welke snelheid breidt de waarschijnlijkheidsverdeling zich uit?
b Leg in je eigen woorden de betekenis van de waarschijnlijkheidsverdeling uit.
c Wat gebeurt er met de waarschijnlijkheidsverdeling bij detectie van het foton?
d Is het tijdstip waarop het foton wordt uitgezonden een kwestie van toeval of wordt het uitzenden van een foton
bepaald door iets anders?
e De waarschijnlijkheidsverdeling heeft de vorm van een bol. Leg uit wat dat betekent voor de richting waarin het
foton gedetecteerd wordt.
18 Bij een bepaald atoom horen de energieniveaus -9,2 eV, -5,4 eV, -2,7 eV en -1,9 eV.
a Bereken de fotonenergie van de spectraallijnen van dit atoom.
b Ga na welke van de genoemde spectraallijnen in het zichtbare deel van het spectrum
liggen.
19 In figuur 7 en 8 zie je beelden die gemaakt zijn met een Scanning Tunneling Microscope
(STM).
c Leg in je eigen woorden uit dat je de bolletjes op het beeld niet mag zien als foto’s
van atomen.
d Op de beelden zie je ook kleuren. Waar komen die kleuren vandaan?
e Waardoor worden de golfachtige structuren in figuur 8 veroorzaakt?
Figuur 7
20 De uitdrukking ‘een deeltje in een doosje’ gaat over quantumverschijnselen bij deeltjes
die gebonden zijn aan een kleine ruimte.
a Geef twee voorbeelden van deeltjes die gebonden zijn aan een kleine ruimte.
Figuur 8
Als de afmetingen van de ruimte toenemen dan is er op een gegeven moment geen sprake meer van
quantumverschijnselen.
b Hoe weet je of een ruimte groot of klein is voor een deeltje? Waarmee moet je de afmetingen vergelijken?
Een neutron in de kern van een atoom is een deeltje dat beweegt en een de-broglie-golflengte heeft.
c Is de debroglie-golflengte van een neutron in een kern groter of kleiner dan van een elektron in een atoom? Leg uit.
21 De buitenste elektronen van een bepaald type molecuul gedragen zich bij goede benadering als elektronen in een
doosje. Het doosje is 4 nm lang en er bevinden zich 7 elektronen in. In elke quantumtoestand kunnen zich twee
elektronen bevinden.
a Leg uit dat in de grondtoestand één elektron zich bevindt in quantumtoestand n = 4.
b Bereken de totale energie van deze grondtoestand.
De belangrijkste spectraallijn van de stof komt overeen met het verschil tussen de grondtoestand en de eerste
aangeslagen toestand.
c Bereken de golflengte van deze spectraallijn.
22 Een onbekend quantumdeeltje heeft een snelheid van 3,00·10 7 m/s.
a Leg uit waarom dit deeltje geen foton kan zijn.
b Aangenomen dat dit deeltje een elektron is, bereken zijn debroglie-golflengte.
Een ander onbekend deeltje heeft een deBroglie-golflengte van 10 nm.
c Zal dit deeltje merkbaar quantum-gedrag vertonen? Leg uit.