1. Een man van 80kg springt rechtstandig omhoog. Zijn voorvoeten

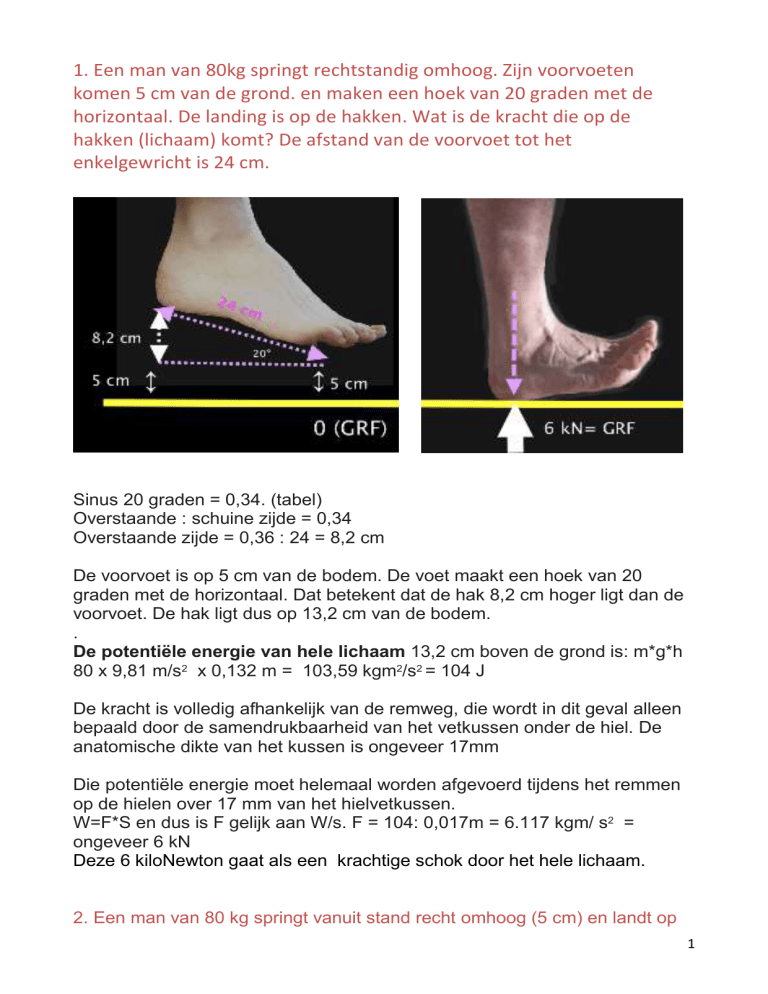
1. Een man van 80kg springt rechtstandig omhoog. Zijn voorvoeten
komen 5 cm van de grond. en maken een hoek van 20 graden met de
horizontaal. De landing is op de hakken. Wat is de kracht die op de
hakken (lichaam) komt? De afstand van de voorvoet tot het
enkelgewricht is 24 cm.
Sinus 20 graden = 0,34. (tabel)
Overstaande : schuine zijde = 0,34
Overstaande zijde = 0,36 : 24 = 8,2 cm
De voorvoet is op 5 cm van de bodem. De voet maakt een hoek van 20
graden met de horizontaal. Dat betekent dat de hak 8,2 cm hoger ligt dan de
voorvoet. De hak ligt dus op 13,2 cm van de bodem.
.
De potentiële energie van hele lichaam 13,2 cm boven de grond is: m*g*h
80 x 9,81 m/s2 x 0,132 m = 103,59 kgm2/s2 = 104 J
De kracht is volledig afhankelijk van de remweg, die wordt in dit geval alleen
bepaald door de samendrukbaarheid van het vetkussen onder de hiel. De
anatomische dikte van het kussen is ongeveer 17mm
Die potentiële energie moet helemaal worden afgevoerd tijdens het remmen
op de hielen over 17 mm van het hielvetkussen.
W=F*S en dus is F gelijk aan W/s. F = 104: 0,017m = 6.117 kgm/ s2 =
ongeveer 6 kN
Deze 6 kiloNewton gaat als een krachtige schok door het hele lichaam.
2. Een man van 80 kg springt vanuit stand recht omhoog (5 cm) en landt op
1
de voorvoeten. De hoek die de voeten t.o.v. de bodem maakt bij de landing is
20 graden. Het draaipunt is de bal van de voeten. De afstand van het BSG
(enkelgewricht) en pees = 6 cm ) en tot bal van de voet is 15 cm
Wat is nu de (excentrische spier)kracht die de kuitspieren opvangen bij de
landing?
Het
lichaam
bevindt
zich nog
steeds op
een
hoogte
van 13,2
cm (5 +
8,2 cm)
door de
hoek die
de voet
maakt..
De potentiële energie van het hele lichaam is m.g.h =
80 kg * 9,81 m/s2 * 0,132m = 103,6 kgm2/s2 = ongeveer 104 Joule.
Het remmen (excentrische spierwerking) begint zodra de bal van de voet de
grond raakt. De energie wordt dan afgevoerd door
a. Het vetkussen onder de voorvoeten: 7 mm en
b. Vervolgens over de afstand van de hiel tot de bodem. Deze is 8,2 cm
In totaal is er een remweg van 8,2 + 0,7 cm = 8,9 cm
De potentiele energie van 104 J moet worden afgevoerd over 0,089 m
F = W/s. F = 104 : 0,089 = 1.168 kgm/s2 =1168 N = ongeveer 1 kN
Moment van krachten.
Fpees x arm = GRF x arm
Fpees x 6 cm = 1.168 x 15 cm
Fpees = 17.520 : 6 = 2.920 kgm/ s2 = 2,9 kiloNewton
Conclusie: de kracht die de achillespees + m triceps surae leveren is
ongeveer 3 kN,
3. Een man van 80 kg springt vanuit stand recht omhoog (5 cm) en landt op
de voorvoeten. De hoek die de voeten t.o.v. de bodem maakt bij de landing is
20 graden.
2
Hoeveel kracht komt er op de achillespees en kuitspieren te staan, wanneer
(in theorie) de hoek van 20 graden gehandhaafd blijft. M.a.w. de enkel buigt
niet (voet en scheenbeen zijn een geheel)
De potentiele energie van 104 J wordt alleen afgevoerd door het vetkussen
onder de bal van de voeten.
De excentrische spierwerking van de kuiten verdwijnt en het wordt als het
ware kaatsen.
De anatomische dikte van het vetkussen onder de bal van de voeten is 7 mm
De potentiele energie van104 J moet worden afgevoerd over 0,007 m
F = W/s. F = 104 : 0,007 = 14857 kgm/s2 =14857 N = ongeveer 15 kN
Moment van krachten.
Fpees x arm = GRF x arm
Fpees x 6 cm = 14857 x 15 cm
Fpees = 222855 : 6 = 37142 kgm/ s2 = 37 kiloNewton
Conclusie:
Zonder de excentrische spierwerking (dorsaalflexie in het BSG) komt er een
kracht van 37 kN op de achillespees + m triceps surae.
Dit is een factor 12 meer dan wanneer dorsaalflexie in het BSG zou optreden,
waarbij de kracht 2,9 kN is
3