III. Atoomstructuur

1
III. Atoomstructuur
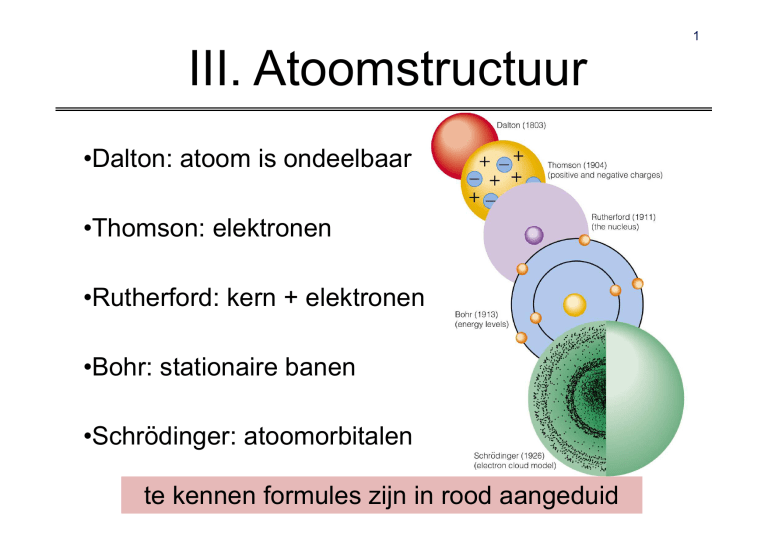
•Dalton: atoom is ondeelbaar
•Thomson: elektronen
•Rutherford: kern + elektronen
•Bohr: stationaire banen
•Schrödinger: atoomorbitalen
te kennen formules zijn in rood aangeduid
2
Atoomspectra &
atoommodel van Bohr
3
Probleem atoommodel van Rutherford
Eelektron = f(r) = Ep + Ekin
Kern: puntlading, q = + Ze
Ep, elektron
0
Ekin
Ze2
Ep = −
4πεor
r
1
= mv 2
2
v
+Ze
θ
r
dθ
v =r
= rω
dt
bewegende elektrische lading straalt continu E uit
⇒ Eelektron↓ continu ⇒ r van cirkelbaan ↓ continu
⇒ elektron zou met kern moeten versmelten????
⇒ in tegenspraak met realiteit
verfijning atoommodel op basis van studie van atoomspectra
licht uitgestraald door ge-ëxciteerde atomen
4
•Licht
•elektromagnetische golven
•golflengte en amplitude
•lichtquanta of fotonen
•elektromagnetisch spectrum
•wit licht
•atoomspectra
•Atoommodel van Bohr
•verklaring atoomspectra
5
Licht
6
Golf
•gekarakteriseerd door golflengte λ en amplitude A
golflengte λ
amplitude A
golflengte: λ [m]
•breidt zich periodisch uit in ruimte en tijd
voortplantingsnelheid: v [ms-1]
frequentie: ν
[s-1
of Hz]
Griekse letter nu
v
ν = ⇒ v = λ×ν
λ
7
golf breidt periodisch uit in ruimte & tijd
t geluid =
10000 m
= 29 s
−1
340 ms
t licht
10000 m
−5
=
=
3
×
10
s
8
−1
3 × 10 ms
8
Licht = elektromagnetische straling
c
ν = ⇒ c = λ×ν
λ
c: lichtsnelheid
λ↓ ⇒ ν↑
Elektromagnetisch spectrum
9
10
infraroodstraling
UV-straling
γ-straling
microgolven
•Radiogolven: golflengte radiostation dat uitzendt op 107.6 MHz
107.6 MHz = 107.9 × 10 6 Hz = 107.6 × 10 6 s −1
c
3 × 10 ms
λ= =
ν 107.6 × 10 6
8
-1
s
-1
= 2.79 m
11
•kleur zichtbaar licht wordt bepaald door golflengte
• wit licht: mengsel van alle
kleuren van zichtbaar licht
12
Voorbeeld 1
Bereken de golflengten van de laserpointers die
licht van volgende frequentie uitstralen:
5.75 × 1014 s-1
4.84 × 1014 s-1
4.27 × 1014 s-1
522 nm ⇒ groen
620 nm ⇒ oranje
703 nm ⇒ rood
13
14
Licht bestaat uit lichtquanta of fotonen
hc
E =h×ν =
λ
h = 6.626 × 10-34 Js; Planck constante
λfoton↓ ⇒ Efoton↑
A↑⇒ intensiteit (helderheid) licht↑
EA < EB < EC
15
Voorbeeld 2
Bereken de energie van een foton in geel
licht met een frequentie van 5.2 ×1014 s-1.
E foton = 3.4 × 10 −19 J
16
17
Voorbeeld 3
Bereken het aantal fotonen in een laserpuls
met golflengte 337 nm en een totale energie
van 3.83 mJ.
Nfotonen = 6.5 × 1015
18
Spectrum van zonlicht (wit licht)
•continu spectrum: alle kleuren zijn aanwezig
•alle golflengten van zichtbaar licht zijn aanwezig
c
•continuüm van energieën E = h ×
λ
19
20
Atoomspectrum van waterstof
geëxciteerde H-atomen
λ foton =
656 nm =
•lijnenspectrum; spectraallijnen
•enkel welbepaalde golflengten zijn aanwezig
•enkel fotonen met welbepaalde energie
hc
E foton,λ
hc
E foton,656 nm
21
Emissie licht: overgangen tussen discrete E-niveau’s
E2
begintoestand: atoom in toestand 2
emissie foton met ν
E1
eindtoestand: atoom in toestand 1
wet van behoud van energie: Eeind = Ebegin
E1 + E foton = E 2
E1 + hν foton = E 2
E2 > E1 ⇒ ∆E2→1 = E1 – E2 < 0: atoom straalt energie
uit als licht met frequentie νfoton
∆E 2→1 = E1 − E 2 = hν foton
E4
E3
E2
22
hc
∆E4→1 = E1 − E4 =
λ4→1
hc
∆E3→1 = E1 − E3 =
λ3→1
hc
∆E2→1 = E1 − E2 =
λ2→1
E1
∆Ei→ j
hc
= E j − Ei =
λ i→ j
•atoom heeft discrete energietoestanden: En
enkel specifieke energieën En mogelijk voor elektron in atoom
energie van elektron in atoom is gequantiseerd
•atoom bezit elektronische structuur
23
elk element bezit karakteristieke set van spectraallijnen
•golflengten spectraallijnen zijn karakteristiek voor atoomsoort
•atoomspectrum hangt af van elektronische structuur atoom
•set discrete energieniveaus En is karakteristiek voor atoomsoort
24
Emissiespectrum en absorptiespectrum
Ei > Ej ⇒ ∆Ei→j < 0 en |∆Ei→j| = hνfoton; atoom straalt energie uit
Ei < Ej ⇒ ∆Ei→j > 0 en ∆Ei→j = hνfoton; atoom neemt energie op
25
Atoommodel van Bohr
26
Verklaring atoomspectra
•Bestaan van stationaire toestanden
•elektron is deeltje met massa me
•elektron beweegt op cirkelvormige baan
•in deze toestand is E elektron = constant
•quantisatievoorwaarde: welbepaalde waarden van r mogelijk
•Frequentievoorwaarde: ∆Ei→ j = E j − Ei = h ν i→ j
hc
=
λ i→ j
Ei : e in stationaire toestand i
emissie E: e van i→j
absorptie E: e van j→i
atoom straalt energie uit
∆Ei→j = Ej - Ei < 0
atoom neemt energie op
∆Ej→i = Ei – Ej > 0
Ej : in stationaire toestand j
27
Toegelaten stralen stationaire baan elektron
rn =
0
n2 . h2 .εo
π. me . Z . e
Ep, elektron
2
n = 1, 2, 3....∞
rn = 5.29 × 10
Ze2
Ep = −
4πεor
r1 r2
r3
r
−11 n
2
Z
1
Ek = m e . v 2
2
2
Z
.
e
v2 =
4π.εo . me . r
⇒ Etot,elektron = f(straal r van stationaire baan)
⇒ enkel specifieke waarden voor Etot,elektron zijn mogelijk
28
Toegelaten energiewaarden elektron in atoom
2
4
Z . e . me
En = −
2 2 2 n = 1, 2, 3....∞
8 ε o .n .h
gebonden toestanden
E∞ = 0 > En
n: hoofdquantumgetal
n = 1 : grondtoestand
n > 1 : geëxciteerde toestanden
⇒ energie elektron in atoom is gequantiseerd
2
Z
−18
[Joule]
En = − 2.18 × 10
n2
Coulombkracht ⇒ e beweegt in potentiaalveld Ep
2
29
2
n . h .εo
rn =
π. me . Z . e2
2
4
Z . e . me
En = −
2 2 2
8 ε o .n .h
Z . e2
Ep = −
4 π.εo . r
elektron kan enkel op stationaire cirkelbanen met welbepaalde straal rn en met
welbepaalde totale energie En langs de wanden van de potentiaalput bewegen
overgangen tussen stationaire toestanden is enkel mogelijk door absorptie of
emissie van straling met welbepaalde frequentie ν
Verklaring emissiespectrum van H
∆Eni →n j = hν ni →n j = En j − Eni = 2.18 × 10
−18
30
 1

1
Z  2 − 2
n

n
j 
 i
2
frequentie van de geëmitteerde straling bij transitie van ni → nj (i > j)
Ionisatie-energie IE
31
voorbeeld: IE van H (n = 1→ n = ∞)
n = ∞; E∞ = 0; Ep = 0; Ekin = 0 (r = ∞; deeltjes in rust)
atoom neemt energie op (∆E > 0)
IE
λfoton
∆E1→∞
hc
= IE =
λ foton
n = 1; E1: e in stationaire toestand 1 (grondtoestand)
2 

(
1
)
−
18
IE = ∆E1→∞ = E∞ − E1 = 0 J −  − 2.18 × 10
J  = 2.18 × 10 −18 J
2 

(
1
)


IE = ∆E1→∞ = 2.18 × 10
−18
J
23 atomen
× 6.022 × 10
= 1300 kJ / mol
atoom
mol
32
∆E = IE = E A +
A(g) → A+(g) + e
( g)
− E A ( g)
ion en elektron op r = ∞ en in rust (v = 0)
hν
e; ve
↑
A(g)
Ebegin = E A( g) + E foton
A+(g)
Eeind = E
A ( g)
wet van behoud van energie:
E A( g) + E foton = E
A + ( g)
+
+ Ee
E foton − E e = E A + ( g ) − E A ( g ) = IE
hc 1
IE = E foton − Ee =
− mv e 2
λ 2
+ Ee
33
Opgave 3.1
Wat is, gebruikmakend van het Bohrmodel, de
straal en de energie van het B4+-ion in de
toestand n = 3?
Wat is de frequentie en de golflengte van het
licht dat door dit ion ge-emitteerd wordt bij
overgang naar de toestand n = 2?
Hoeveel energie is er nodig om de elektronen
van 1 mol B4+-ionen in deze toestand te
r = 95.3 pm
verwijderen?
E = −6.06 × 10 J
3
−18
3
λ 3→2 = 26.3nm
∆E3→∞ = 3.64 × 103 kJ / mol
34
35
Opgave 3.4
Elektronen kunnen versneld worden door
aanleggen van een potentiaalverschil.
Veronderstel een elektron initieel in rust dat
door aanleggen van een potentiaalverschil
versneld wordt zodat λelektron = 10-10m. Hoe
groot is het potentiaalverschil dat dit elektron
doorlopen heeft?
potentiaalverschil = 150 V
36
37
Opgave 3.8
De minimum energie vereist om elektronen van het oppervlak van een
metaal te verwijderen is 270.4 kJ/mol. Wat gebeurt er indien licht met
een golflengte van 461 nm op dit metaal invalt. Verklaar je antwoord.
a) er worden geen elektronen verwijderd
b) er worden elektronen met een energie van 1.8 × 10-20 J geëmitteerd
c) er worden elektronen met een energie van 4.3 × 10-19 J geëmitteerd
d) er worden elektronen met een energie van 7.4 × 10-31 J geëmitteerd
e) er worden elektronen met een onbekende energie geëmitteerd
a: er worden geen elektronen verwijderd
38
39
Opgave 3.42
Bij bestraling van atomen of moleculen met UV-straling
worden valentie-elektronen uit het atoom of de molecule
verwijderd. In foto-elektronspectroscopie wordt gebruik
gemaakt van UV-straling met een bekende frequentie en
wordt de kinetische energie van de uitgestraalde
elektronen gemeten. Aan de hand van deze gegevens
kan, op basis van de wet van behoud van energie, de
ionisatie-energie van atomen en moleculen bepaald
worden. Bij bestraling van rubidiumatomen met UV-licht
met een golflengte van 58.4 nm bedraagt de snelheid van
de uitgestraalde elektronen 2450 km s-1. Bepaal de
ionisatie-energie (kJ/mol) van rubidium.
IE = 403 kJ / mol
40
41
Het quantumechanisch
atoommodel
42
Bohr: cirkelbanen
de Broglie: staande golven
Schrödinger: golffuncties en atoomorbitalen
43
•de Broglie: interpretatie quantisatie straal Bohrse banen
•staande golven
•elektronen hebben staande golfkarakter
•Heisenberg: onzekerheidsprincipe
•welgedefinieerde baan elektron rond kern kan niet
•Schrödinger: het quantummechanische atoommodel
•golffuncties: - quantumgetallen en energie elektron
- probabiliteitsdistributie en atoomorbitalen
•één-elektronsysteem: - energieniveau’s en quantumgetallen
- vorm atoomorbitalen
•meer-elektronsysteem
44
de Broglie
Staande golf
staande golf is beperkt tot een bepaald gebied in de ruimte
knoop
λ
L=n
2
met n = 1, 2, 3…
knoop
knoop: amplitude = 0
knoop
45
Interferentie van golven
Uitdoving indien λ staande golf niet voldoet aan
λ
L=n
2
met n = 1, 2, 3…
46
de Broglie: interpretatie quantisatie r
e: gevangen in elektrisch veld kern
e: beschouwen als staande golf
λe
L=n
2
n . h .ε o
rn =
π. me . Z . e 2
2
2
rn moet geheel veelvoud zijn van λe
n ≠ geheel getal ⇒ uitdoving golf
met n = 1, 2, 3…
47
48
Elektronen hebben staande golfkarakter
•foton
hc
licht E = h × ν =
λ
equivalentie materie-energie E = mc2
hc
h
2
= mc ⇒ λ f oton =
λ
mc
•naar analogie met licht: elektron = materiegolf
snelheid elektron = v
⇒ golfeigenschappen met λ elektron
h
h
=
=
me v p
elektronen hebben staande golfkarakter en worden
gekarakteriseerd door een golflente λe
v: snelheid [m/s]; p: impuls [kg m/s]
golfkarakter macroscopisch object is praktisch
ondedecteerbaar omdat λ té klein is
•elektron in H atoom: m = 9.11 × 10-31 kg; v = 2.2 × 106 ms-1
λ=
6.626 × 10 −34
(9.11 × 10
−31
)
kg m2
s

6 m
kg  2.2 × 10

s

= 3.3 × 10 −10 m
diameter atoom: 10-10m
•bal: m = 120 g; v = 44.7 ms-1
2
kg
m
6.626 × 10 −34
s = 1.24 × 10 −34 m
λ=
m

(0.120 kg)  44.7 
s

diameter bal: 10-2m
49
50
Elektron in H atoom vibreert als staande golf langsheen
cirkelbanen met straal rn die geheel veelvoud zijn van λe
2D voorstelling
staande golf
knoop
1D voorstelling golf
= golffunctie ψi
1D voorstelling ψi2
51
Heisenberg
52
Heisenberg: onzekerheidsprincipe
h
( ∆x ) ( ∆mv ) ≥
4π
onzekerheid positie
onzekerheid snelheid
elektron: ∆mv ≅ 10−25 kgms−1
W. Heisenberg
h
6.626 × 10 −34 J s
−10
( ∆x ) ≥
=
≅ 10 m
− 25
−1
4π( ∆mv ) 4π × 10 kg m s
diameter atoom = 10−10 m
•beschrijving van elektron als deeltje dat welgedefinieerde
baan rond de kern volgt zoals in model van Bohr KAN NIET
•met welke kans kan het elektron in een bepaald gebied van
de ruimte rond de atoomkern aangetroffen worden?
53
Schrödinger: het
quantummechanisch
atoommodel
54
Schrödinger: quantummechanisch atoommodel
quantummechanische beschrijving gedrag elektron in
atoom gebaseerd op staande golfkarakter elektron
Ĥ : Hamiltonoperator
E: bindingsenergie e
ψ: golffunctie
Ĥψ = Eψ
 ∂
∂
∂ 
 2 + 2 + 2  ψ( x, y, z) = ∇ 2 ψ( x, y, z)
∂y
∂z 
∂x
2
2
2
golffunctie
−
h2
8π2me
Mmm… let’s see what
it gives if I try to
describe it as a wave
Etot elektron
∇ 2 ψ( x, y, z ) + V( x, y, z ) ψ( x, y, z ) = E ψ( x, y, z )
Ekin elektron
formules: niet te kennen
Epot elektron
E. Schrödinger
55
Golffuncties: quantumgetallen en energie elektron
golfvergelijking
wiskundige beschrijving staande golfgedrag e in atoom
oplossing
golffuncties Ψi
gekarakteriseerd door: - Eψi : energie e in toestand i
- quantumgetallen n, l, ml
|z| = (a2 + b2)1/2
3D beschrijving staande golfgedrag e in toestand i
bevat eiφ ⇒ e±iφ = cosφ ± i sinφ ⇒ reële functie
in de scheikunde gebruikt
|Ψi|2
probabiliteit om e in toestand i aan te treffen in één
punt op afstand r van de kern (orbitaal)
in de scheikunde spreekt men kortweg van ψi2
complex getal z = a + ib
ψ voor elektron in H-atoom in 1s toestand
56
3
 − Zr 
 1  Z 2

ψ1s = 
   exp 
 π   a0 
 a0 
ε 0h 2
met a0 =
π me e 2
ψ1s bevat informatie over het elektron in de energietoestand E1s
Z=1
ψ1s streeft asymptotisch naar 0
formules: niet te kennen
Probabiliteitsdistributie ψ2
Z=1
ψ21s
probabiliteit om e in de energietoestand
1s in één punt op een afstand r van de
kern van het H-atoom aan te treffen
•ψ21s streeft asymptotisch naar 0
afmetingen atoom niet exact
gedefiniëerd
•ψ21s grootst dicht bij de kern
57
Atoomorbitaal
Z=1
58
ψ21s
1s orbitaal: boloppervlak omsluit 90% van lading e in toestand 1s
59
32%
93%
ψ21s
% lading omsloten door
bolopp. met straal r
ψ21s
orbitaal = gebied in de ruimte waarbinnen de kans om een
elektron aan te treffen 90% is
60
Volume-gewogen of radiale probabiliteitsdichtheid (RPD)
4πr2ψ21s
Z=1
probabiliteit om e in de energietoestand
1s aan te treffen in één punt op een
afstand r van de kern van het H-atoom
totale probabiliteit om e in de
energietoestand 1s aan te treffen op
een bolopp. op afstand r van de kern
van het H-atoom
meest waarschijnlijke afstand r van de kern om e in
energietoestand corresponderend met ψ1s aan te treffen
61
Eén-elektronsysteem
E-niveau’s en quantumgetallen
één-elektronsysteem: E-niveau’s
E ψn = −
Z 2 e 4 me
8
ε o2
2
n h
2
= −2.18 × 10 −18 ×
Z2
n
2
62
n = 1, 2....
•ontaarde AO: AO met zelfde E
•toestanden met n ≠1: aangeslagen
of geëxciteerde toestanden
Z = 1: H-atoom
in één-elektronsystemen hebben alle
atoomorbitalen met een zelfde n dezelfde energie
Excitatie elektron in H-atoom
1 H-kern + 1 elektron op afstand ∞ van elkaar en in rust
E=0
E1S
E2S
H
∆E
H
1s1:
↑
2s1:
1ste
E2p
↑
aangeslagen toestand met E2s1
H 2p1: aangeslagen toestand met E2p1 ≡ E2s1
↑
grondtoestand
E1 = − 2.18 × 10 −18 J ×
2
E2 = − 2.18 × 10
−18
J×
1
12
∆E = E2 − E1 = hν foton
12
22
63
64
één-elektronsysteem: quantumgetallen
in één-elektronsystemen worden alle atoomorbitalen
volledig gekarakteriseerd door 3 quantumgetallen
hoofdquantumgetal n
energie, ruimtelijke uitgestrektheid
van orbitaal
nevenquantumgetal l
vorm van orbitaal
magnetisch
quantumgetal ml
ruimtelijke oriëntering van orbitaal
65
n = 1, 2, 3, ….
l = 0, 1, 2, …n-1
n
l
ml
orbitaalnotatie
1
2
0
0
1
0
0
-1,0,1
1s
2s
2p
3
0
1
2
0
1
2
3
0
-1,0,1
-2,-1,0,1,2
0
-1,0,1
-2,-1,0,1,2
-3,-2,-1,0,1,2,3
3s
3p
3d
4s
4p
4d
4f
4
ml= 0, 1, 2...l
aantal
aantal
orbitalen orbitalen in
in schaal subschaal
1
1
4
1
3
9
16
1
3
5
1
3
5
7
één-elektronsysteem: vorm orbitalen
66
s-orbitaal: l = 0
•1s golffunctie: n = 1, l = 0, ml = 0 ⇔ E1s
ψ1s
 1  Z 
=
  
 π   a0 
3
2
 − Zr 

exp 
 a0 
met a0 =
ε0h2
π me e 2
•2s golffunctie: n = 2, l = 0, ml = 0 ⇔ E2s
ψ 2s
 1  Z 
 
=
 4 2 π   a0 

 
3
2

 − Zr 
Zr 
 2 −
 exp 

a0 

 2 a0 
• ψ1s en ψ2s enkel afhankelijk van r ⇒ sferisch symmetrisch
• alle s golffuncties zijn sferisch symmetrisch
l = 0 ⇒ s orbitaal is bolvormig
formules: niet te kennen
67
ψ1s
 1  Z 
=
  
 π   a0 
3
2
 − Zr 

exp 
 a0 
ψ 2s
 1  Z 
 
=
 4 2π   a 

 0
ψ2s heeft 1 radiale knoop
3
2

 − Zr 
Zr 
 2 −
 exp 

a0 

 2 a0 
ψ2s is meer “uitgespreid” in ruimte dan ψ1s
68
de Broglie staande golf: ψi
λ = 2L
+
n=1
ψ i2
knoop
n=2
+
−
λ=L
golffunctie ψi
ψ i2
+
λ e,1s > λ e,2s
1s
r
kern
2s
+
−
kern
kern
r
knoop
−
r
kern
r
69
RPD
vergelijking
met r1 Bohr
vergelijking
met r2 Bohr
vergelijking
met r3 Bohr
70
p-orbitaal: l = 1
l = 1 ⇒ ml = -1, 0, 1: drie p orbitalen
2p-golffuncties: n = 2, l = 1, ml = -1, 0, +1 ⇔ E2p
3
 1   Z  2  Zr 
 − Zr 


    exp 
 cos θ
ψ 2p z = 

 2 a0 
 4 2 π   a0   a 0 
3
 1   Z  2  Zr 


     exp  − Z r  sin θ cos φ
ψ 2p x = 
 2a 
 a  a 
4
2
π
0
0




 0


ψ2pz = 0 in xy-vlak
ψ2px = 0 in yz-vlak
3
 1   Z  2  Zr 
 − Zr 






 sin θ sin φ
ψ 2p y = 
exp 





 2 a0 
 4 2 π   a0   a 0 
ψ2py = 0 in xz-vlak
•zelfde exponentiële verval als 2s functie ⇒ 2s en 2p orbitalen ≅ grootte
•2p functies zijn enkel 0 voor r = 0 ⇒ hebben geen radiale knoop
formules: niet te kennen
71
ψ22pz
de drie p orbitalen verschillen enkel door hun oriëntatie in de ruimte
72
2s elektron heeft
grotere kans om
zich dichter bij de
kern te bevinden
dan 2p elektron
2s en 2p orbitalen hebben
nagenoeg gelijke grootte
2s heeft 1 radiale knoop
2p heeft 1 knoopvlak en GEEN radiale knoop
73
•3p-orbitalen: n = 3, l = 1, ml = -1, 0, +1 ⇔ E3p
radiale
knoop
ψ2p
ψ3p
radiale knoop
Radiale probabiliteitsdistributie
Radiale probabiliteitsdistributie
knoopvlak
74
3s elektron
heeft grotere
kans om zich
dichter bij de
kern te
bevinden dan
3p elektron
3s en 3p orbitalen
hebben nagenoeg
gelijke grootte
Z=1
3s heeft 2 radiale knopen
3p heeft 1 knoopvlak en 1 radiale knoop
75
d-orbitaal: l = 2
l = 2 ⇒ ml = -2, -1, 0, 1, 2 : vijf d orbitalen
•3d-orbitalen: n = 3, l = 2, ml = -2, -1, 0, +1, +2 ⇔ E3d
knoopvlak
z
knoopoppervlak
x
y
Z=1
76
•4d-orbitalen: n = 4, l = 2, ml = -2, -1, 0, +1, +2 ⇔ E4d
radiale knoop
77
f-orbitaal: l = 3
l = 3 ⇒ ml = -3,-2, -1, 0, 1, 2, 3 : zeven f orbitalen
•4f-orbitalen: n = 4, l = 3, ml = -3, -2, -1, 0, +1, +2, +3 ⇔ E4f
Z=1
Z=1
gemiddelde afstand e tot kern
r nl =
a0 =
2
n a0
Z
ε oh 2
π me e
2
78
1s: n = 1, l = 0
 1  l(l + 1) 

1 + 2 1 −
2
n



= 5.29 × 10 −10 m
2s: n = 2, l = 0
Bohrse straal
2p: n = 2, l = 1
Radiale probabiliteitsdistributie
enkel elektron in s-orbitaal kan
tot dicht bij de kern doordringen
3s: n = 3, l = 0
3p: n = 3, l = 1
3d: n = 3, l = 2
Aftsand r tot de kern [a0]
79
QM-atoommodel:
meer-elektronsysteem
80
•Schrödinger: quantummechanische atoommodel
•meer-elektronsysteem: elektrostatische afstoting elektronen
•vierde quantumgetal: spinquantumgetal ms = +1/2, −1/2
•limiet op aantal elektronen in 1 orbitaal: Pauli principe
•complexere set E-niveaus: E = f(n, l)
•elektronenconfiguratie: aufbau-principe
•valentie-elektronen
•Elektronenconfiguratie en periodiciteit
•periodieke eigenschappen: wat versus waarom
•periodieke eigenschappen: atoomstraal, ionenstraal,
ionisatie-energie, elektronenaffiniteit
Spinquantumgetal: ms = +1/2, −1/2
elk elektron in een atoom wordt volledig gekarakteriseerd
door zijn 4 quantumgetallen (n, l, ml, ms)!!!
Pauli uitsluitingsprincipe
•limiet op aantal elektronen in 1 orbitaal
geen twee elektronen in een zelfde atoom kunnen
dezelfde 4 quantumgetallen hebbben
een atoomorbitaal kan slechts twee elektronen met
tegengestelde spins bevatten
81
Complexere set E-niveaus: E = f(n,l)
elektrostatische effecten ⇒ opsplitsing van E-niveaus
AO in een subniveau (l: s, p, d, f) binnen een gegeven
niveau (n) hebben een verschillende energie
82
E = f(n, l) ⇔ afscherming
83
afstoting
•kern-elektron: Eaantrekking < 0
aantrekking
Ze × ρe (r )
E∝ −
r
valentieelektronen
kern
•elektron-elektron: Eafstoting > 0
ρe (r1) × ρe (r2 )
E∝
r1,2
ρe(r): e-densiteit in punt op
afstand r van de kern
beschrijven alsof e aangetrokken worden door kern met Zeffectief
Zeffectief = Z − effect afstoting = Z – afscherming
En = −
Z 2eff ,n
n
2
n2 a0
r nl =
Z eff ,n
[Rydberg ]
n = 1, 2....
 1  l(l + 1) 

1 + 1 −
2
n

 2
n=1
n=2
84
n=3
1s2 2s2 2p6 3s2 3p6
kern: 18+
Argon
85
afschermingseffecten door elektronen in lagere niveaus
1s2 2s2 2p6 3s2 3p6
Argon
schermen e met n = 3 sterk af
n = 1; Zeff,1 = 16+
n=1
n = 2; Zeff,2 = 13+
n=2
n=3
n = 3; Zeff,3 = 6.5+
+18
2e
8e
8e
schermen e met n = 2 sterk af
ruwe
schatting Zeff 18+
16+
8+
kern: 18+
enkel elektron in s-orbitaal kan tot
dicht bij de kern doordringen
86
•afscherming binnen zelfde niveau
s elektronen schermen p en d elektronen af
p elektronen schermen d elektronen af
•afscherming binnen zelfde subniveau
s elektronen schermen elkaar zwak af
p elektronen schermen elkaar zwak af
d elektronen schermen elkaar zwak af
belang afscherming neemt toe naarmate
d subniveau verder opgevuld wordt
Samenvatting afschermingseffecten
87
e in het hoogst bezette E-niveau worden:
•sterkst afgeschermd door e in de lagere niveaus
•minder sterk afgeschermd door e in hetzelfde niveau (s<p<d<f)
vb.: 4f e worden sterker afgeschermd dan 4p e
•zwak afgeschermd door elektronen in hetzelfde subniveau
vb.: 4p elektronen schermen elkaar slechts zwak af
⇒ energievolgorde van de orbitalen
88
log-schaal
Z↑
↑ ⇒ kernlading ↑
E↓
↓
1 Rydberg = 2.18 × 10-18 J
89
Elektronenconfiguratie meer-e systemen
•Wat?
De verdeling van de elektronen over de beschikbare AO
•Hoe bepalen?
De e-configuratie van de grondtoestand van een atoom wordt
gevonden door toepassen van het aufbau-principe
1. De orbitalen met de laagste energie worden eerst opgevuld
2. Een orbitaal kan slechts twee elektronen met tegengestelde spins
bevatten (Pauli uitsluitingsprincipe)
3. Indien twee of meer orbitalen dezelfde energie hebben
(gedegeneerde orbitalen) dan wordt elk van deze orbitalen half
gevuld; de elektronen in de half gevulde orbitalen hebben allen
hetzelfde spinquantumgetal (Regel van Hund)
90
orbitaaldiagram
orbitaal voorstellen als
cirkel of vierkant en de
elektronen in de
orbitaal voorstellen met
pijl. De richting van de
pijl stelt de spin van het
elektron voor.
91
E
Z
!
transitiemetalen: 4s e minder sterk gebonden aan kern dan 3d e
92
93
l
0
n
1
2
3
4
5
6
1
1s
2
2s
2p
3
3s
3p
3d
4
4s
4p
4d
4f
5
5s
5p
5d
5f
5g
6
6s
6p
6d
6f
6g
6h
7
7s
7p
7d
7f
7g
7h
7i
8
8s
8p
8d
8f
8g
8h
8i
7
8j
Valentie-e: e in hoogst bezette E-niveaus
94
alle elementen uit zelfde (hoofd)groep hebben
dezelfde e-configuratie voor hun valentieschaal
Paramagnetisme en diamagnetisme
•paramagnetisme: atoom/ion/molecule met ongepaarde
elektronen wordt aangetrokken door magneetveld
•diamagnetisme: atoom/ion/molecule met enkel gepaarde
elektronen wordt niet aangetrokken door magneetveld
paramagnetisch
diamagnetisch
95
96
Voorbeeld 4
Schrijf de elektronenconfiguratie en bepaal
de magnetische eigenschappen van:
a) Zn en Zn2+
b) Fe, Fe2+ en Fe3+
97
98
Opgave 3.14
Veronderstel een universum waarin de vier quantumgetallen
dezelfde mogelijke waarden kunnen hebben als in ons
universum met dit verschil dat het nevenquantumgetal als
waarden 0, 1, 2 … (n+1) kan aannemen.
a) Hoeveel elementen zouden er in de eerste twee perioden van
het periodiek systeem van dit universum voorkomen?
b) Wat zou het atoomgetal zijn van het element in de tweede
periode en de vijfde kolom?
c) Teken een orbitaaldiagramma voor het element met
atoomgetal 12
99
100
101
Periodieke
eigenschappen
102
e-configuratie en
periodiciteit
periodieke eigenschap = periodieke functie van atoomgetal103
104
Periodieke eigenschappen: wat versus waarom
•Mendeleev: periodieke wet (maakt voorspellen mogelijk)
Q
R
S
Q’
R’
S’
Q”
R”
S”
eigenschap van R’ kan bepaald als gemiddelde
van de eigenschappen van R, R”, Q’ en S’
1
AMR ' = (AMR + AMR " + AMQ' + AMS' )
4
AMAs =
1
(AMP + AMSb + AMGe + AMSe )
4
AMAs =
1
(31 + 122 + 73 + 79 ) = 76
4
AMAs = 76 ⇔ PS : AMAs = 74.92
•QM-atoommodel: e-configuratie (maakt verklaring
mogelijk)
alle elementen uit zelfde groep hebben dezelfde e-configuratie voor
hun valentieschaal ⇒ analoge fysische en chemische
eigenschappen
•periodieke eigenschappen
•atoomstraal
•ionenstraal
•ionisatie-energie (IE)
A(g) → A+(g) + e-
∆E = IE
•elektronen-affiniteit (EA)
A(g) + e- → A-(g)
∆E = EA
105
106
Trends periodieke eigenschappen
107
Periodiciteit atoomstraal
108
Periodieke eigenschap: atoomstraal
•binnen groep: atoomstraal↑ met Z↑
vb.: Li → Fr
•binnen periode: atoomstraal↓ met Z↑
vb.: Na → Cl
109
Verklaring periodieke trends atoomstraal
ratoom = f(Z): wordt bepaald door twee
tegengestelde invloeden
•verandering in n
• n↑ ⇒ ruimtelijke uitgestrektheid orbitaal ↑
⇒ atoomstraal ↑
•verandering in Zeff
• Zeff↑ ⇒ aantrekking tussen e en kern ↑
⇒ atoomstraal ↓
110
•binnen groep: atoomstraal↑ met Z↑
→
Li
e-configuratie: Li: [He]2s1
Fr
Fr: [Rn]7s1
n=1 n=2 n=3 n=4 n=5 n=6 n=7
Li: Z = +3
2e
↑
Fr: Z = +87
2e
8e
Ruwe schatting Zeff:
Zeff ≈ 3 – 2 = 1
8e
18e
18e
32e
↑
Zeff ≈ 87 – 86 = 1
86e
•Zeff valentie-elektronen verandert weinig
•n valentie-elektronen↑ ⇒ ruimtelijke uitgestrektheid orbitaal ↑
⇒ atoomstraal ↑
•binnen periode: atoomstraal↓ met Z↑
→
Na
e-configuratie: Na: [Ne]3s1
n=1 n=2
Ar
Ar: [Ne]3s23p6
Ruwe schatting Zeff:
3s 3p
Na: Z = +11
2e
8e
↑
Ar: Z = +18
2e
8e
↑↓
111
Zeff ≈ 11 – 10 = 1
↑↓
↑↓
↑↓
Zeff ≈ 18 – 10 = 8
10e
•Zeff valentie-elektronen↑ ⇒ aantrekking valentie-e en kern ↑
•n valentie-e blijft gelijk
⇒ atoomstraal ↓
Atoomstraal transitiemetalen
112
vanaf 4 t.e.m. 8 d elektronen blijft r ongeveer gelijk
Atoomstraal transitiemetalen
113
Z↑⇒r↓
Zeff ↑
afscherming d elektronen wint
aan belang
> 5 d-elektronen
vanaf 4 t.e.m. 8 d elektronen blijft r ongeveer gelijk
opvulling 4f-orbitalen
lanthanidecontractie
114
Opgave 3.35
Rangschik de volgende atomen in volgorde
van toenemende grootte:
a) Be, Mg, Ca
b) Te, I, Xe
c) Ga, Ge, In
d) As, N, F
e) S, Cl, F
a) Be < Mg < Ca
b) Xe < I < Te
c) Ge < Ga < In
d) F < N < As
e) F < Cl < S
115
116
Periodiciteit ionisatieenergie (IE)
Definitie ionisatie-energie (IE)
gasfase
A(g) → A+(g) + e-
117
∆E = IE
E = 0; kern + elektronen op afstand ∞ en in rust
IEA
↑
↑↓
↑↓
↑↓
↑↓
↑↓
AO van A in
grondtoestand
EA+
EA
A+(g)
IEA
ion in grondtoestand en e
op afstand ∞ en in rust
A
atoom in grondtoestand (g)
IE> 0: er moet steeds E toegevoerd worden om e uit aantrekkingsveld van
kern te verwijderen
IEatoom = energie nodig om e uit hoogst bezette AO te verwijderen
Periodiciteit IE
118
Verklaring periodieke trends IE
119
•alkalimetalen hebben de laagste IEs
ruwe schatting Zeff alkalimetalen: +1
zwakke aantrekking tussen te verwijderen e en kern ⇒ lage IE
•edelgassen hebben de hoogste IEs
ruwe schatting Zeff edelgassen: +8
sterke aantrekking tussen te verwijderen e en kern ⇒ hoge IE
120
•binnen groep: IE↓ met Z↑
n↑ ⇒ ruimtelijke uitgestrektheid orbitaal ↑
Zeff valentie e verandert weinig
⇒ aantrekking tussen e en kern ↓
⇒ IE↓
•binnen periode: IE↑ met Z↑
n = ⇒ aantal binnenste schalen =
afscherming valentie e verandert weinig ⇒ Zeff↑
⇒ aantrekking tussen e en kern↑
⇒ IE↑
121
Onregelmatigheden binnen periode
!
Be: 2s2
B: 2s2 2p1
Be+: 2s1
B+: 2s2
IE = 899.4 kJ/mol
IE = 800.6 kJ/mol
⇒ IE 2s > IE 2p
⇒ e in 2s minder afgeschermd dan e in 2p
⇒ e in 2s ondervindt grotere Zeff dan e in 2p
⇒ e in 2s sterker gebonden aan kern dan e in 2p
122
Hogere IEs
A(g) + IE1→ A+(g) + eA+(g) + IE2→ A2+(g) + eA2+(g) + IE3→ A3+(g) + ekJ/mol
IE3 > IE2 > IE1
123
Opgave 3.21
Welk van de volgende atomen heeft de
hoogste 1ste IE?
a) P
b) N
c) Sb
d) As
124
125
Periodiciteit
elektronenaffiniteit (EA)
Definitie elektronenaffiniteit (EA)
gasfase
A(g) + e- → A-(g)
∆E = EA
E = 0; kern + elektronen op afstand ∞ en in rust
EAA
↑
↑↓
↑↓
↑↓
↑↓
↑↓
AO van A in
grondtoestand
EA−
EA
A
atoom in grondtoestand en(g)
e op afstand ∞ en in rust
EAA
A−(g)
anion in grondtoestand
EA is meestal < 0: er wordt meestal E vrijgesteld wanneer e in
aantrekkingsveld van kern komt
EA = E die vrijkomt bij toevoegen van e in laagste niet-bezette AO
EA = maat stabiliteit anion; EA meer negatief ⇒ anion stabieler
EA > 0 ⇒ anion onstabiel
126
Periodiciteit EA
•halogenen: meest negatieve EA
•edelgassen: positieve EA
127
A(g) + e- → A-(g)
∆E = EA (kJ/mol)
•halogenen: meest negatieve EA ⇒ grootste neiging om e op te nemen
⇒ men zegt: edelgassen hebben de grootste elektronenaffiniteit
•edelgassen: positieve EA ⇒ kleinste neiging om e op te nemen
⇒ men zegt: edelgassen hebben de kleinste elektronenaffiniteit
128
Verklaring periodieke trends EA
EA = f(Z): wordt bepaald door twee
tegengestelde invloeden
•aantrekking bijkomend e-kern
energetisch gunstig ⇒ negatieve EA
⇒ stabiel anion
•repulsie bijkomend e-e
energetisch ongunstig ⇒ positieve EA
⇒ onstabiel anion
129
130
•edelgassen: positieve EA
bijkomend (n+1)s e sterk afgeschermd door (n) e ⇒ lage Zeff.
zwakke aantrekking tussen bijkomend e en kern
energetisch ongunstig ⇒ EA > 0
•halogenen: meest negatieve EA
bijkomend (n)p e zwak afgeschermd door (n) e ⇒ hoge Zeff
sterke aantrekking tussen bijkomend e en kern
energetisch gunstig ⇒ EA << 0
Hogere EAs
E = 0: O-kern + 10 e op afstand ∞ en in rust
O2−(g)
+737 kJ
EA2 = +878 kJ
O(g) + 2 e
EA1 = −141 kJ
O−(g) + e
O(g) + e → O−(g)
∆E = EA1 = –141 kJ/mol
O−(g) + e → O2−(g)
∆E = EA2 = +878 kJ/mol
O(g) + 2 e → O2−(g)
∆E = EA1 + EA2 = +737 kJ/mol
131
132
edelgassen hebben een hoge IE én een positieve EA ⇒ weinig reactief
Metalen hebben een lage ionisatie-energie; vormen kationen
Niet-metalen hebben een hoge elektronen-affiniteit; vormen anionen
grote negatieve EA
133
Opgave 3.20
Welk van onderstaande elementen heeft
de meest negatieve EA?
a) Cl
b) Na
c) I
d) Se
e)Ar
Cl heeft grootste elektronenaffiniteit
134
135
Opgave 3.27
Verklaar waarom IE1 van Ca groter is dan
IE1 van K terwijl nochtans IE2 van Ca
kleiner is dan IE2 van K.
Zeff Ca > Zeff K ⇒ IE1 Ca > IE1 K
Zeff Ca+ <<< Zeff K+⇒ IE2 Ca < IE2 K
136
137
Periodiciteit ionenstraal
138
Periodieke eigenschap: ionenstraal
•kationen
•straal kation < straal atoom
•↓ groep ⇒ straal kation↑
2
3
4
5
6
•anionen
•straal anion > straal atoom
•↓ groep ⇒ straal anion↑
verklaring kationstraal < atoomstraal
11 elektronen
10 elektronen
12 elektronen
Z = 11
[Ne] 3s1
n=3
p+
139
Z = 11
[Ne]
n=2
+
11
11
+ p
Na : − =
= 1 versus Na : − =
= 1 .1
11
10
e
e
Z = 12
[Ne] 3s2
n=3
10 elektronen
Z = 12
[Ne]
n=2
p+
+
12
12
2+ p
Mg : − =
= 1 versus Mg : − =
= 1 .2
12
10
e
e
gemiddelde aantrekkingskracht van kern op elektronen
is groter in kation dan in neutraal atoom ⇒ rkation < ratoom
140
verklaring trends iso-elektronische atomen/ionen
iso-elektronisch: zelfde e-configuratie ⇒ e-e repulsies zijn gelijk
Z = 10
[Ne]
n=2
p+
10
Ne : − =
=1
10
e
Z = 11
[Ne]
n=2
p+
11
Na + : − =
= 1.1
10
e
Z = 12
[Ne]
n=2
Mg2 + :
p+
e−
=
12
= 1.2
10
iso-elektronisch atoom/ion: Z↑ ⇒ r↓
Zie ook figuur 3.42
141
2
∆r = 34 pm
∆r = 40 pm
3
∆r = 33 pm
∆r = 39 pm
4
∆r = 14 pm
∆r = 10 pm
5
6
162
n=4
opvulling 3d-orbitalen; transitiemetalen: ratoom↓ met Z↑ tot 4 d-elektronen;
ratoom↑ lichtjes voor meer dan 8 d-elektronen; 4-8 d-elektronen: ratoom ≅
142
170
1.30
150
1.25
1.20
110
90
1.15
70
1.10
50
1.05
30
10
1.00
Sc
Ti
V
atoom
Cr Mn Fe Co Ni Cu Zn
2+ ion
trend
p+/e-
p+/e-
straal (pm)
130
143
Studie-opgave 3.19
Duid voor elk van onderstaande paren het
atoom of ion aan met de grootste straal:
a) Na en K
b) Cs en Cs+
c) Rb+ en Kr
d) K en Ca
e) Cl− en Ar
144
145
Studie-opgave 3.20
Duid voor elk van de onderstaande paren
het ion aan met de grootste straal:
a) O− en S2−
b) Co2+ en Ti2+
c) Mn2+ en Mn4+
d) Ca2+ en Sr2+
146
147
Examenstof
belangrijke vaardigheden
•interconversie frequentie, golflengte, energie elektromagnetische straling
•berekening frequentie van geëmitteerde fotonen door geëxciteerde atomen
•berekening frequentie van geabsorbeerde fotonen bij excitatie atomen
•set quantumgetallen ⇔ orbitaal
•tekenen en benoemen van orbitalen
•schrijven/voorspellen elektronenconfiguratie van atomen in de grondtoestand
•orbitaalvoorstelling van elektronenconfiguratie
•elektronenconfiguratie valentie-schaal voor groepen in PS
•identificatie van blok in PS waartoe een element behoort
•bepalen/verklaren relatieve grootte van de atoomstralen voor een set atomen
•bepalen/verklaren relatieve grootte van de stralen voor een set ionen
•bepalen/verklaren relatieve grootte van IE’s voor een set atomen
•bepalen/verklaren relatieve grootte van EA’s voor een set atomen