Golfvergelijking van Schrodinger

De golfvergelijking van Schrödinger
De golfvergelijking van Schrödinger beschrijft het gedrag van het elektron in het atoom.
De oplossing van die vergelijking ? i bevat informatie over de energie in de toestand i.
? i wordt gekarakteriseerd door:
•
•
kwantumgetallen
energie Ei in de toestand i.
? 2i is de waarschijnlijkheid om een elektron aan te treffen in een gebied van de ruimte.
Zo is bijvoorbeeld ψ2 1s is de waarschijnlijkheid om een elektron aan te treffen op een afstand r
van de kern voor het elektron op de baan 1s.
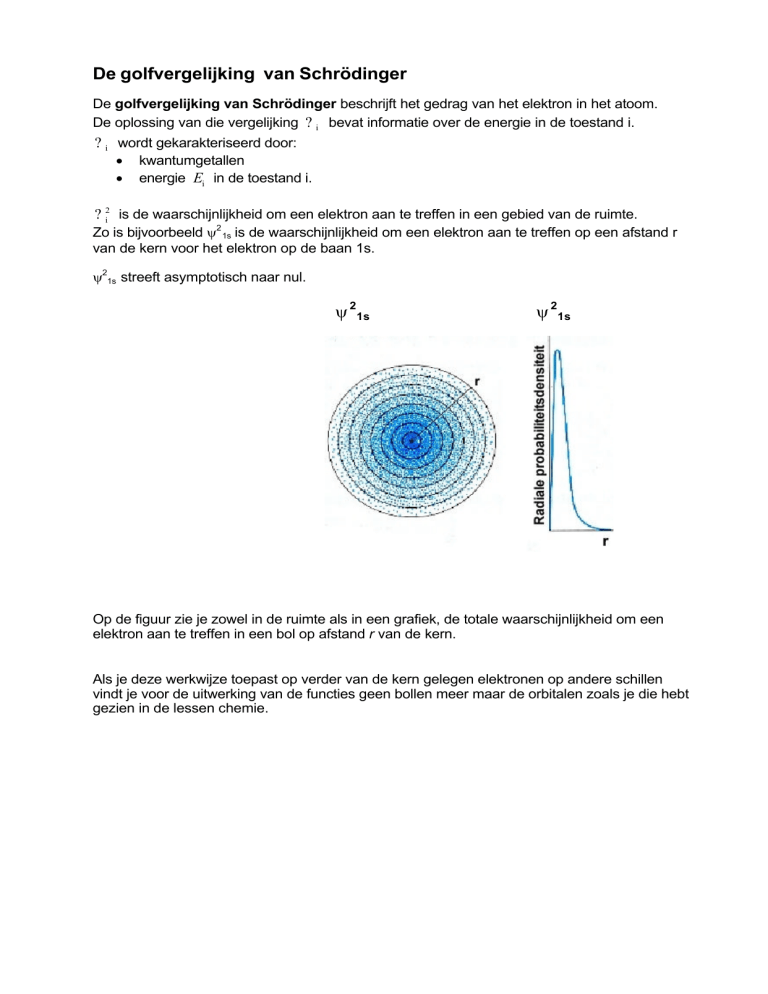
ψ21s streeft asymptotisch naar nul.
ψ 21s
ψ 21s
Op de figuur zie je zowel in de ruimte als in een grafiek, de totale waarschijnlijkheid om een
elektron aan te treffen in een bol op afstand r van de kern.
Als je deze werkwijze toepast op verder van de kern gelegen elektronen op andere schillen
vindt je voor de uitwerking van de functies geen bollen meer maar de orbitalen zoals je die hebt
gezien in de lessen chemie.
Op deze figuur hiernaast zie je de waarschijnlijkheden
om het elektron aan te treffen op een bepaalde afstand
van de kern.
De pieken van de grootste waarschijnlijkheid voor de
verschillende elektronen komen nagenoeg overeen
met de stralen die Bohr berekend had.
Je kan echter de ruimtelijke weergave van de orbitalen verkiezen. Hieronder volgen enkele
voorbeelden van p-orbitalen waarbij in de golfvergelijking de energiewaarden voor de pelektronen werden ingevuld. De lussen zijn plaatsen waar de waarschijnlijkheid om het elektron
aan te treffen het grootst is.
Kwantumgetallen
In een wordt atoom elk elektron gekarakteriseerd door vier kwantumgetallen:
•
•
•
•
hoofdkwantumgetal n: bepaalt de energie en de ruimtelijke uitgestrektheid van de
orbitaal
nevenkwantum getal l : bepaalt de vorm van het orbitaal
magnetisch kwantumgetal m : bepaalt de ruimtelijke ordening van de orbitaal
spin kwantumgetal s : bepaalt de spin van het elektron (+1/2 of –1/2)
Een elektron in een atoom wordt volledig gekarakteriseerd door zijn vier kwantumgetallen.
Later voegde Pauli hier nog zijn uitsluitingsprincipe aan toe:
• in een atoom kunnen geen twee elektronen dezelfde vier kwantumgetallen hebben
• op een orbitaal kunnen slechts twee elektronen met tegengestelde spin voorkomen
Kwantummechanica
Op 14 december 1900 presenteerde Max Planck aan de Duitse Natuurkundige Kring een paper
waarin hij voorstelde dat energie enkel kan worden ontvangen en verzonden in afzonderlijke
pakketjes, die hij kwanta noemde. Het duurde enkele jaren voor de reikwijdte van die stelling
doordrong, maar nu wordt dit algemeen aanzien als het moment waarop de kwantummechanica
werd geboren.
Kwantummechanica is de tak van de natuurkunde die het gedrag van materie en licht op
atomaire en subatomaire schaal bestudeert.
Kwantummechanica gaat in tegen het gezonde verstand, tegen de manier waarop we de
alledaagse wereld ervaren en begrijpen. In de kwantumwereld zijn oorzaak en gevolg niet
noodzakelijk met elkaar verbonden, kunnen subatomaire deeltjes zich op twee plaatsen tegelijk
bevinden tot iemand het meet en kan licht zowel een golf als een deeltje zijn.
Planck was net als andere natuurkundigen in die tijd, enkel op zoek naar een beschrijving van
de manier waarop de kleur (de spectrale kenmerken) van warmtestraling samenhangt met de
temperatuur van het object.
Op dat moment werd algemeen aanvaard dat licht zich gedraagt als een golf, een wereld die
streng gescheiden was van de manier waarop deeltjes zich gedragen. Planck kwam met een
vergelijking op de proppen die mooi klopte met de resultaten van experimenten, maar kon
aanvankelijk niet verklaren waarom deze vergelijking de juiste was. Op 14 december 1900
stelde hij toch een uitleg voor, maar noemde die zelf een ‘wanhoopspoging’. De oplossing
bestond erin te aanvaarden dat atomen energie in aparte pakketjes, door Planck kwanta
genoemd, uitstralen en niet in de continue golven die de elektromagnetische theorie
veronderstelt. Een revolutionaire gedachte, maar Planck, die zichzelf altijd als een brave en
oplettende burger beschouwde, bekeek het als een theoretische constructie die geen uitstaans
had met wat er in werkelijkheid gebeurde.
In 1905 zag een jonge klerk in een patentenbureau, Albert Einstein, meer in de hypothese van
Planck. Hij ontdekte dat ook het foto-elektrisch effect - de uitstoot van elektronen wanneer een
metalen oppervlak beschenen wordt met licht of x-stralen - verklaard kon worden door licht te
beschouwen als een verzameling kleine energiebundeltjes: fotonen.
Ook in 1905 ontdekte Rutherford de atomaire kern, een idee dat in 1913 door Niels Bohr
verder werd uitgewerkt. Hij stelde voor een atoom als een miniatuurzonnestelsel te
beschouwen, waarbij elektronen als planeten om de atoomkern cirkelden. Elektronen kunnen
daarbij niet eender welke omloop volgen, maar krijgen slechts de keuze tussen enkele banen.
Meteen was verklaard waarom een atoom niet instort: de laagste omloop is nog steeds een
eindje van de kern verwijderd. Het verklaart ook waarom verschillende elementen straling
uitzenden in specifieke golflengten. Deze corresponderen met de energie die wordt vrijgegeven
of geabsorbeerd als een elektron naar een andere baan springt. Vanaf de jaren ‘20 gaat de
kennis over de wereld van het allerkleinste met sprongen vooruit en worden zelfs twee
verschillende kwantumtheorieën opgesteld:
Werner Heisenberg, Max Born en Pascual Jordan stelden een complete kwantumtheorie op,
gebaseerd op Heisenbergs overtuiging dat de fysica gebaseerd moet worden op wat kan
worden gezien en/of gemeten. In 1927 kwam Heisenberg dan met het befaamde
onzekerheidsprincipe voor de dag, dat stelt dat het onmogelijk is zowel de positie als de
snelheid van een deeltje te meten. Een van beiden kan wel, beiden tegelijk echter niet. Omdat
de daad van meten zelf het systeem verstoort, kan hoogstens gemeten worden wat de staat
van het systeem is na deze interactie.
Maar er stond een andere interpretatie aan te komen, die zijn oorsprong vindt bij de Franse
aristocraat Louis de Broglie. Hij stelde zich in zijn doctoraatsthesis de vraag of deeltjes zich
niet als een golf konden gedragen. Dat werd later experimenteel bevestigd.
Het werk van de Broglie inspireerde Erwin Schrödinger, die het elektron niet als een punt
bekijkt, maar als een golffunctie, een wiskundige entiteit die door Born werd verklaard als de
kans om een elektron op een bepaalde plaats te vinden. Daarmee veroverden noties als kans
en waarschijnlijkheid in plaats van voorspelbaarheid en zekerheid - definitief een plaatsje in de
natuurkunde. In 1928 verbond Paul Dirac de bijzondere relativiteitstheorie van Einstein met de
kwantummechanica, voorspelde en passant het bestaan van antimaterie en stond aan de basis
van de ontwikkeling van een nieuwe interpretatie van de kwantumtheorie, de kwantum
veldtheorie, die vandaag in de deeltjesfysica algemeen gebruikt wordt.
Inmiddels is de kwantummechanica overal. Het heeft de logica achter het Periodiek Systeem
van Mendeljev blootgelegd, heeft geholpen de nucleaire processen in de zon bloot te leggen,
vindt zijn toepassing in cd-spelers enzovoort. Het heeft de basis van de klassieke natuurkunde
grondig gesloopt en is een wetenschappelijke revolutie geweest die de aanblik van de wereld
voorgoed veranderde.
De eigenaardige conclusies waartoe de kwantummechanica hebben geleid, kunnen niet
iedereen bevredigen. Einstein erkende de grote waarde ervan, maar zei ook dat “de theorie ons
niet dichter bij het geheim van ‘De Oude’ brengt. Hij (God) speelt niet met dobbelstenen”.
Kwantummechanica wordt nu gebruikt om alle natuurlijke fenomenen te verklaren, op de
zwaartekracht na.
Men is nu op zoek naar de grote geünificeerde theorie, die zwaartekracht en kwantumtheorie
met elkaar moet verzoenen. De kandidaat die daarbij nu het meeste aandacht krijgt is de
supersnaartheorie, waarbij de werkelijkheid wordt gezien als bestaande uit kleine snaren, die
vibreren in een 11-dimensionele ruimte. Maar eigenlijk weet men nog altijd niet wat een elektron
nu precies is. Het is wel een theorie die uitstekend blijkt te werken, ook al gaat zij het rationele
begripsvermogen te boven.