Uitwerking Herhalingsopgaven Mechanica Natuurkunde 1,2

Uitwerking Herhalingsopgaven Mechanica Natuurkunde 1,2
Herzien sept 2006-09-18
Opgave 1
Eerste wet: Als er op een lichaam geen resulterende kracht werkt, verandert de bewging niet.
De grootte en richting van de snelheid is dan constant. (traagheidswet)
Tweede wet: F = m*a
Actie = - reactie: twee lichamen oefenen op elkaal altijd even grote en tegengesteld gericht
krachten uit.
Opgave 2
Door de boot naar achteren te trappen krijg je van de boot een even grote naar voren gerichte
kracht, die de op de wal brengt.
Opgave 3
a) Op de vaas werkt omlaag de zwaardetkracht: Fz = m*g  Fz = 8,0*9,8 = 78 (N)
Omhoog werkt de normaalkracht. Omdat de som van de krachten in y-richting 0 moet zijn
is Fn = Fz = 78 (N)
b) Op de tafel werken 3 krachten: omlaag de zwaartekracht van de tafel en de gewichtskracht
van de vaas, omhoog de normaalkracht.
Gewichtskracht van de vaas = - Fn op de vaas = 78 (N) omlaag. Fx,tafel = m*g = 15*9,8 =
1,5.102 (N). Omdat de som van de krachten in y-richting 0 moet zijn is Fn = Fz + FG,vaas =
147 + 78 (N) = 2,3.102 (N)
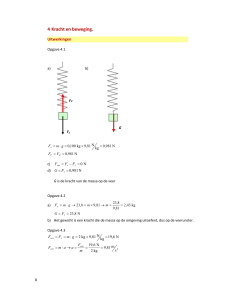
Opgave 4
Zie de tekening hiernaast:
a) Fz,x – Fw = 0, want de snelheid is constant
m*g*sinα – 2,0 = 0  2,5*9,8*sinα = 2,0
Sinα = 0,0816  α = 4,7 o
b) Fn = Fz,y = m*g* cosα = 2,5*9,8*cos4,7 = 24,4
(N) = 24 (N)
c) Fz,x – Fw = m*a  2,5*9,8*sin20o – 2,0 = 2,5 *
a  a = 2,6 (m/s2)
Fz,x
Fw
α
α
Fz,y
Fz
Opgave 5
a) Fres = m*a  Fm – Fw,auto –Fw,caravan = mtot* a  1,65.103 -450 – 700 = (1200 +800)*a
a = 500/2000 = 0,25 (m/s2)
b) Nu alleen naar de krachten op de caravan kijken: Fs – Fw,caravan = mcaravan * a  Fs – 700
= 800*0,25  Fs = 900 (N) = 9,0.102 (N)
Opgave 6
Fz,A = 0,325*9,81 = 3,19 (N)
Fz,B = 0,320*9,81 = 2,94 (N)
a) Kijk naar A en B als één geheel: Fz,A - Fz,B = mtot*a  3,19 – 2,94 = 0,625*a  a = 0,40
(m/s2)
b) Kijk nu naar de krachten op A: Fz,A – Fs = mA*a  3,19 – Fs = 0,325 * 0,40  Fs = 3,1
(N)
c) y(t) = y(0) +v(0).t + ½ * a * t2  1,60 = 0 + 0 + ½*0,40*t2  t = 2,83 (s)
v(t) = v(0) + a*t  v(2,83) = 0 + 0,40 * 2,83 = 1,13 (m/s)
Opgave 7
a) x(t) = x(0) +v(0).t + ½ * a * t2 160 = 0 + 0 +
½* a* 20,02  a = 0,800 (m/s2)
b) Zie de fig hiernaast
sinα = 0,00400  α = 2,29o
Fz = 800*9,81 = 7,85.103 (N)
Fz,x = Fz * sinα = 7,85.103 *0,0400 = 314 (N)
Fmotor
Fz,x
α
Fw
α
Fz,y
Fz
Fmotor – Fz,x – Fw = m*a  Fmotor - 314 – 90 =
800*0,800
Fmotor = 1,04.103 (N) = 1,04 (kN)
Opgave 8
a) Fn = Fz,yB = m*g* cos α = 5,10*9,81*cos8,80o = 49,4 (N)
b) Fz,A = mA*g = 1,70*9,81 = 16,7 (N)
c) Fz,xB = mB*g* sinα = 5,10*9,81*sin8,80o = 7,65 (N). A zal omlaag bewegen en B gaat
langs de helling omhoog. Fz,A – Fz,xB = mtot * a  16,7 – 7,7 = (5,10+1,70)*a  a = 1,33
(m/s2)
d) Kijk naar blok A: FzA – Fs = mA*a  16,7 – Fs = 1,70 * 1,33  Fs = 14,4 (N)
Opgave 9
a) Regel 1: de tijd wordt elke keer 0,01 (s) groter
Regel 2: nieuwe plaats wordt berekend uit ∆x = v*∆t
Regel 3: berekening van de wrijvingskracht uit de snelheid
Regel 4: berekening van de versnelling uit F = m*a
Regel 5: berekening van de nieuwe snelheid met ∆v = a*∆t
b) Tijdens de hele beweging is a
v
negatief, dus de snelheid daalt, de
beweging is vertraagd
c) Zie de fig hiernaast.
d) Nu wordt regel 3: F:=Fmotor –
k*v*v
Bij de startwaarden: Fmotor =
1000
t
B Kracht en impuls
Opgave 10
a) Impuls = massa * snelheid
b) Stoot = kracht*de tijd dat de kracht werkt
c) N*s = kg*m/s2*s = kg*m/s
d) S = m*vna –m*vvoor = m*(vna – vvoor ) = m*∆v, dus 0,72*2,5 = 0,45*∆v ∆v = 4,0 (m/s)
Opgave 11
vvoor = 27,8 (m/s) vna = 0 F = - 6,8.103 (N)
a) Dus: S = m*vna –m*vvoor = m*(vna – vvoor )  - 6,8.103 * ∆t = 1080 * (0 - 27,8)  ∆t = 4,4
(s)
b) Remweg berekenen kan met een energiewet: Ek = Q = Frem * s  ½*1080*27,82 =
6,8.103 * s  s = 61 (m)
Opgave 12
a) Ook hier wordt alle Ek in warmte omgezet: ½*m*v2 = Frem * s  ½*1200*152 = Frem *
0,75  Frem = 1,8.105 (N)
b) S = F* ∆t = m(vna – vvoor)  - 1,8.105 * ∆t = 1200 (0 – 15)  ∆t = 0,10 (s)
Opgave 13
a) Σm*vvoor = Σm*vna (impulsbehoud) Neem de positieve richting naar rechts. Invullen
levert:
(60,0 + 15,0)* - 1,50 = (59,2 + 15,0) * vwagen + 0,80 * - 10,0  - 112,5 = 74,2*vwagen –
8,0 vwagen = - 1,41 (m/s)
b) Σm*vvoor = Σm*vna  74,2 * - 1,41 = 59,2*2,00 + 15,0 * vwagen  - 104,5 = 118,4 + 15,0
* vwagen  vwagen = - 14,9 (m/s)
Opgave 14
a) Hoogteverschil h    . cos 35o = 1,49 – 1,49*cos 35o =
0,27 (m)
b) ½*m*v2 = m*g*h  ½*v2 = 9,81*0,27  v = 2,3 (m/s)
c) Impulsbehoud
mk*vk = (mk+mz)*vz  4,1.10-3 * vk = (4,1+108).10-3*2,3
 vk = 63 (m/s)
d) Q = Ek,voor – Ek,na = ½*4,1.10-3*632 – ½*112,1.10-3*2,32 =
7,8 (J)
35o
C Horizontale worp en cirkelbeweging
Opgave 15
216 (km/h) = 60,0 (m/s)
a) y(t) = ½*g*t2  1200 = ½*9,81*t2  t = 15,64 (s)
x(t) = v*t = 60 * 15,64 = 938 (m)
b) vy = g*t = 9,81*15,64 = 153 (m/s); vx = v = 60,0 (m/s)
Pythagoras: vgrond = √(60,02 + 1532) = 165 (m/s)
tan α = 153/60,0 = 2,56  α = 68,6o een hoek van 68,6o met de grond
Opgave 16
y(t) = ½*g*t2  1,80 = ½*9,81*t2  t = 0,606 (s)
x(t) = v*t = v * 0,606 = 14,00 (m)  v = 23,1 (m/s)
Opgave 17
a) vy = √(v2 – vx2) = √(112 – 102) = 4,58
(m/s)
vy = g*t  4,58 = 1,6*t  t = 2,9 (s)
b) y(t) = ½ *g*t2 = ½*1,6*2,92 = 6,6 (m)
c) x(t) =vbegin*t = 10*2,9 = 29 (m)
vx = 10 (m/s)
vy
v = 11 (m/s)
Opgave 18
2 * * r
2 *  *1,5.1011

 3,0.10 4 (m / s)  30(km / s)
a) vbaan 
T
365,25 * 24 * 60 * 60
2 *
2 *

 2,0.10 7 (rad / s)
T
365,25 * 24 * 60 * 60
 (t )   * t  2,0.10 7 * 30 * 24 * 3600  0,52(rad )
b)  
c)
Opgave 19
a) V = 0,0500 (m/s). lengte = v*t = 0,0500*45*60 = 135 (m)
b) Laagste hoeksnelheid als r het grootst is, dus r = 0,024 (m) v = ω*r 0,0500 = ω*0,024
 ω = 2,08 (rad/s)
Hoogste hoeksnelheid als r het kleinst is, dus r = 0,011 (m) v = ω*r 0,0500 = ω*0,011
 ω = 4,55 (rad/s)
c) Laagste toerental. In 60 (s) is de afgelegde hoek 2,08*60 = 125 (rad) dit zijn 125/(2*π) =
20 omwentelingen per (s)
Hoogste toerental. In 60 (s) is de afgelegde hoek 4,55*60 = 273 (rad) dit zijn 273/(2*π) =
43 omwentelingen per (s)
D Middelpuntzoekende kracht
Opgave 20
90 (km/h) = 25 (m/s)
a) Fw,zijwaarts levert de benodigde middelpuntzoekende kracht dus Fw,zijw. = Fmpz = m*v2/r =
1200*252/200 = 3750 (N) = 3,8 (kN).
b) Als v maximaal is in de bocht is de Fw,zijw. maximaal, dus 6,0.103 (N)
6,0.103 = 1200*v2/200  v = 32 (m/s) (= 114 (km/h))
c) Als de snelheid hoger is is er niet voldoende kracht om de benodigde middelpuntzoekende
kracht te leveren, de straal van de bocht wordt dan groter dan 200 (m) en de auto komt
naast de weg terecht.
Opgave 21
Fz = 1,20*9,81 = 11,8 (N)
a) In het hoogste punt werken Fn en Fz beide naar beneden.  Fn + Fz = Fmpz
Fn + Fz = m*ω2*r  Fn + 11,8 = 1,2*3,02*1,4  Fn = 3,3 (N)
In het laagste punt werkt Fn omhoog en Fz naar beneden.  Fn - Fz = Fmpz
b) Fn - Fz = m*ω2*r  Fn - 11,8 = 1,2*3,02*1,4  Fn = 27 (N)
Als de hoeksnelheid minimaal is, is in het hoogste punt de normaalkracht 0. Dus daar
geldt: Fz = Fmpz  11,8 = 1,20*ω2*1,4  ω = 2,65 (rad/s) = 2,7 (rad/s)
Opgave 22
a) Omdat er geen wrijving is, moet haar startpunt links even hoog zijn als B. Zie ook
uitwerking van opgave 14 a)
Hoogteverschil h    . cos α  3,5 = 6,0 – 6,0*cos α  α = 65o
b) Omzetting Ez in Ek  m*g*h = ½*m*v2  9,81*3,5 = ½ v2  v = 8,3 (m/s)
c) In A: Fs – Fz leveren Fmpz dus: Fs - 50*9,8 = 50*8,32/6,0  Fs = 1063 (N) = 1,1 (kN)
d) ampz = v2/r = 8,32/6,0 = 11 (m/s2)
Opgave 23
a) Bij de kegelslinger geldt: sinα = 0,30/0,90 = 0,33  α = 19o
b) Fs,y = Fz = m*g = 70.10-3* 9,81 = 0,69
(N)
Fs,y = Fs * cos α  0,69 = Fs * cos 19o
 Fs = 0,73 (N)
c) Fs,x = Fs * sin α = 0,73*sin19o = 0,2364
(N)
Fs,x levert Fmpz , dus: 0,2364 =
0,070*v2/0,30
 v = 1,0 (m/s)
d) In één minuut wordt 60*1,0 = 60 (m)
afgelegd. Dat zijn 60/(2*π*0,30) = 32
minuut.
Fs
α
Fs,y
0,90 (m)
α
α
M
r = 0,30 (m)
Fs,x
omwentelingen per
Fz
Opgave 24
a) Omzetting Ez in Ek  m*g*h = ½*m*v2  9,81*0,40 = ½ vB 2  vB = 2,8 (m/s)
m*g*hA = ½*m*vC 2+ m * g * hC  9,8 * 0,40 = ½ vC2 + 9,8 * 0,20  vC = 2,0 (m/s)
b) In B: Fn – Fz = Fmpz = m*v2/r (in B is de beweging een cirkelbeweging Fn = Fz is beslist
fout!!) Invullen levert: Fn – 0,010*9,8 = 0,010*2,82/0,10  Fn = 0,88 (N)
In C: Fn + Fz = Fmpz = m*v2/r Invullen levert: Fn + 0,010*9,8 = 0,010*2,02/0,10  Fn =
0,29 (N)
c) Het stuk CD is een paraboolbeweging, een horizontale worp:
y(t) = ½*g*t2  0,40 = ½*9,8*t2  t = 0,286 (s)
x(t) = v*t = 2,0 * 0,286 = 0,57 (m)
d) Omdat er nergens wrijving is, moet in D de kinetische energie precies even groot zijn als
in B (in beide punten is Ez gelijk) Dus vD = vB = 2,8 (m/s)
E Gravitatie en satellieten
Opgave 25
Fgrav = Fz  G.Maarde*m/r2 = m * 0,80 * gzeeniveau  6,67.10-11*5,98.1024/r2 = 0,800 * 9,81
r2 = 3,98.1014/7,85 = 5,08.1013  r = 7,13.106 (m). De hoogte boven het aardoppervlak is
7,13.106 – 6,38.106 = 7,5.105 (m) = 7,5.102 (km)
Opgave 26
M * m m * v2
G*M
4 * 2 * r 2
 2 * * r 
2



v




r
r
r2
T2
 T

G*M
G * M r3
Dus:
 2 de constante is dus:
2
4 * 2
4 *
T
2
FG  Fmpz  G *


3
G * M r3
23,5.10 6
6,67.10 11 * M
 2 

 M  6,46.10 23 (kg)
2
2
2
4 *
T
4 *
1,262 * 24 * 3600
Aan het oppervlak van mars geldt: FG = Fz 
M *m
6.67.10 11 * 6,46.10 23
m* g  G

g

 3,76(m / s 2 )
2
6 2
RMars
3,386.10


Opgave 27
R = Raarde + h = 6,378.106 + 1,600.106 = 7,978.106 (m)
M * m m * v2
G*M
FG  Fmpz  G * 2 

 v 2 dus:
r
r
r
6,67.10 11 * 5,976.10 24
v2 
 v  7068(m / s
7,978.10 6
Opgave 28
Je kan weer de 3e wet van Kepler gebruiken:
G * M r3
en T is 24 (h) = 86400 (s)

4 * 2 T 2
6,67.10 11 * 5,976.10 24
* 86400 2  7,537.10 22  r = 4,22.107 (m)
2
4 *
De hoogte boven de aarde is 4,22.107 – 6,378.106 = 3,6.107 (m); ongeveer 36 duizend km
r3 