IJkingstoets burgerlijk ingenieur juli 2015

IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 1
IJkingstoets burgerlijk ingenieur juli 2015: algemene feedback
In totaal namen 791 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden werd aan aspirant-studenten
burgerlijk ingenieur aan de VUB, KU Leuven en UGent.
De toets bestond uit twee delen: een eerste deel bestaande uit 21 enkelvoudige vragen en een tweede deel bestaande
uit samengestelde vragen. Hieronder staan zowel de resultatenverdeling voor het eerste deel, als voor de volledige
toets.
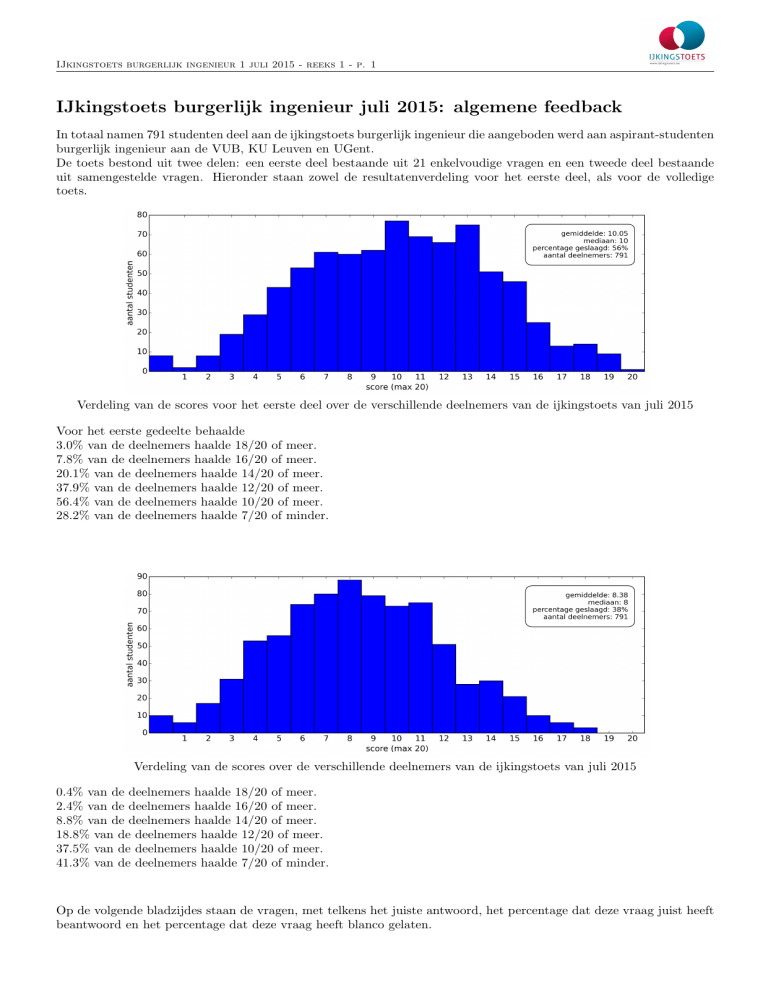
Verdeling van de scores voor het eerste deel over de verschillende deelnemers van de ijkingstoets van juli 2015
Voor het eerste gedeelte behaalde
3.0% van de deelnemers haalde 18/20 of meer.
7.8% van de deelnemers haalde 16/20 of meer.
20.1% van de deelnemers haalde 14/20 of meer.
37.9% van de deelnemers haalde 12/20 of meer.
56.4% van de deelnemers haalde 10/20 of meer.
28.2% van de deelnemers haalde 7/20 of minder.
Verdeling van de scores over de verschillende deelnemers van de ijkingstoets van juli 2015
0.4% van de deelnemers haalde 18/20 of meer.
2.4% van de deelnemers haalde 16/20 of meer.
8.8% van de deelnemers haalde 14/20 of meer.
18.8% van de deelnemers haalde 12/20 of meer.
37.5% van de deelnemers haalde 10/20 of meer.
41.3% van de deelnemers haalde 7/20 of minder.
Op de volgende bladzijdes staan de vragen, met telkens het juiste antwoord, het percentage dat deze vraag juist heeft
beantwoord en het percentage dat deze vraag heeft blanco gelaten.
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 2
Deel 1: Enkelvoudige vragen
Oefening 1
De vijf punten in de onderstaande druk-volume-grafiek stellen vijf verschillende toestanden voor van één mol van een
ideaal gas. Voor een ideaal gas geldt het volgende verband tussen de druk p, uitgedrukt in Pascal, het volume V ,
uitgedrukt in m3 en de temperatuur T , uitgedrukt in Kelvin : pV = nRT ,
waarbij n de hoeveelheid gas in mol voorstelt en R = 8, 31 JK−1 mol−1 de gasconstante is.
Voor welk van deze toestanden bevindt het gas zich op de hoogste temperatuur?
p
A
3p0
(A) toestand A
(B) toestand B
B
2p0
(C) toestand C
C
p0
D
V0
E
2V0
(D) toestand D
(E) toestand E
V
3V0
Oplossing: B
juist beantwoord: 92 %
blanco: 1 %
Oefening 2
a b
a
Beschouw een (2 × 2)-matrix
. Veronderstel dat
c
d
c
a b
2
−2
a b
6
=
. Bereken
.
c d
1
−1
c d
6
(A)
6
6
−6
−6
(B)
(C)
0
0
Oplossing: E
juist beantwoord: 60 %
blanco: 28 %
Oefening 3
1−
Gegeven f : R+
0 → R : x 7→ f (x) = cos (e
0
Bepaal f (x).
(A) f 0 (x) = − sin (e1−
(B) f 0 (x) = − sin (e1−
(C) f 0 (x) = sin (e1−
(D) f 0 (x) =
sin (e
(E) f 0 (x) = sin
√
√
√
x
x
)
x
)e1−
)e1−
√
1− x
Oplossing: D
juist beantwoord: 93 %
blanco: 1 %
x
x
√
√
1− x
)e
√
2 x
√ !
e1− x
√
2 x
√
√
x
√
x
).
(D)
b
d
2
−2
1
2
=
1
2
(E)
en
−2
2
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 3
Oefening 4
Gegeven de punten P (2, 0, 0), Q(0, −3, 0) en R(0, 0, 6) in de driedimensionale ruimte met een cartesiaans assenstelsel
xyz. Het vlak v is het vlak door de punten P , Q en R.
Welk van de volgende punten ligt in het vlak v?
(A) A(1, 1, 1)
(B) B(1, 1, 2)
(C) C(1, 1, 3)
(D) D(1, 1, 4)
Oplossing: E
juist beantwoord: 65 %
blanco: 17 %
Oefening 5
In de figuur hiernaast zie je 3 projecties op 3 onderling loodrechte vlakken van eenzelfde object opgebouwd uit meerdere
identieke kubussen. In de onderstaande figuren zie je 5 objecten getekend in 3 dimensies. Slechts één van deze 5 objecten
kan mits een passende rotatie met alle drie bovenstaande projecties tegelijk overeenkomen. Geef aan welk.
(A)
(C)
(B)
(D)
Oplossing: E
juist beantwoord: 88 %
blanco: 2 %
(E)
(E) E(1, 1, 5)
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 4
Oefening 6
Hoeveel verschillende reële nulpunten heeft de functie f : R → R : x 7→ f (x) = (x3 − 1) ln(x2 + 1) ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Oplossing: B
juist beantwoord: 70 %
blanco: 2 %
Oefening 7
Veronderstel dat x en y complexe getallen zijn die voldoen aan het stelsel
(
(−1 − i)x − 2y = 4
x + (2 − i)y
= i,
waarbij i2 = −1.
Bepaal x + y.
(A) x + y = −1 + 4i
(B) x + y = −1 + 2i
(C) x + y = −1
(D) x + y = 1
(E) x + y kan oneindig veel waarden aannemen.
Oplossing: A
juist beantwoord: 46 %
blanco: 34 %
Oefening 8
De veeltermen f (x) en g(x) zijn veeltermen met reële coëfficiënten. De veelterm f (x) heeft bij deling door x2 + 1 rest
x + 1 en de veelterm g(x) heeft bij deling door x2 + 1 rest x − 1. Welke rest heeft de veelterm f (x) · g(x) bij deling
door x2 + 1?
(A) −2
(B) −1
Oplossing: A
juist beantwoord: 45 %
blanco: 31 %
(C) 0
(D) x − 1
(E) x + 1
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 5
Oefening 9
Gegeven de driedimensionale ruimte met een cartesiaans assenstelsel xyz met daarin het vlak v met vergelijking
x + y + z = 1 en het vlak w met vergelijking x = 0. De rechte l is de doorsnede van de vlakken v en w. De rechte m
is de rechte door de oorsprong, evenwijdig met de rechte l.
Welk van de volgende punten ligt op deze rechte m?
(A) A(1, 1, 1)
(B) B(0, 1, 1)
(C) C(0, 1, 0)
(D) D(0, −1, 0)
Oplossing: E
juist beantwoord: 64 %
blanco: 13 %
Oefening 10
In de figuur hiernaast zie je een grijs object en een zwart kader.
Beeld je in dat het object gesneden wordt door het vlak waarin
het kader zich bevindt. Slechts één van de figuren hieronder
kan het resultaat zijn van deze snede. Geef aan welke.
(A)
(C)
(B)
(D)
Oplossing: B
juist beantwoord: 79 %
blanco: 4 %
(E)
(E) E(0, 1, −1)
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 6
Oefening 11
Gegeven een vlak met een cartesiaans assenstelsel met daarin een cirkel door de drie punten P (0, 0), Q(0, 2) en S(4, 6).
Welk van onderstaande antwoorden geeft de straal r van de cirkel?
√
√
√
√
(A) r = 23
(B) r = 2 6
(C) r = 5
(D) r = 26
(E) r = 3 3
Oplossing: D
juist beantwoord: 63 %
blanco: 26 %
Oefening 12
Beschouw een balk met lengte L. Deze is links ingeklemd en wordt rechts ondersteund. We beschrijven de doorbuiging
van de balk met een functie u : [0, L] → R. De fysische betekenis van de functiewaarde u(x) is de verticale verplaatsing
van het punt op de middellijn van de balk met horizontale coördinaat x. De fysische beperkingen ten gevolge van de
inklemming in x = 0 en de ondersteuning in x = L vertalen zich in vijf wiskundige voorwaarden:
• het linkeruiteinde verplaatst niet: u(0) = 0,
• de helling in het linkeruiteinde is gelijk aan nul: u0 (0) = 0,
• het rechteruiteinde verplaatst niet: u(L) = 0,
• de helling in het rechteruiteinde is niet gelijk aan nul: u0 (L) 6= 0,
• de kromming in het rechteruiteinde is niet gelijk aan nul: u00 (L) 6= 0.
x
u(x)
x=0
x=L
x
Welk van onderstaande functievoorschriften voldoet aan de fysische beperkingen van de balk? α is hierbij een vast
reëel getal verschillend van 0.
x
x
(A) u(x) = α
1−
L
L
x 2 x
(B) u(x) = α
1−
L
L
x 2 x 2
1−
(C) u(x) = α
L
L
x 3
x 4 2
x
(D) u(x) = α 3
−5
+2
L
L
L
πx 2
(E) u(x) = α sin
L
Oplossing: B
juist beantwoord: 52 %
blanco: 21 %
Oefening 13
Wat is het product van de oplossingen van de vergelijking 5x
(A) −14
(B) −12
Oplossing: C
juist beantwoord: 72 %
blanco: 17 %
(C) −10
(D) 10
2
−3x−12
= 0, 04 ?
(E) 12
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 7
Oefening 14
De getallen α en β zijn reële getallen, i2 = −1. Als z1 = 1 − 2i een nulpunt is van de complexe veelterm
z 2 − (α + i)z + (7 + iβ), wat is dan het tweede nulpunt z2 ?
(A) z2 = 1 + 2i
(B) z2 = 1 + i
(C) z2 = 3
(D) z2 = 1 + 3i
(E) z2 = 1 − 3i
Oplossing: D
juist beantwoord: 29 %
blanco: 39 %
Oefening 15
Van een kubus kan je een aantal ribben doorsnijden en dan het
oppervlak openplooien tot een aaneengesloten vlakke figuur.
De figuur hiernaast is daar een voorbeeld van, de buitenzijde
van de kubus wordt zo in één figuur zichtbaar. Slechts één van
de kubussen die hieronder zijn afgebeeld kan NIET leiden tot
deze vlakke figuur. Geef aan welke.
(A)
(C)
(B)
(D)
Oplossing: D
juist beantwoord: 32 %
blanco: 6 %
(E)
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 8
Oefening 16
Een transportband, zoals geschetst in onderstaande figuur, wordt gebruikt om erts te transporteren. De lengte L van
de transportband is 5 m en de breedte B is 0,5 m. De wielen van de transportband hebben een straal r = 0, 5m. Aan
welke snelheid moeten de wielen van de transportband draaien om een gewenst debiet van 10 kg/s af te leveren, als je
weet dat er per vierkante meter van de transportband 20kg erts geladen wordt?
L=5m
(A) π1 toeren per seconde.
B = 0, 5 m
(B) π5 toeren per seconde.
r = 0, 5 m
(C)
1
5π
(D)
2
π
(E)
1
2π
toeren per seconde.
toeren per seconde.
toeren per seconde.
Oplossing: A
juist beantwoord: 59 %
blanco: 10 %
Oefening 17
Precies één van de volgende uitspraken is waar. Welke?
Een vergelijking in x van de vorm a|x| = bx + c met a, b, c reële parameters
(A) heeft voor alle waarden voor a, b en c precies één reële oplossing.
(B) heeft voor alle waarden voor a, b en c precies twee reële oplossingen.
(C) heeft voor alle waarden voor a, b en c één of twee reële oplossingen.
(D) heeft niet voor alle waarden voor a, b en c een reële oplossing.
(E) heeft voor geen enkele waarde voor a, b en c precies één reële oplossing.
Oplossing: D
juist beantwoord: 41 %
blanco: 14 %
Oefening 18
Bij een auto-ongeval met vluchtmisdrijf, herinnert een getuige zich dat de nummerplaat van de gevluchte auto bestaat
uit 3 verschillende letters (allen verschillend van de letter O), gevolgd door 3 cijfers waarvan er juist 2 gelijk zijn (cijfers
0 tot en met 9 zijn mogelijk). Hoeveel mogelijkheden zijn er?
(A) 23 × 35 × 52 × 23
(B) 24 × 34 × 53 × 23
(C) 25 × 34 × 53 × 23
(D) 24 × 33 × 53 × 23
(E) 22 × 58
Oplossing: B
juist beantwoord: 34 %
blanco: 22 %
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 9
Oefening 19
Een tank wordt gevuld met 100 g zout. Er wordt via een eerste toevoerkraan zuiver water toegevoegd. Deze toevoerkraan wordt dichtgedraaid als het volume van de zoutoplossing 50 l bedraagt. Daarna wordt een tweede toevoerkraan
opengedraaid en start de klok. Dit moment komt overeen met tijdstip t = 0 min. Er stroomt dan gedurende 10
minuten een oplossing met een zoutconcentratie van 10 g/l met een constant debiet van 10 l/min in de tank. Er wordt
voortdurend geroerd, zodat de concentratie in de tank op elk moment homogeen is. Welke van onderstaande grafieken
toont het verband tussen de zoutconcentratie c in de tank en de tijd t?
c[g/l]
10
(A)
5
c[g/l]
20
(B)
10
0
c[g/l]
10 t[min]
(C)
8
0
c[g/l]
20
10 t[min]
(D)
6
4
10
2
0
c[g/l]
10 t[min]
(E)
8
6
4
2
0
Oplossing: E
juist beantwoord: 73 %
blanco: 3 %
10 t[min]
0
10 t[min]
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 10
Oefening 20
Rangschik volgende reële getallen van klein naar groot:
Z 1
2
a =
e−(x−1) dx
0
Z
1
2
e−x dx
b =
0
Z
1
c =
2
e−(x+1) dx
0
(A) a < b < c
(B) a = b < c
(C) c < b < a
(D) c < b = a
(E) a = b = c
Oplossing: D
juist beantwoord: 20 %
blanco: 25 %
Oefening 21
Gegeven de functie
Z
x+2π
f : R → R : x 7→ f (x) =
0
Bepaal de waarde van f 0 in
(A) 0
(B)
π
2
Oplossing: C
juist beantwoord: 17 %
blanco: 35 %
2t
dt .
1 + sin2 t
π
2.
(C)
5π
2
(D) 5π
(E) 2
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 11
Deel 2: Samengestelde vragen
De samengestelde oefeningen bestaan telkens uit 3 deelvragen.
Samengestelde oefening 1
Beschouw de gelijkbenige driehoek ABC met tophoek in C. De basis AB van deze driehoek heeft lengte 2L en de
hoogte van deze driehoek is L. De rechthoek DEGF is ingesloten in deze driehoek, met de zijde DE op de zijde AB
en de hoekpunten F en Grespectievelijk op de zijdes AC en BC. De rechthoek heeft een breedte b en een hoogte h.
Door de punten F en G gaat een parabool met top in M , het midden van het lijnstuk AB. Het gebied S is het gebied
boven de parabool dat in de rechthoek DEGF ligt.
C
L
F
G
h
A
D
M
b
E
B
2L
Vraag 22
Bereken de oppervlakte van het gebied S als functie van b√
en h.
(A) 2hb/3
(B) 3hb/4
(C) 5hb/6
(D) 2hb/2
(E)
√
3hb/2
Oplossing: A
juist beantwoord: 35 %
blanco: 46 %
Vraag 23
Bepaal de hoogte h zodat de oppervlakte van het gebied S maximaal is.
√
(A) h = L/4
(B) h = L/3
(C) h = L/2
(D) h = 2L/2
Oplossing: C
juist beantwoord: 20 %
blanco: 64 %
Vraag 24
Bepaal deze maximale oppervlakte.
(A) L2 /3
(B) 2L2 /5
(C) 3L2 /8
Oplossing: A
juist beantwoord: 15 %
blanco: 76 %
(D) 4L2 /9
(E) 5L2 /12
(E) h =
√
3L/2
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 12
Samengestelde oefening 2
Een gelijkbenige driehoek met tophoek 2α is ingeschreven in een cirkel met straal 1 (zie onderstaande figuur).
2α
1
Door α te laten variëren in de tijd, varieert ook de omtrek L van deze driehoek.
Het verband tussen de tijd t en de hoek α is lineair tussen t = 0s en t = 9s. Verder weten we dat op t = 0s de hoek
α = π/12 en dat op t = 9s de hoek α = π/3.
Vraag 25
Bepaal de hoek α op t = 6s.
(A) α = π/10
(B) α = π/9
(C) α = π/8
(D) α = π/6
(E) α = π/4
Oplossing: E
juist beantwoord: 69 %
blanco: 2 %
Vraag 26
Bepaal
√t = 6s.
√ de omtrek L op
(B) 23 3
(A) 3 3
√
(C) 3 2
√
(D) 2 + 2 2
Oplossing: D
juist beantwoord: 46 %
blanco: 34 %
Vraag 27
Bepaal de afname van de omtrek per tijdseenheid op t = 6s.
√
(A) 2 2 per seconde
√
(B) 3 2 per seconde
π
per seconde
36
√
2π
(D)
per seconde
18
√
3π
(E)
per seconde
18
(C)
Oplossing: D
juist beantwoord: 7 %
blanco: 76 %
(E)
√
3+2
IJkingstoets burgerlijk ingenieur 1 juli 2015 - reeks 1 - p. 13
Samengestelde oefening 3
Een mast met een rechthoekig uithangbord is verbonden met de muur van een gemeentehuis. Onderstaande figuur
toont een principeschets in zijaanzicht - de hoeken en de afmetingen zijn dus niet op schaal getekend. De y-as van het
cartesiaans assenstelsel xy stelt de muur van het gemeentehuis voor. In het punt A is de mast met een horizontale
√
verbindingsstaaf vastgemaakt aan de muur van het gemeentehuis. De lengte van de verbindingsstaaf bedraagt 2 3m
en het punt A bevindt zich op een hoogte van 2 m boven het punt O. De totale lengte van de mast OB bedraagt 8,5
m. Het uithangbord is loodrecht op het uiteinde van de mast verbonden en heeft zijden van 2 m en 1 m. Exact in het
midden van het uithangbord staat een zwarte stip M .
y
B
2m
M
√
2 3m
1m
A
HM
2m
x
O
Vraag 28
Welk van de onderstaande antwoorden is de beste benadering voor de hoogte HM van de stip M ?
(A) 3,1 m
(B) 3,5 m
(C) 4,0 m
(D) 6,4 m
(E) 7,5 m
Oplossing: A
juist beantwoord: 38 %
blanco: 9 %
Vraag 29
Welk van onderstaande vectoren is evenwijdig met de rechte BM ?
√
−−→
(A) OP (−1, −5 − 8 3)
√
−−→
(B) OQ(−1, −2 − 3)
√
−−→
(C) OR(1, − 5)
√
−→
(D) OS(1, −8 − 5 3)
√
−→
(E) OT (1, −5 − 8 3)
Oplossing: D
juist beantwoord: 7 %
blanco: 67 %
Vraag 30
−−→
−−→
Wat is het scalair product (inproduct) van de vector OB met de vector BM ?
√
√
(D) -2,125 5 m2
(A) 4,25 m2
(B) -4,25 m2
(C) 2,125 5 m2
Oplossing: B
juist beantwoord: 4 %
blanco: 69 %
(E) 0