IJkingstoets burgerlijk ingenieur juni 2016

IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 1
IJkingstoets burgerlijk ingenieur juni 2016: algemene feedback
Positionering ten opzichte van andere deelnemers
In totaal namen 811 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden werd aan aspirant-studenten
burgerlijk ingenieur aan de VUB, KU Leuven en UGent. 500 deelnemers zijn geslaagd. De figuur hieronder toont de
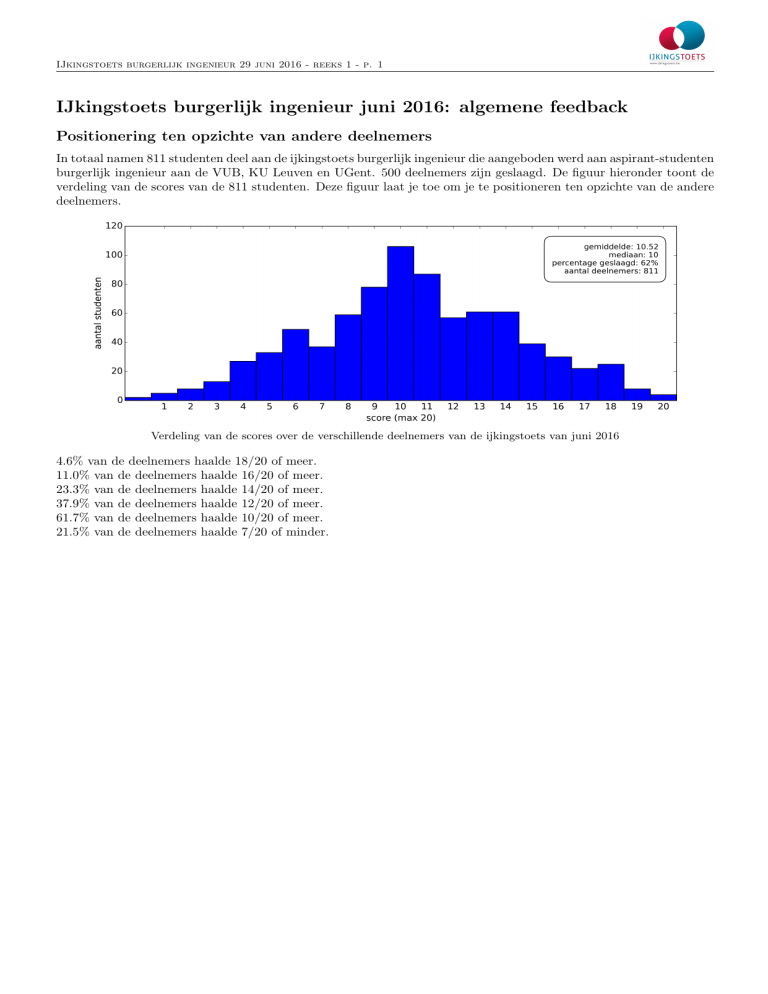
verdeling van de scores van de 811 studenten. Deze figuur laat je toe om je te positioneren ten opzichte van de andere
deelnemers.
Verdeling van de scores over de verschillende deelnemers van de ijkingstoets van juni 2016
4.6% van de deelnemers haalde 18/20 of meer.
11.0% van de deelnemers haalde 16/20 of meer.
23.3% van de deelnemers haalde 14/20 of meer.
37.9% van de deelnemers haalde 12/20 of meer.
61.7% van de deelnemers haalde 10/20 of meer.
21.5% van de deelnemers haalde 7/20 of minder.
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 2
Vervolgtraject voorbije edities
Heel wat van de deelnemers aan de ijkingstoets zijn aan de opleiding bachelor in de ingenieurswetenschappen (KU
Leuven, UGent, VUB) of bachelor in de ingenieurswetenschappen: architectuur (KU Leuven) gestart. De figuur
hieronder toont de studentenstroom tot na de januari-examens. Deze figuur toont dat de wiskundige voorkennis
gemeten tijdens de ijkingstoets, een belangrijke factor is voor je toekomstige studiesucces. Bij de groep die slaagde
op de ijkingstoets heeft een aanzienlijk deel na de januari-zittijd een hoge studie-efficiëntie (groene stroom). Van
studenten uit de groene stroom weten we dat ze bijna allemaal hun bachelor in drie jaar zullen behalen. Een goede
ijkingstoetsscore is echter geen garantie op succes in de opleiding. Hard werken, een goede studieaanpak en motivatie
blijven heel belangrijk! Voor studenten die niet slaagden op de ijkingstoets blijkt het heel moeilijk te zijn om het
bijspijkeren van de voorkennis te combineren met hun studie. Meer dan de helft van de vroegere deelnemers is ofwel al
gestopt met de opleiding in de loop van het eerste semester (zwarte stroom) of heeft een zeer lage studie-efficiëntie in
januari (rode stroom). Van studenten uit de rode stroom weten we dat het heel moeilijk zal zijn om het bachelordiploma
ingenieurswetenschappen te behalen.
Vervolgtraject van de deelnemers aan de voorbije edities van de ijkingstoets.
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 3
Signalen uit het secundair onderwijs
Vanuit het secundair onderwijs heb je ook heel wat waardevolle signalen gekregen die je kunnen ondersteunen bij
je studiekeuze. Het advies van de klassenraad en het percentage wiskunde behaald in het secundair onderwijs zijn
factoren die samen met de score op de ijkingstoets je een zicht kunnen geven op je toekomstig studiesucces. De figuur
hieronder toont hoe het advies van de klassenraad en het percentage wiskunde uit het secundair samenhangt met
studiesucces in de opleiding voor de huidige generatie eerstejaarsstudenten. De kleurschaal geeft aan welk percentage
in deze groep meer dan 30% van de credits uit het eerste semester behaald heeft.
Mooie resultaten wiskunde én een positief advies van de klassenraad voor ingenieurswetenschappen zijn positieve
signalen voor toekomstig studiesucces. Studenten met een lagere score op wiskunde in het secundair onderwijs of die
een negatief advies van de klassenraad kregen, bevinden zich in de gearceerde rechthoek. Deze groep bevat relatief
weinig studenten die in het eerste semester meer dan 30% van de credits behaald hebben.
Verband tussen het advies van de klassenraad, het percentage wiskunde uit het secundair onderwijs en studiesucces in het
eerste semester van de opleiding burgerlijk ingenieur bij 401 eerstejaarsstudenten academiejaar 2015-2016. De oppervlakte van
elke bol is evenredig met het aantal studenten uit de subgroep. De kleurschaal geeft aan welk percentage in de subgroep meer
dan 30% van de credits uit het eerste semester behaald heeft.
Juiste antwoorden en statistieken per vraag
Op de volgende bladzijdes staan de vragen, met telkens het juiste antwoord, het percentage dat deze vraag juist heeft
beantwoord en het percentage dat deze vraag heeft blanco gelaten.
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 4
Oefening 1
Beschouw de veelterm p(x) = (x2 + 3x + 2)(x − 3). Welke van onderstaande uitspraken is geldig?
(A) De veelterm p(x) heeft geen negatieve reële nulpunten.
(B) De veelterm p(x) heeft juist 1 negatief reëel nulpunt.
(C) De veelterm p(x) heeft juist 2 negatieve reële nulpunten.
(D) De veelterm p(x) heeft juist 3 negatieve reële nulpunten.
Oplossing: C
juist beantwoord: 91 %
blanco: 1 %
Oefening 2
Onderstaande figuur toont een driedimensionaal L-vormig voorwerp met zijn afmetingen getekend in perspectief. De
massadichtheid van het materiaal waaruit het voorwerp is gemaakt is 500kg/m3 . Bepaal de massa van dit voorwerp.
(A) 13kg
(B) 15kg
(C) 130kg
(D) 150kg
Oplossing: A
juist beantwoord: 91 %
blanco: 0 %
Oefening 3
Veronderstel dat m 6= 0 een vast natuurlijk getal is. Waaraan is lim
n→+∞
(A) −
1
2
(B) −
1
2m
(C) −
1
2m + 1
Oplossing: D
juist beantwoord: 86 %
blanco: 6 %
Oefening 4
Op welk cijfer eindigt het getal 22017 ?
(A) 2
(B) 4
Oplossing: A
juist beantwoord: 73 %
blanco: 11 %
(C) 6
(D) 8
n
gelijk?
−2m − n
(D) −1
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 5
Oefening 5
Gegeven de punten P (1, −2, 8) en Q(2, −3, 5) in de driedimensionale ruimte. Welk van de volgende punten ligt op de
rechte door de punten P en Q?
(A) het punt A(3, −5, 13).
(B) het punt B(3, −3, −9).
(C) het punt C(3, −5, 3).
(D) het punt D(3, −4, 2).
Oplossing: D
juist beantwoord: 83 %
blanco: 7 %
Oefening 6
Onderstaande figuur geeft de grafiek van de functie f : R → R weer met een volle lijn en de grafiek van de functie
g : R → R met een streepjeslijn. Welk van onderstaande uitspraken is geldig?
3a
(A) f (x) = g(x + 2a)
f (x)
2a
(B) f (x) = g(x) + 2a
(C) f (x) = 2g(x + a)
a
(D) f (x) = 2g(x) + a
g(x)
x
0
Oplossing: D
juist beantwoord: 70 %
blanco: 1 %
Oefening 7
De oplossing van de vergelijking (1 − 2i)(z + 4) = z is het complex getal z = a + bi (i2 = −1, a, b ∈ R). Bepaal b.
(A) b = −4
Oplossing: B
juist beantwoord: 69 %
blanco: 13 %
(B) b = −2
(C) b = 2
(D) b = 4
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 6
Oefening 8
We beschouwen vier verschillende deelverzamelingen van de verzameling H = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}:
• Honeven = {1, 3, 5, 7, 9}
• Hpriem = {2, 3, 5, 7}
• H>2 = {3, 4, 5, 6, 7, 8, 9, 10}
• H<5 = {1, 2, 3, 4}
Bij een spel worden willekeurig twee getallen getrokken uit één en dezelfde van deze vier deelverzamelingen. Elk
getal heeft dezelfde waarschijnlijkheid om getrokken te worden uit deze deelverzameling. De trekking gebeurt met
teruglegging, dit wil zeggen dat beide getallen gelijk kunnen zijn. Het resultaat van de trekking zijn de twee getallen
3 en 5. Uit welke verzameling hebben we met de grootste kans deze twee getallen getrokken?
(A) Honeven
(B) Hpriem
(C) H>2
(D) H<5
Oplossing: B
juist beantwoord: 98 %
blanco: 1 %
Oefening 9
Beschouw de driedimensionale ruimte met een cartesiaans assenstelsel xyz. De verzameling V bevat alle punten
(x, y, z) die voldoen aan z 2 = x2 . De verzameling W bevat alle punten (x, y, z) die voldoen aan x + z = 2. Welke van
onderstaande uitspraken is dan geldig?
(A) De doorsnede van V en W bevat juist één punt.
(B) De doorsnede van V en W is een rechte.
(C) De doorsnede van V en W is een parabool.
(D) De doorsnede van V en W is een vlak.
Oplossing: B
juist beantwoord: 50 %
blanco: 9 %
Oefening 10
Beschouw volgend stelsel met x, y, z ∈ R:

x+y+z
= 2



2x + 3z
= 1
= a
 x + 2y + 3z


3x + 4y + 5z = 4 + 2a
Voor welke waarde van de parameter a heeft dit stelsel precies één oplossing?
(A) a = 2
Oplossing: B
juist beantwoord: 56 %
blanco: 29 %
(B) a = 0
(C) a = −2
(D) a = 7/2
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 7
Oefening 11
Een meetkundige rij is een rij getallen waarvan het quotiënt van twee opeenvolgende elementen een constante is. Deze
constante wordt het quotiënt of de reden van de meetkundige rij genoemd. Beschouw een meetkundige rij waarvan de
7
som van drie opeenvolgende elementen gelijk is aan van het daarop volgend element. Wat is de reden van deze rij?
8
(A) 1
(B)
3
2
(C) 2
(D) 4
Oplossing: C
juist beantwoord: 74 %
blanco: 19 %
Oefening 12
Een kogel vliegt op een bepaald ogenblik met een snelheid ~v met grootte 10 m/s, gericht onder een hoek van 30◦ met
de horizontale. De kogel ondervindt een versnelling ~g met een grootte 10 m/s2 , gericht verticaal naar beneden. De
tangentiële versnelling is de loodrechte projectie van de versnelling ~g op de as evenwijdig met de snelheid ~v . Geef de
grootte van de tangentiële versnelling van de kogel op dat ogenblik.
~v
(A) 0 sm2
30◦
(B) 0.5 sm2
90
◦
~g
(C) 5 sm2
√
(D) 5 3
m
s2
Oplossing: C
juist beantwoord: 45 %
blanco: 26 %
Oefening 13
Beschouw het vlak met cartesiaans assenstelsel xy met de x-as horizontaal naar rechts en de y-as verticaal naar boven.
Hieronder worden alle hoeken gemeten vanaf de positieve x-as. We gebruiken de conventie dat hoeken in tegenwijzerzin
positief zijn, en dat hoeken in wijzerzin negatief zijn. Het punt P heeft coördinaten (0, 1). Het punt Q ligt op een
−−→
afstand 4 van de oorsprong O en de vector OQ maakt een hoek van −π/6 met de positieve x-as. De hoek α is de hoek
−−→
die de vector P Q maakt met de positieve x-as. Bepaal tan α.
√
(A) tan α = − 3/2
√
(B) tan α = −2 2/3
√
(C) tan α = −3 3/8
√
(D) tan α = −3 2/4
Oplossing: A
juist beantwoord: 45 %
blanco: 46 %
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 8
Oefening 14
Beschouw de functie f met als voorschrift
x 7→ f (x) = −x2 + 6x − 3
f :R→R:
x 7→ f (x) = 2x
als x ≤ 3
als x > 3
Bepaal f −1 (5).
(A) f −1 (5) = 1/10
(B) f −1 (5) = 2
(C) f −1 (5) = 5/2
(D) f −1 (5) = 4
Oplossing: B
juist beantwoord: 19 %
blanco: 16 %
Oefening 15
Kaat wil een pakket omhoog hijsen. Ze hangt hiervoor het pakket aan een touw dat rond een balk hangt. De balk
hangt op 5 meter hoogte boven de grond en kan niet bewegen. In de beginsituatie ligt het pakket op de grond. Kaat
houdt het touw strak gespannen vast op 1 meter boven de grond, en staat 3 meter rechts van het pakket. Daarna
loopt ze naar rechts. Ze laat het touw niet los en blijft het touw op 1 meter hoogte houden. Het touw glijdt over de
balk en het pakket schuift naar boven. Als Kaat 1 meter opgeschoven is naar rechts, welke van onderstaande waarden
is dan de beste benadering voor de afstand waarover het pakket naar boven geschoven is?
De dikte van de balk mag verwaarloosd worden t.o.v. de andere gegeven afmetingen. De figuur hieronder is een
principetekening van de beginsituatie, de afmetingen zijn niet in de juiste verhoudingen getekend.
(A) 0,5 meter
(B) 0,65 meter
(C) 0,8 meter
Oplossing: B
juist beantwoord: 62 %
blanco: 13 %
Oefening 16
Gegeven is de functie f : R → R : x 7→ f (x) =
Welke van volgende uitspraken is geldig?
(A) De functie f is overal stijgend.
(B) De functie f is overal dalend.
(C) De functie f heeft een maximum.
(D) De functie f heeft een minimum.
Oplossing: B
juist beantwoord: 55 %
blanco: 6 %
√
x2 + 5 − x.
(D) 0,95 meter
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 9
Oefening 17
√
3
3
1 − x2
dx.
1 − x4
0
Welk van onderstaande uitspraken is geldig?
Z
Stel I =
(A) 0, 5 < I ≤ 0, 6
(B) 0, 6 < I ≤ 0, 7
(C) 0, 7 < I ≤ 0, 8
(D) 0, 8 < I ≤ 0, 9
Oplossing: A
juist beantwoord: 57 %
blanco: 34 %
Oefening 18
Een kinderzwembad heeft een vlakke, horizontale bodem met een oppervlakte van van 4,2 m2 . Alle wanden van het
zwembad staan verticaal. Op tijdstip t = 0 is het zwembad leeg. Het zwembad wordt gevuld met water met een debiet
Q dat tijdsafhankelijk is. De afhankelijkheid tussen het debiet Q (gegeven in liter per minuut) en de tijd t (gegeven
in minuten) is gegeven in onderstaande grafiek. Op welk tijdstip is het zwembad gevuld tot een hoogte van 20 cm?
Q(t) [l/min]
30
0
0 2
(A) t = 27 min
Oplossing: C
juist beantwoord: 66 %
blanco: 5 %
(B) t = 28 min
10
20
(C) t = 29 min
30
t [min]
(D) t = 30 min
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 10
Oefening 19
Gegeven I1 =
R0
−a
(| − x| − x) dx en I2 =
Ra
0
(| − x| − x) dx, waarbij a > 0.
Welke van volgende uitspraken is geldig?
(A) I1 > I2
(B) I1 < I2
(C) I1 = I2 > 0
(D) I1 = I2 < 0
Oplossing: A
juist beantwoord: 55 %
blanco: 14 %
Oefening 20
Beschouw het vlak met een cartesiaans assenstelsel xy. De verzameling V is de verzameling van alle punten (x, y) die
voldoen aan (x − 3)2 + (y + 1)2 = 4. De rechte r is de rechte door de punten (0, −1) en (3, 2).
Welke van onderstaande uitspraken is geldig?
(A) De doorsnede van V en r is leeg.
(B) De doorsnede van V en r bevat juist 1 punt.
(C) De doorsnede van V en r bevat juist 2 punten.
(D) De doorsnede van V en r bevat meer dan 2 punten.
Oplossing: A
juist beantwoord: 70 %
blanco: 5 %
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 11
Oefening 21
Omdat een grafisch afdrukapparaat enkel rechte lijnen kan afdrukken, wordt een cirkel benaderd door een ingeschreven
regelmatige veelhoek. De straal van de te benaderen cirkel bedraagt 80 mm. Men wenst dat de afstand tussen een
zijde van de veelhoek en het punt O hoogstens 0,1 mm afwijkt van de gewenste 80 mm. Wat is het kleinst mogelijk
aantal hoeken van de regelmatige veelhoek die voldoet aan deze precisie?
Je mag bij je berekeningen volgende benaderingen voor kleine waarden van α (in radialen) gebruiken:
sin α ≈ α
(A) 48
cos α ≈ 1 −
(B) 53
(C) 58
α2
2
(D) 63
Oplossing: D
juist beantwoord: 25 %
blanco: 64 %
Oefening 22
Z
Stel a is de oplossing van volgende vergelijking met x ∈ R:
Welke van onderstaande uitspraken is geldig?
(A) a < − ln 3
(B) − ln 3 ≤ a < 0
(C) 0 ≤ a < ln 3
(D) ln 3 ≤ a
Oplossing: A
juist beantwoord: 33 %
blanco: 28 %
0
x
et dt = 5ex − 2.
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 12
Oefening 23
Op een autosnelweg rijden twee vrachtwagens op een bepaald ogenblik (stel t = 0) met eenzelfde snelheid naast elkaar,
met de voorwielen op één lijn. De snelheid van deze vrachtwagens wordt voor de volgende vier minuten voorgesteld
in onderstaande figuur.
Het tijdstip t1 is het eerste tijdstip waarbij de vrachtwagens opnieuw naast elkaar rijden met de voorwielen op één
lijn. In welk interval ligt het tijdstip t1 ?
(A) 2 min < t1 ≤ 2,5 min.
(B) 2,5 min < t1 ≤ 3 min.
(C) 3 min < t1 ≤ 3,5 min.
(D) 3,5 min < t1 ≤ 4 min.
Oplossing: C
juist beantwoord: 42 %
blanco: 20 %
Oefening 24
Bepaal m ∈ R zodat het getal 3 i43 − 2m i42 + (1 − m) i41 + 5 reëel is. i2 = −1
(A) -2
(B) 0
Oplossing: A
juist beantwoord: 71 %
blanco: 8 %
(C) 1
(D) 4
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 13
Oefening 25
Beschouw de functie f met als voorschrift
x 7→ f (x) = −x2 + a als x ≤ 2
f :R→R:
,
x 7→ f (x) = x − 1
als x > 2
met a zo dat de functie f continu is in 2. Hoeveel nulpunten heeft de functie f ?
(A) 0
(B) 1
(C) 2
(D) 3
Oplossing: B
juist beantwoord: 52 %
blanco: 6 %
Oefening 26
Stel a = −
π
.
10e
Welke van volgende uitspraken is geldig?
(A) a < sin a < ln(−a)
(B) sin a < a < ln(−a)
(C) ln(−a) < sin a < a
(D) ln(−a) < a < sin a
Oplossing: D
juist beantwoord: 27 %
blanco: 30 %
Oefening 27
Welk functievoorschrift kan bij volgende grafiek horen?
Oplossing: B
juist beantwoord: 56 %
blanco: 24 %
(A) f (x) =
x5 − 1
x3 − x
(B) f (x) =
x5 + 1
5x3 − 20x
(C) f (x) =
x5 − 1
2x3 − 8x
(D) f (x) =
x5 + 1
x3 − x
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 14
Oefening 28
" 2
2 #
2
1
0
1
n−1
Bepaal lim
+
+ ··· +
n→+∞ n
n
n
n
Hint: onderstaande figuur.
(A) 0
(B)
1
3
(C)
1
2
(D) 1
Oplossing: B
juist beantwoord: 23 %
blanco: 29 %
Oefening 29
De figuur toont een vlak met cartesiaans assenstelsel xy met daarin een driehoek ABC. Verder is een lineaire
transformatie T gegeven met als voorschrift
u
1 1
x
(1)
T (x, y) =
=
v
−1 1
y
Na toepassing van de transformatie T op alle punten van de driehoek ABC vinden we een nieuwe driehoek DEF .
Bepaal de oppervlakte van deze driehoek DEF .
y
C(0, 2)
A(0, 0)
(A) 1
x
B(1, 0)
(B) 2
Oplossing: B
juist beantwoord: 55 %
blanco: 22 %
(C) 3
(D) 4
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 15
Oefening 30
De vergelijking 2 cos2 α + 3 cos α + 1 = 0 heeft twee verschillende oplossingen α1 en α2 die behoren tot het interval
[0, π]. Bepaal sin(α1 + α2 ).
√
√
(A) −1
(B) − 3/2
(C) 3/2
(D) 1
Oplossing: B
juist beantwoord: 65 %
blanco: 17 %
Oefening 31
Oplossing: C
juist beantwoord: 83 %
blanco: 9 %
IJkingstoets burgerlijk ingenieur 29 juni 2016 - reeks 1 - p. 16
Oefening 32
Oplossing: C
juist beantwoord: 83 %
blanco: 3 %
Wij zijn geı̈nteresseerd in uw mening!
Nam u deel aan deze ijkingstoets? Dan zouden we willen vragen om uw mening over dit feedback-document met ons
te delen via deze link.