IJkingstoets burgerlijk ingenieur september 2014

IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 1
IJkingstoets burgerlijk ingenieur september 2014: algemene feedback
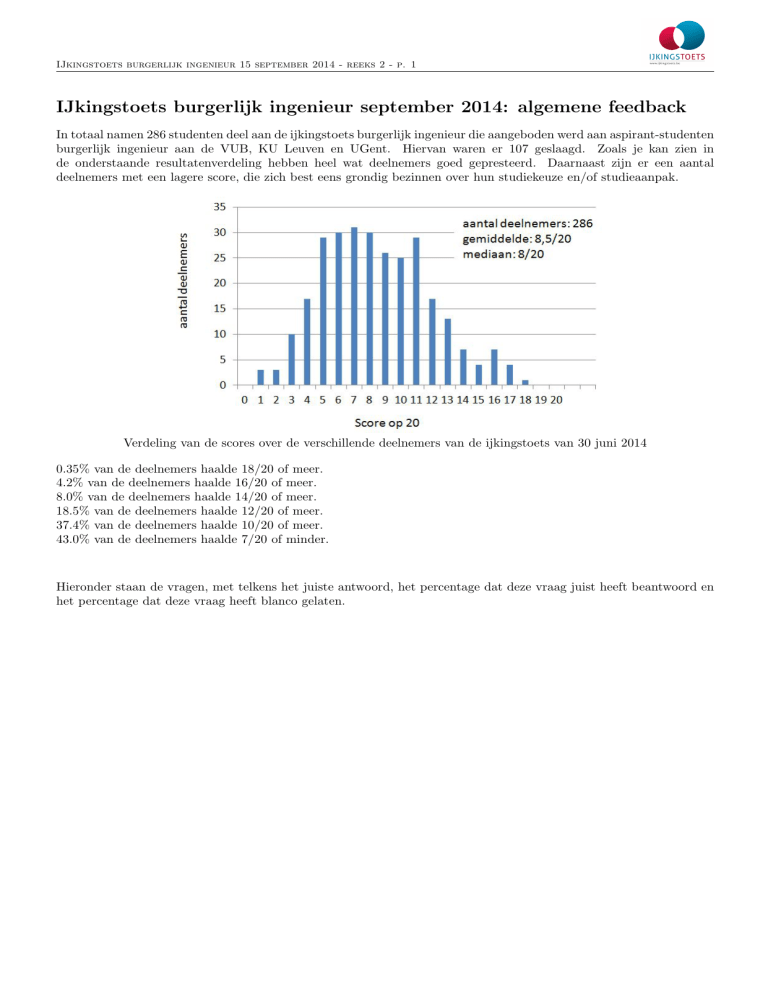
In totaal namen 286 studenten deel aan de ijkingstoets burgerlijk ingenieur die aangeboden werd aan aspirant-studenten
burgerlijk ingenieur aan de VUB, KU Leuven en UGent. Hiervan waren er 107 geslaagd. Zoals je kan zien in
de onderstaande resultatenverdeling hebben heel wat deelnemers goed gepresteerd. Daarnaast zijn er een aantal
deelnemers met een lagere score, die zich best eens grondig bezinnen over hun studiekeuze en/of studieaanpak.
Verdeling van de scores over de verschillende deelnemers van de ijkingstoets van 30 juni 2014
0.35% van de deelnemers haalde 18/20 of meer.
4.2% van de deelnemers haalde 16/20 of meer.
8.0% van de deelnemers haalde 14/20 of meer.
18.5% van de deelnemers haalde 12/20 of meer.
37.4% van de deelnemers haalde 10/20 of meer.
43.0% van de deelnemers haalde 7/20 of minder.
Hieronder staan de vragen, met telkens het juiste antwoord, het percentage dat deze vraag juist heeft beantwoord en
het percentage dat deze vraag heeft blanco gelaten.
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 2
Oefening 1
Mats en Sien vertrekken samen met de fiets voor een tocht van 50 km. Mats fietst 10% sneller dan Sien en komt een
kwartier vroeger aan. Hoe lang doet Sien over de tocht van 50 km?
(A) 1 uur en 45 minuten
(B) 2 uur
(C) 2 uur en 15 minuten
(D) 2 uur en 30 minuten
(E) 2 uur en 45 minuten
Oplossing: E
juist beantwoord: 39 %
blanco: 16 %
Oefening 2
2
Bepaal
√ de oppervlakte√van de figuur die bestaat uit de punten (x, y) van R die voldoen aan |x| + |y| ≤ 2
(A) 2 2
(B) 4 2
(C) 4
(D) 8
(E) 16
Oplossing: D
juist beantwoord: 38 %
blanco: 37 %
Oefening 3
h
√ i
Bepaal sin Bgcos − 23 .
(A) −1/2
(B) 1/2
√
(C) − 3/2
(D)
√
2/2
(E)
√
3/2
Oplossing: B
juist beantwoord: 66 %
blanco: 12 %
Oefening 4
Welke van onderstaande functies is de afgeleide van de functie met voorschrift f (x) =
(A) g(x) =
xex −1
ex
(B) g(x) =
ex −1
ex
(C) g(x) =
ex +1
ex
(D) g(x) =
ex −1
e2x
(E) g(x) =
e2x −1
e2x
Oplossing: B
juist beantwoord: 73 %
blanco: 5 %
xex +1
ex ?
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 3
Oefening 5
Beschouw het gebied tussen de parabool met vergelijking y = x2 − 2x + 2, de raaklijn aan deze parabool in het punt
(3, 5) en de coördinaatassen. De oppervlakte van dit gebied is gelijk aan:
(B) 25
(C) 59
(D) 73
(E) 84
(A) 23
8
8
8
8
8
Oplossing: A
juist beantwoord: 36 %
blanco: 47 %
Oefening 6
De vier zijden van een gelijkzijdige piramide, ook wel viervlak en tetrader genoemd, zijn toch van elkaar te onderscheiden doordat ze een verschillende markering kregen: ze zijn gedeeltelijk ingekleurd of met een lijn gekenmerkt.
Als bovenstaande figuren 3 zichten zijn op die piramide, welk van onderstaande 5 zichten is dan een mogelijk 4e zicht
op die piramide?
(A)
(B)
(D)
(E)
Oplossing: E
juist beantwoord: 48 %
blanco: 25 %
(C)
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 4
Oefening 7
√
Gegeven is de functie f met voorschrift f : R+ → R : x 7→ y = x2 − 6 x − 5.
Verder is de rechte l de rechte door de punten P (1, 2) en Q(2, 1).
Welke is de x-coördinaat van het snijpunt van de grafiek van de functie f met de rechte l?
(A) −10
(B) 1
(C) 2
(D) 4
(E) 9
Oplossing: D
juist beantwoord: 76 %
blanco: 16 %
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 5
Oefening 8
De grafiek van de reële functie f is gegeven in onderstaande figuur.
f (x)
1
0
x
1
Van de reële functie g weten we dat voor alle x geldt dat g(x) = f (x2 ). Welk van onderstaande figuren geeft de grafiek
van de functie g weer.
g(x)
g(x)
1
1
0
(A)
1
0
x
g(x)
g(x)
1
1
0
(C)
1
x
1
x
(D)
g(x)
1
0
(E)
Oplossing: E
juist beantwoord: 17 %
blanco: 10 %
0
x
1
(B)
1
x
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 6
Oefening 9
Welk bovenaanzicht kan bij onderstaand vooraanzicht horen?
(A)
(B)
(D)
(E)
(C)
Oplossing: D
juist beantwoord: 81 %
blanco: 4 %
Oefening 10
√
Noem |z| = a2 + b2 de modulus of absolute waarde van het complexe getal z = a + ib, met a en b reële getallen en
i2 = −1. Noem u en v de twee complexe oplossingen van de vergelijking in de complexe veranderlijke x:
x2 + (3 + 2i)x − 1 + 3i = 0.
Dan is |u − v| gelijk aan
√
√
(A) 1
(B) 3
(C) 4
(D) 10 − 1
(E) 10 + 1
Oplossing: B
juist beantwoord: 59 %
blanco: 31 %
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 7
Oefening 11
Een voorwerp beweegt op een horizontale as. Zijn positie x (uitgedrukt in meter) wordt als functie van de tijd t
1
(uitgedrukt in seconden) gegeven door x(t) = 20
cos(πt).
Bereken de lengte van de weg die het voorwerp aflegt gedurende de eerste 15 seconden.
(A) −0, 05 m
(B) 0, 05 m
(C) 0.75 m
(D) 1.5 m
(E) 30 m
Oplossing: D
juist beantwoord: 27 %
blanco: 18 %
Oefening 12
Tot welk van de vijf onderstaande gesloten volumes kan je deze vlakke figuur vouwen? Je kan enkel op de getekende
lijnen vouwen.
(A)
(B)
(D)
(E)
Oplossing: D
juist beantwoord: 59 %
blanco: 24 %
(C)
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 8
Oefening 13
De onderstaande figuur toont de grafiek van drie verschillende reële functies f , g en h. Eén van onderstaande verbanden
is geldig, welk?
(A) f = h0 = g 00
(B) h = g 0 = f 00
(C) g = f 0 = h00
(D) f = g 0 = h00
(E) g = h0 = f 00
Oplossing: D
juist beantwoord: 58 %
blanco: 4 %
Oefening 14
De functie sinh (sinus hyperbolicus) is gedefinieerd als
sinh : R → R : x 7→
ex − e−x
.
2
Geef de oplossingen van de volgende vergelijking in de reële veranderlijke x: sinh(ln x) = 21 .
(B)
√
1+ 5
2
√
1− 5
2
(C)
1
2
(A)
√
√
(D) { 1+2 5 , 1−2 5 }
(E) 1
Oplossing: A
juist beantwoord: 18 %
blanco: 22 %
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 9
Oefening 15
Beschouw in het xy-vlak de rechte r met vergelijking 2x+3y +1 = 0. Bepaal de vergelijking van de rechte die loodrecht
staat op r, en die door het punt (1, 1) gaat.
(A) 3x − 2y − 1 = 0
(B) 2x − 3y + 1 = 0
(C) 3x − 2y + 1 = 0
(D) 2x − 3y + 5 = 0
(E) 2x + 3y − 5 = 0
Oplossing: A
juist beantwoord: 83 %
blanco: 3 %
Oefening 16
Onderstaande figuur geeft een schets van een stad weer met daarop twee mogelijke wegen om je tussen een startpunt
en eindpunt te verplaatsen: er is een cirkelvormige ringweg en een rechte weg door de stad. Een wagen heeft voor
het traject over de ringweg een gemiddelde snelheid v1 . Voor het traject langs de rechte weg door de stad heeft deze
wagen een gemiddelde snelheid v2 . Wat is de voorwaarde waaraan v1 en v2 moeten voldoen opdat de route door de
stad even veel tijd kost als de route langs de ringweg?
weg
r in g
start
eg
te w
h
c
4
re
3π /
=
α
Oplossing: A
juist beantwoord: 44 %
blanco: 37 %
einde
(A)
v1
v2
= √3π √
(B)
v1
v2
= √3π √
(C)
v1
v2
=
3π
√
2 2
(D)
v1
v2
=
3π
√
4 2
(E)
v1
v2
=
3π
√
8 2
4
8
2+ 2
2+ 2
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 10
Oefening 17
Welk van de 5 aanzichten is niet van onderstaand volume?
(A)
(B)
(D)
(E)
Oplossing: B
juist beantwoord: 31 %
blanco: 24 %
(C)
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 11
Oefening 18
Beschouw de volgende figuur, waarin AB k CD. De getallen geven de lengtes van de bijhorende lijnstukken weer.
9
2
3
A
C
Bepaal de lengte van het lijnstuk BD.
(A) 6
(B) 6,25
(C) 6,50
Oplossing: D
juist beantwoord: 50 %
blanco: 42 %
2
3
B
D
5
(D) 6,75
(E) 7
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 12
Oefening 19
Een klassieke manier om informatie (draadloos) door te sturen is de amplitude van een golf veranderen over de tijd.
In de volgende figuur wordt de grafiek van de golffunctie f (t) getoond.
f (t)
2
Wat is het functievoorschrift voor f ?
(A) f (t) = 1 + cos(20t) sin(20t)
1
(B) f (t) = 1 + sin(20t) cos(t)
(C) f (t) = cos(20t) cos(t)
(D) f (t) = 1 + cos(20t) sin(t)
0
π
0
2π
t
(E) f (t) = 1 + sin(20t) cos(t)
Oplossing: B
juist beantwoord: 42 %
blanco: 35 %
Oefening 20
Een stuk glas heeft als vorm een gelijkzijdige driehoek met zijde L. Het is de bedoeling om dit stuk glas te versnijden,
zodat kleinere stukjes ontstaan, die elk gelijkzijdige driehoeken zijn, met zijde L/n. Het versnijden gebeurt volgens
het patroon dat in onderstaande figuur weergegeven is voor n = 5. De streepjeslijnen in de figuur zijn de snijlijnen.
Wat is de totale lengte van alle snijlijnen in het geval L = 1m en n = 20?
L
L/n
(A) 27m
(B) 28, 5m
Oplossing: B
juist beantwoord: 54 %
blanco: 21 %
(C) 30m
(D) 31, 5m
(E) 33m
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 13
De samengestelde oefeningen bestaan telkens uit 3 deelvragen.
Samengestelde oefening 1
We vormen ‘woorden’ van 6 letters met de letters van het woord ‘lokaal’. In deze context is een ‘woord’ een willekeurige
lettercombinatie, die dus niet noodzakelijk een zinvolle betekenis heeft.
Vraag 21
Hoeveel dergelijke ’woorden’ kunnen er worden gevormd?
(A) 120
(B) 180
(C) 360
(D) 720
(E) 840
Oplossing: B
juist beantwoord: 57 %
blanco: 16 %
Vraag 22
Als men alle gevormde ‘woorden’ alfabetisch rangschikt, op de hoeveelste plaats staat dan ‘koalla’
(A) 86e
(B) 87e
(C) 146e
(D) 147e
(E) 171e
Oplossing: B
juist beantwoord: 34 %
blanco: 44 %
Vraag 23
Hoeveel van deze ‘woorden’ starten NIET met ‘l’ ?
(A) 30
(B) 60
(C) 90
(D) 120
(E) 150
Oplossing: D
juist beantwoord: 49 %
blanco: 36 %
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 14
Samengestelde oefening 2
De Gumbel-distributie is een gekende functie uit de statistiek. Ze heeft als voorschrift
g : R → R : x 7→ e−(x+e
−x
)
Vraag 24
Bepaal g(0)
(A) g(0) = 0
(B) g(0) = 1
(C) g(0) = e
(D) g(0) = 1/e
(E) g(0) = −e
Oplossing: D
juist beantwoord: 97 %
blanco: 1 %
Vraag 25
Bepaal de afgeleide g 0 (0)
(A) g 0 (0) = 0
(B) g 0 (0) = 1
Oplossing: A
juist beantwoord: 70 %
blanco: 14 %
Vraag 26
Welke van volgende uitspraken is correct?
(A) g(−100) < g(0) < g(e) < g(π)
(B) g(−100) < g(e) < g(π) < g(0)
(C) g(π) < g(e) < g(0) < g(−100)
(D) g(−100) < g(π) < g(e) < g(0)
(E) g(0) < g(e) < g(π) < g(−100)
Oplossing: D
juist beantwoord: 43 %
blanco: 19 %
(C) g 0 (0) = e
(D) g 0 (0) = 1/e
(E) g 0 (0) = −e
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 15
Samengestelde oefening 3
Een vrachtwagen heeft een haakarm ABC om een container te kunnen opladen. De arm roteert rond een horizontale
as A die vast is aan de vrachtwagen. De arm ABC vormt een rechte hoek. De rotatie van de arm wordt gestuurd door
een hydraulische zuiger ED, met het punt D vast op de vrachtwagen en het punt E vast op de haakarm. De lengte
van de hydraulische zuiger is instelbaar, en deze bepaalt de hoek α tussen het deel AB van de arm en de horizontale.
De tabel geeft de coördinaten, zoals ze zijn uitgedrukt in het assenstelsel met oorsprong ter hoogte van het wegdek,
en onder de achterste rand van de vrachtwagen.
A
D
AB
BC
AE
coördinaten
x [mm]
2500
6000
afmetingen [mm]
4500
2000
1200
y [mm]
1000
800
De tekening is een principe-tekening en is niet
op schaal getekend.
Vraag 27
Als de vrachtwagen stil staat en de zuiger uitgeschoven wordt, welke baan volgt het punt C dan?
(A) een cirkelboog
(B) een stuk van een ellips
(C) een lijnstuk dat niet horizontaal of vertikaal staat
(D) een horizontaal lijnstuk
(E) een vertikaal lijnstuk
Oplossing: A
juist beantwoord: 73 %
blanco: 6 %
Vraag 28
Welke van onderstaande waarden is de beste benadering voor de x-coördinaat van het punt C op het moment dat de
hoek α = 60◦ .
(A) xC = 2100mm
(B) xC = 3000mm
(C) xC = 4300mm
(D) xC = 5400mm
(E)
xC = 6000mm
Oplossing: B
juist beantwoord: 27 %
blanco: 45 %
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 16
Vraag 29
Welke van onderstaande waarden is de beste benadering voor de de lengte van de zuiger op het moment dat de hoek
α = 0◦ .
(A) 2300mm
(B) 2500mm
(C) 2800mm
(D) 3100mm
(E) 3400mm
Oplossing: A
juist beantwoord: 33 %
blanco: 43 %
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 17
Samengestelde oefening 4
Beschouw de veelterm p(x) = 2x4 + ax3 + bx2 + cx − 2, met reële coëfficiënten a, b en c zodanig dat deze veelterm
deelbaar is door (x + 1)(x − 2) en zodat p(−2) = 36.
Vraag 30
Welke van volgende uitspraken is geldig?
(A) a − b + c = 0
(B) p(1) = 0
(C) a + b − c = −3
(D) a − b − c = −2
(E) p(1) = −4
Oplossing: A
juist beantwoord: 60 %
blanco: 31 %
Vraag 31
Bepaal de afgeleide p0 (1)
(A) p’(1)=-5
(B) p’(1)=-3
(C) p’(1)=-1
(D) p’(1)=1
(E) p’(1)=5
Oplossing: A
juist beantwoord: 37 %
blanco: 53 %
Vraag 32
De veelterm q(x) is het resultaat van de deling van p(x) door (x + 1)(x − 2). Bepaal de afgeleide q 0 (0).
(A) q 0 (0) = −2
(B) q 0 (0) = 0
(C) q 0 (0) = 1
(D) q 0 (0) = 3
(E) q 0 (0) = 5
Oplossing: B
juist beantwoord: 35 %
blanco: 57 %
IJkingstoets burgerlijk ingenieur 15 september 2014 - reeks 2 - p. 18
Samengestelde oefening 5
Gegeven de 3 punten P (0, 0, 4), Q(0, 3, 0), en R(−1, 2, 1), en de rechte
l ↔ {x = y + 1, x + y + z = 3} in de driedimensionale ruimte met een cartesiaans assenstelsel.
Vraag 33
−−→
−→
De vector P Q is de vector van het punt P naar het punt Q. De vector P R is de vector van het punt P naar het punt
−−→
−→
R. Noem α de hoek tussen de vectoren P Q en P R. Welke uitspraak is dan geldig?
(A) cos α ≤ 0.2
(B) 0.2 < cos α ≤ 0.4
(C) 0.4 < cos α ≤ 0.6
(D) 0.6 < cos α ≤ 0.8
(E) 0.8 < cos α
Oplossing: E
juist beantwoord: 58 %
blanco: 23 %
Vraag 34
De doorsnede van de rechte l met het vlak dat door de drie punten P, Q en R loopt, noemen we D. yD is de
y-coördinaat van dit punt D. Welke van onderstaande uitspraken is dan geldig?
(A) Er is geen snijpunt D.
(B) yD < −2
(C) −2 ≤ yD < 0
(D) 0 ≤ yD < 2
(E) 2 ≤ yD
Oplossing: B
juist beantwoord: 19 %
blanco: 49 %
Vraag 35
Zoek een punt S op de rechte l zodanig dat de rechte SP loodrecht staat op de rechte SR. Noem xS de x-coördinaat
van het punt S. Welke van volgende uitspraken is geldig?
(A) Er bestaat geen dergelijk punt.
(B) xS ≤ −1/2
(C) −1/2 < xS < 0
(D) 0 ≤ xS < 1/2
(E) 1/2 ≤ xS
Oplossing: E
juist beantwoord: 13 %
blanco: 73 %