Afleiding van de Wet van Arbeid en Kinetische Energie

Afleiding van de Wet van Arbeid en Kinetische Energie
Opgaven die te maken hebben met arbeid en energie kun je oplossen met de wet van behoud van
energie. Zie daarvoor het boek. Een andere manier is de hieronder afgeleide wet van arbeid en
kinetische energie.
Een kracht die arbeid verricht op een voorwerp draagt energie over aan dat voorwerp. Het aantal joule
dat een kracht aan positieve arbeid toevoert aan het voorwerp komt ten goede aan de beweging van het
voorwerp. Als een kracht negatieve arbeid verricht, onttrekt hij juist energie aan dat voorwerp
waardoor het langzamer zal gaan bewegen. Verrichte arbeid en snelheid (kinetische energie) hebben
dus van alles met elkaar te maken. Dat kun je zien in de volgende afleiding.
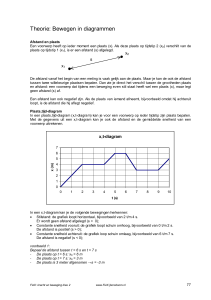
Neem een kracht F die op een voorwerp werkt. Het voorwerp heeft een massa m en een beginsnelheid
vbegin. Na een bepaalde verplaatsing s heeft het voorwerp de snelheid veind.
F
s
We berekenen de arbeid van de kracht. Die is gelijk aan F s want de kracht heeft dezelfde richting
als de verplaatsing (dus  = 0° en cos = 1), dus:
W = F  s = m a s (uit de tweede wet van Newton: F = m a)
We kijken nu naar een tijdsinterval t. Dan volgt met a = v/t en s = vgem t:
W = (m v/t) (vgem t) = m v vgem
(t kun je wegdelen)
Met v = veind - vbegin en vgem = ½ (veind + vbegin) (gewoon gemiddelde nemen van 2 getallen) volgt:
W = m (veind - vbegin) ½ (veind + vbegin) = ½ m (veind-vbegin)(veind+vbegin)
Haakjes wegwerken of gebruik maken van de wiskundige regel (a-b)(a+b) = a² - b² levert:
W = ½ m (veind² - vbegin²) = ½ m veind² - ½ m vbegin² = Ek,eind - Ek,begin = Ek
Heb je meer dan een kracht, dan moeten de arbeidjes van de verschillende krachten bij elkaar opgeteld
worden: dan wordt dit geschreven als WOP (spreek uit: som van alle arbeid op het voorwerp)
Dus de totale verrichte arbeid op een voorwerp komt overeen met de verandering van kinetische
energie. Dit is de wet van arbeid en kinetische energie. In formulevorm:
W
op
  Ek
W
op

1 2
1 2
mveind  mvbegin
2
2
Voor toepassing zie ommezijde.
Toepassing:
Een slee wordt een helling opgetrokken door Karel. Op de slee zit Marie. De totale massa van de slee
en Marie is 60 (kg). De hellingshoek is 5,0°. Karel levert een trekkracht van 80 (N) langs de helling
omhoog. De wrijvingskracht is 15 (N). De helling is 20 (m) lang. Bereken de snelheid van de slee
boven aan de helling als de snelheid beneden 2,0 (m/s) is.
Oplossing:
Stap 1: Maak een tekening met alle gegevens en krachten.
vbegin = 2,0 (m/s)
m = 60 (kg)
Dus Fz = 60 · 9,81 = 588,6 (N)
Stap 2: Bereken de arbeid van alle krachten:
Er zijn vier krachten, dus ook vier keer een verrichte arbeid
•
Arbeid van de normaalkracht: geen arbeid (kracht loodrecht op verplaatsing). W N = 0 (J)
•
Arbeid van de wrijvingskracht: WW = FW  s  cos (180) = 15  20  -1 = - 300 (J)
•
Arbeid van de zwaartekracht: WZ = FZ s  cos  = 588,6  20  cos (95) = -1025 (J)
•
Arbeid van de trekkracht: WTrek = FTrekscos (0) = 80  20  1 = 1600 (J)
NB Let vooral op de regel bij WZ: de hoek tussen FZ en s is 95° (bedenk zelf waarom)
Stap 3: Tel alle verrichte arbeid bij elkaar op
Totale arbeid WOP = 0 - 300 - 1025 + 1600 = 275 (J)
Stap 4: Gebruik de Wet van Arbeid en Kinetische Energie.
WOP = ½ mveind² - ½ mvbegin²
275 = ½ 60 veind² - ½ 60  (2,0)²
275 = 30 veind² - 120
395 = 30 veind²
veind² = 13,1667
dus veind = 3,6 (m/s)
Stap 5: Controleer de eenheid, de grootte (kan het kloppen?) en de significante cijfers.
Gedaan (gegevens in 2 cijfers, redelijk getal in buurt van beginsnelheid).
Dus het antwoord is veind = 3,6 (m/s)
Tip: probeer zelf nog eens dit uit te rekenen met de stof van hoofdstuk 2 en 3 (eenparige versnelde beweging en
wetten van Newton) en zie het voordeel van deze methode.