Topologie in Rn

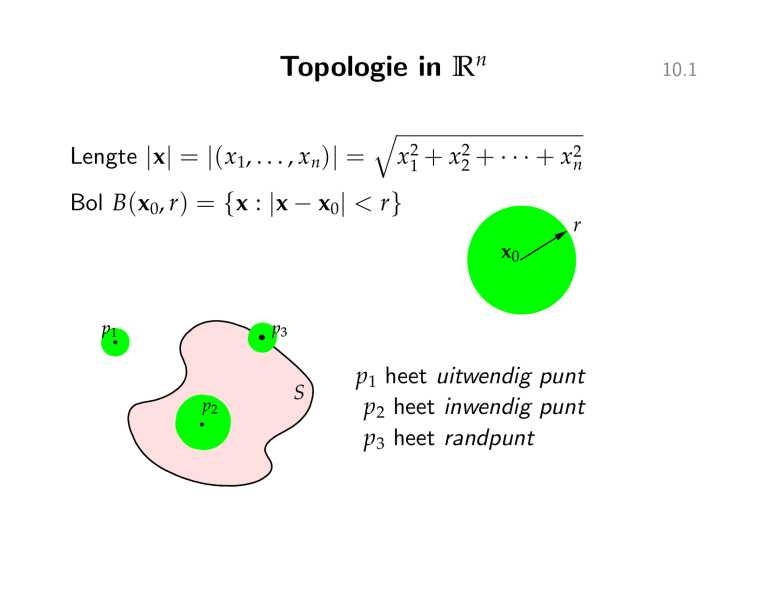
Topologie in Rn
Lengte |x| = |( x1, . . . , xn )| =
q
10.1
x12 + x22 + · · · + xn2
Bol B(x0, r ) = {x : |x − x0 | < r }
r
x0
p1
p3
p2
S
p1 heet uitwendig punt
p2 heet inwendig punt
p3 heet randpunt
p1
p3
p2
S
p1 heet uitwendig punt
p2 heet inwendig punt
p3 heet randpunt
• S heet open als elk punt in S inwendig is
⇐⇒ als S geen enkel randpunt bevat
• S heet gesloten als S alle randpunten bevat
• S open ⇐⇒ Rn \ S gesloten
Functies van meer variabelen
f
f ( x1 , . . . , x n )
( x1 , . . . , x n )
D ⊂ Rn
R⊂R
Domein D ⊂ Rn
Bereik R ⊂ R
Grafieken
12.1
n = 2 Grafiek van functie f ( x, y) is verzameling in R3:
( x, y, z) ∈ R : z = f ( x, y)
3
n = 3 Grafiek van functie f ( x, y, z) is verzameling in R4:
( x, y, z, w) ∈ R : w = f ( x, y, z)
4
Niveauverzamelingen
n = 2 Niveaulijn van functie f ( x, y) is kromme van punten
( x, y) met gelijke functiewaarden:
{ ( x, y) ∈ R2 : f ( x, y) = c }
1.5
1
0.15
0.5
0.1
0.05
-1.5
0
-1
y
-0.5
0
0
x
-0.05
-0.5
2
-0.1
1
-0.15
0
-2
-1
x
-1
0
1
2
-2
-1
y
-1.5
0.5
1
1.5
n = 3 Niveauvlak van functie f ( x, y, z) is oppervlak van
punten ( x, y, z) met gelijke functiewaarden:
{ ( x, y, z) ∈ R3 : f ( x, y, z) = c }
2
1.5
1
2
1.5
0.5
1
z
0
x
0.5
0 -2
-0.5
-1
0
-1
1
2
y
Limieten
12.2
lim f (x) = L:
x→y
(conceptueel)
x≈y


=⇒
f (x) ≈ L
x 6= y 
(definitie) Voor elke ε > 0 bestaat er δ > 0 zodat
x 6= y, |x − y| < δ
B(L, ε)
L
B(y, δ)
y
=⇒
| f (x) − L| < ε.
Limieten en continuiteit
Rekenregels:
lim( f + g) = lim f + lim g
lim f g = (lim f )(lim g)
f
lim f
lim =
g
lim g
Def
mits lim g 6= 0
Een functie f is continu in y als
lim f (x) = f (y).
x→y
Vuistregel Een formule is continu op zijn domein
x2 y
2
f ( x, y) = 2
,
continu
op
R
mits f (0, 0) = 0
2
x +y
1
0.5
0
-0.5
2
-1
-2
1
-1
x
0
0
y
-1
1
2
-2
xy
2
f ( x, y) = 2
,
continu
op
R
\ {0}
2
x +y
-2
-1
x
0
1
2
-2
-1
1
0
y
2
0.4
0.2
0
-0.2
-0.4
Partiële afgeleiden
y vast
f ( x + h, y) − f ( x, y)
f 1 ( x, y) = lim
h →0
h
x vast
f ( x, y + k) − f ( x, y)
f 2 ( x, y) = lim
k →0
k
∂f
Notatie: f 1 =
= D1 f = f x .
∂x
12.3
z
plane y = b
a, b, f (a, b)
z = f (x, y)
b
a
x
Figure 12-15
y
z
plane x = a
z = f (x, y)
a, b, f (a, b)
a
x
Figure 12-16
b
y
z
plane y = b
plane x = a
tangent plane
P
T2
T1
n
y
x
Figure 12-17
Kettingregel
12.5
Voorbeelden
1. f ( x, y), x = x (t), y = y(t)
0
0
d
f x ( t ), y ( t ) = f 1 x ( t ), y ( t ) x ( t ) + f 2 x ( t ), y ( t ) y ( t )
dt
∂ f dx ∂ f dy
df
=
+
.
dt
∂x dt ∂y dt
2. f (u, t), u = u(t)
0
d
f u ( t ), t = f 1 u ( t ), t u ( t ) + f 2 u ( t ), t
dt
df
∂ f du ∂ f
=
+
dt
∂u dt
∂t
Impliciet differentiëren
Voorbeeld
12.8
Beschouw de functie y( x ) die voldoet aan
2
2
x + y = 3,
y (1) =
√
2.
Wat is y0 (1)?
Uitwerking
Diff naar x:
Vul in x = 1:
2x + 2y( x )y0 ( x ) = 0
√
0
2 + 2 2 y (1) = 0
⇐⇒
0
y (1) =
1√
− 2 2.
Linearisatie, 1e-orde benaderingen
Def De linearisatie of 1e-orde benadering
van f ( x, y) in ( a, b) is
L(a,b) ( x, y) = f ( a, b) + f 1 ( a, b)( x − a) + f 2 ( a, b)(y − b)
Def f heet differentieerbaar in ( a, b) als f 1 en f 2 bestaan
in ( a, b), en
lim
( x,y)→( a,b)
f ( x, y) − L(a,b) ( x, y)
=0
|( x, y) − ( a, b)|
Stelling Laat f , f 1, en f 2 continu zijn in B ( a, b), r (voor
zekere r > 0). Dan is f differentieerbaar in ( a, b).
Gevolg Een formule f is differentieerbaar in elk inwendig punt
van D ( f ) ∩ D ( f 1 ) ∩ D ( f 2 )
Als f ( x, y) differentieerbaar is, dan is de vergelijking van het
raakvlak aan de grafiek van f in ( a, b) (grafiek ⊂ R3!)
z = L(a,b) ( x, y)
= f ( a, b) + f 1 ( a, b)( x − a) + f 2 ( a, b)(y − b)
of anders gezegd, het raakvlak A is de verzameling
n
A = ( x, y, z) ∈ R3 : z = f ( a, b) + f 1 ( a, b)( x − a) + f 2 ( a, b)(y − b)
Gelijkwaardig:
1. f ( x, y) is differentieerbaar in ( a, b)
2. het raakvlak in a, b, f ( a, b) is een ‘redelijke’ benadering
van de grafiek van f in ( a, b)
o
Gradiënt en richtingsafgeleide
Def
12.7
Gradiënt van f ( x, y)
∇ f ( x, y) = f 1 ( x, y), f 2 ( x, y) .
Def Directionele afgeleide in punt x = ( x, y) in richting
u = (u, v)
f (x + hu) − f (x)
Du f (x) = lim
h →0
h
f ( x + hu, y + hv) − f ( x, y)
= lim
h →0
h
Stelling
Du f ( x ) = ∇ f ( x ) · u
Let op!
D2u f = 2Du f , want
D2u f = ∇ f · (2u) = 2(∇ f · u) = 2Du f .
Meestal neem je aan |u| = 1.
Opmerkingen
• ∇ f ⊥ niveaulijn (-vlak) van f
• ∇ f is richting van sterkste stijging van f
• La (x) = f (a) + ∇ f · (x − a)
Hogere-orde afgeleiden
Notatie:
∂
f 12 ( x, y) =
∂y
Stelling
∂
f ( x, y)
∂x
Gegeven
• f , f 1, en f 2 continu op B(x0, r )
• f 12 en f 21 continu in x0
Dan is f 12 (x0 ) = f 21 (x0 )
2e-orde benaderingen
12.9
f ( x, y) ≈ f ( a, b) + f 1 ( a, b)( x − a) + f 2 ( a, b)(y − b)
1
+ f 11 ( a, b)( x − a)2 + f 12 ( a, b)( x − a)(y − b)
2
1
+ f 22 (y − b)2
2
Voorbeeld
Tentamen mei 2000
Gegeven is de functie f ( x, y) = x2 y2 + y.
a. Bepaal de vergelijking van het raakvlak aan de grafiek van
f in het punt (2, 1, 5).
b. In welke richting stijgt de functie f in het punt (2, 1) het
meest?
c. Geef de vergelijking van de niveaulijn van f door het punt
(2, 1) en bepaal de vergelijking van de raaklijn in het punt
(2, 1) aan deze niveaulijn.
Extreme waarden
Def
13.1
f heeft een globaal maximum in a ∈ D ( f ) als
f (x) ≤ f (a)
voor alle
x ∈ D ( f ).
f heeft een lokaal maximum in a ∈ D ( f ) als er een B(a, r )
bestaat zodat
D( f )
f (x) ≤ f (a)
voor alle x ∈ B(a, r ) ∩ D ( f ).
a
B(a, r )
B(b, r )
b
Stelling
Als f een lokale extreme waarde heeft in a, dan
óf
a is inwendig, f is differentieerbaar in a, en ∇ f (a) = 0
(stationair punt)
óf
a is inwendig en f is niet differentieerbaar in a
n=1:
óf
a ligt op de rand van D ( f )
n=1:
D( f )
Speciaal geval: inwendig punt, n = 2
Discriminant:
Stelling
∆ = f 12 (a)2 − f 11 (a) f 22 (a)
Gegeven a inwendig punt; ∇ f (a) = 0. Dan
∆<0
=⇒ extremum (min of max)
∆=0
=⇒ ?
∆>0
=⇒ zadelpunt
Als ∆ < 0,


>0
f 11 (a)

<0
=⇒ min
=⇒ max
Extrema op begrensde gebieden
13.2
Stelling
Als f continu is op een begrensde, gesloten
verzameling D, dan heeft f een globaal max en min op D.
Voorbeeld
Tentamen mei 2003
Bepaal het globale maximum en minimum van de functie
f ( x, y) = xy − y2 op het gebied D gegeven door x2 + y2 ≤ 1.
(Hint: gebruik voor de rand poolcoördinaten).
Dubbelintegralen
14.1
z = f (x)
f : D ⊂ R2 → R
ZZ
f (x) dA = V1 − V2
D
V1: volume boven xy-vlak
V2: volume onder xy-vlak
D
Eigenschappen
1. Als opp( D ) = 0 dan is
ZZ
f dA = 0 voor elke f
D
ZZ
2.
1 dA = opp( D )
D
ZZ
3.
ZZ
4.
( f + g) dA =
(λ f ) dA = λ
ZZ
ZZ
f dA +
ZZ
g dA
f dA voor elke λ ∈ R
Eigenschappen (2)
ZZ
5.
f dA =
ZZ
D
f dA +
ZZ
D1
f dA
D2
D2
D1
mits D = D1 ∪ D2 en D1 ∩ D2 = ∅
Z Z
ZZ
6. (driehoeksongelijkheid)
f dA ≤
| f | dA
7. f (x) ≤ g(x)
=⇒
ZZ
D
∀x ∈ D
f dA ≤
ZZ
D
=⇒
g dA
(monotonie)
Dubbelintegralen als herhaalde integralen 14.2
x = h1 (y)
y = g2 (x)
d
D
c
y = g1 (x)
a
Stelling
ZZ
D
x = h2 (y)
b
f is continu op D. Dan
f dA =
b Z g2 ( x )
Z
a
g1 ( x )
f ( x, y) dy dx =
d Z h2 ( y )
Z
c
h1 ( y )
f ( x, y) dx dy
Poolcoördinaten
⇐⇒
y = r sin θ
rdθ
dr
y
r
θ + dθ
θ
x
Oppervlakte-element
q
x 2 + y2
y
tan θ =
x
r=
x = r cos θ
14.4
dA = rdrdθ
Voorbeeld
Tentamen juli 2001
√
Het gebied G wordt gegeven door y ≥ x 3, y ≥ − x én
x2 + y2 ≤ 9. Bereken de integraal
x
ZZ
p
G
1 + ( x2 + y2 )3/2
dA.
Tripelintegralen
Voorbeeld van interpretatie:
R
vol(Ω) = ∆V
Ω
f ( x, y, z) is massadichtheid in ( x, y, z),
i.e. f ( x, y, z)∆V is massa van Ω
=⇒
RRR
f dV is totale massa van R
R
In rechthoekige coördinaten
dV = dxdydz
14.5
Herhaald integreren
z = h( x, y)
y
R
y = φ2 ( x )
D
a
z = g( x, y)
y = φ1 ( x )
y = φ1 ( x )
x
b
a
y = φ2 ( x )
( x, y)
x
b
x
D
ZZZ
R
f dV =
Z Z Z h( x,y)
D
f ( x, y, z) dz dxdy =
g( x,y)
=
b
Z
a
Z
φ2 ( x ) Z h( x,y)
φ1 ( x )
g( x,y)
f ( x, y, z) dzdydx
Cylindercoördinaten
q
x 2 + y2
y
tan θ =
x
z=z
r=
x = r cos θ
⇐⇒
y = r sin θ
14.6
z=z
z
P = (x, y, z)
= [r, θ, z]
d
z
O
x
θ
r
y
y
x
Integreren in cylindercoördinaten
z
r dθ
r
dr
d V = r dr dθ dz
dz
θ
x
Figure 14-39
dθ
y
Bolcoördinaten
ρ=
x = ρ sin φ cos θ
⇐⇒
y = ρ sin φ sin θ
14.6
q
x 2 + y2 + z2
φ = arccos(z/ρ)
y
tan θ =
x
z = ρ cos φ
z
P = (x, y, z)
= [ρ, φ, θ]
φ
ρ
φ
z
O
x
θ
r
y
y
x
Integreren in bolcoördinaten
z
ρ sin φ dθ
dρ
dθ
θ
ρ
[ρ,φ,θ ]
φ
dφ
ρ dφ
d V =ρ 2 sin φ dρ dφ dθ
y
x
Figure 14-44
Vectorfuncties van één variabele

 x (t)

r(t) =  y(t)

z(t)
11.1
r(b)





r(t)
v(t) = r0 (t)
r(a)
Snelheidsvector


0
x
 (t) 


v(t) := r0 (t) =  y0 (t) 


(snelheid v(t) = |v(t)|)
z0 (t)
Versnelling


00
x
 (t) 
 00

0
00
a(t) := v (t) = r (t) =  y (t) 


00
Parametriseringen
r(a) = r(b)
gesloten
(mogelijke zelfdoorsijding)
enkelvoudig gesloten
(geen zelfdoorsnijding)
Lengte
L=
b
Z
v(t) dt =
a
b
Z
|v(t)| dt
a
Booglengteparametrisering:
een parametrisering met v = |v| = 1;
te maken uit parametrisering r(t): s =
t
Z
v(t) dt.
a
11.2
Lijnintegralen
15.3
r(b)
C
ds
r(a)
Lengte(C ) =
Z
1 ds
C
Z
f (x) ds =
Lijnintegraal:
C
NB
b
Z
f r(t) |r0 (t)| dt
a
Integraal is onafhankelijk van keus van parametrisering
Vectorvelden
F(x) = F1 (x), F2 (x)
of
F(x) = F1 (x), F2 (x), F3 (x)
15.1
Veldlijnen
Def Een veldlijn
van F is een kromme r(t) waarvoor
r0 (t) k F r(t) .
Figure 15-3
‘Veldlijn is een kromme die bij het vectorveld past’
Conservatieve velden (R3)
15.2
Def
Als F(x) = ∇ ϕ(x) in gebied D, dan heet F
conservatief
F loodrecht op niveauvlakken van ϕ, { ϕ(x) = c}
(equipotentiaalvlakken)
Test
Als F conservatief, dan
• ∂y F1 = ∂ x F2
• ∂z F2 = ∂y F3
(∇ × F = 0)
• ∂ x F3 = ∂z F1
NB Alléén =⇒ : Test kan uitsluiten dat F conservatief
is, maar niet bewijzen!
Lijnintegralen van vectorvelden
r(b)
Arbeid
W = F · r(b) − r( a)
r(a)
θ
15.4
= |F| |r(b) − r( a)| cos θ
F
Langs stukje C :
F
T̂
ds
C
T̂ is eenheidsraakvector langs C ; T̂ = 1
(bv T(t) = r0 (t), T̂ = T/ |T|)
Afgelegde weg:
T̂ ds
Arbeid over stukje ds:
Arbeid over C :
Z
C
F · T̂ ds
F · T̂ ds
Berekening
Z
r0 (t) 0
F · T̂ ds =
F r(t) · 0
|r (t)| dt
|r (t)|
C
a
Z b
0
=
F r(t) · r (t) dt
b
Z
a
Vergelijk:
Scalaire functie f :
Z
Z C
Vectorfunctie F:
C
f ds =
b
Z
F · T̂ ds =
a
f r(t) |r0 (t)| dt
b
Z
a
F r(t) · r0 (t) dt
Opmerkingen
1. Notatie:
Z
C
F · T̂ ds =
Z
C
F · dr.
2. Oriëntatie:
andersom doorlopen ⇐⇒ integraal verandert van teken
(alléén bij integralen van vectorfuncties!)
3. Gesloten kromme:
C2
B
Z
C
A
C1
C
F · dr =
Z
C1
F · dr −
Z
C2
F · dr
Integralen van conservatieve vectorvelden
1. Als F conservatief (F = ∇φ) dan
Z
C
F · dr = φ r(b) − φ r( a)
Integraal hangt alleen af van begin- en eindpunt!
2. Als C gesloten is, dan is
Z
C
F · dr = 0.
Stelling
Gebied D is samenhangend. Equivalent:
1. F is conservatief
Z
2.
C
Z
3.
C
F · dr = 0 voor elke gesloten C in D
F · dr hangt alleen af van begin- en eindpunt van C
Oppervlakte-integralen
15.5
z
v
d
Ë
(u, v)
r(u, v)
R
c
a
u
b
y
x
Figure 15-16
∂r
dv
∂v
r0
dS
∂r
du
∂u
r(u 0 , v)
r(u, v0 )
r(u 0 + du, v)
r(u, v0 + dv)
Figure 15-20
dS = |ru du × rv dv| = |ru × rv | dudv
ZZ
S
f dS =
ZZ
D
f r(u, v) |ru × rv | dudv
Speciaal geval
S is grafiek {z = f ( x, y)}
r( x, y) = x, y, f ( x, y)
r x = (1, 0, f x )
en
voor
( x, y) ∈ D
ry = (0, 1, f y )
r x × ry = (− f x , − f y, 1)
dS =
ZZ
S
q
1 + f x2 + f y2 dxdy
g( x, y, z) dS =
ZZ
D
g x, y, f ( x, y)
q
1 + f x2 + f y2 dxdy
Oppervlakte-integralen van vectorvelden
v · N̂ dS
Flux door oppervlak:
z
N̂
v dt
θ
dS
P
Ë
y
x
Figure 15-29
15.6
Def
Oppervlak S heet oriënteerbaar als er een continu
eenheidsnormaalvectorveld N̂ bestaat op S
z
N̂
N̂
P
N̂
y
x
Figure 15-27
Figure 15-28
ru × rv
±
goede kandidaat voor N̂
|ru × rv |
Berekening
I=
ZZ
F · N̂ dS
S
=±
ZZ
D
=±
ZZ
ru × rv
F r(u, v) ·
|ru × rv | dudv
|ru × rv |
F r(u, v) · ru × rv dudv
D
ZZ
Notatie:
S
F · N̂ dS =
ZZ
S
F · dS.
n=2
scalaire f
vector F
1d: C
f ds = f (r) |r0 | dt
F · dr = F(r) · r0 dt
2d: D
f dV
div F dV
n=3
scalaire f
vector F
1d: C
f ds = f (r) |r0 | dt
F · dr = F(r) · r0 dt
2d: S
f dS = f (r) |ru × rv | dudv
F · dS = ±F(r) · ru × rv dudv
3d: D
f dV
div F dV
Grad-div-rot
16.1
Gradient
∇ f = grad f = ( f x , f y, f z )
Interpretatie: richting van sterkste stijging van f
Divergentie
div F = ∂ x F1 + ∂y F2 + ∂z F3
Interpretatie: verandering van grootte van een meegevoerd
volume


 ∂z F2 − ∂y F3 


Rotatie
rot F = curl F =  ∂ x F3 − ∂z F1 


∂y F1 − ∂ x F2
Interpretatie: moment uitgeoefend door krachtenveld