Scientific abstract

Populaire Samenvatting
In de kwantumfysica, de theorie die interacties tussen de kleinste deeltjes beschrijft, hebben deeltjes geen absolute plaats maar hebben ze een bepaalde distributie
gekregen over de ruimte. Dat wil dus zeggen dat je waar je ook meet, altijd een
bepaalde kans hebt om het deeltje tegen te komen. Op bepaalde plaatsen in
de ruimte is de waarschijnlijkheid natuurlijk groter dan andere plaatsen van de
ruimte, en op bepaalde plaatsen is de kans ook compleet verwaarloosbaar. Deze
waarschijnlijkheden ’bestaan’ alleen voordat je daadwerkelijk gaat meten waar
een dergelijk deeltje zich bevindt, als je eenmaal gaat meten waar een deeltje
zich bevindt, dan hef je de onzekerheid op. Het punt waar het dus hier om
gaat is het gegeven dat een deeltje geen gedefinieerde plaats in de ruimte heeft
voordat je eraan gaat meten.
Er zijn zo ook configuraties bedenkbaar waarbij de waarschijnlijkheid van het
deeltje richting een barrière reist (dit kan van alles zijn, we nemen voor het
gemak een muur) en het verassende hierbij is dat het deeltje in de kwantummechanica door de barrière heen kan gaan. Als een deeltje door een barrière heen
reist heet dit tunnelen. Dit tunnelen komt doordat in de kwantummechanica de
positie van deeltjes wordt gerepresenteerd door een golffunctie. Zo’n golffunctie
geeft de waarschijnlijkheid van een deeltje als functie van de plaats en de tijd.
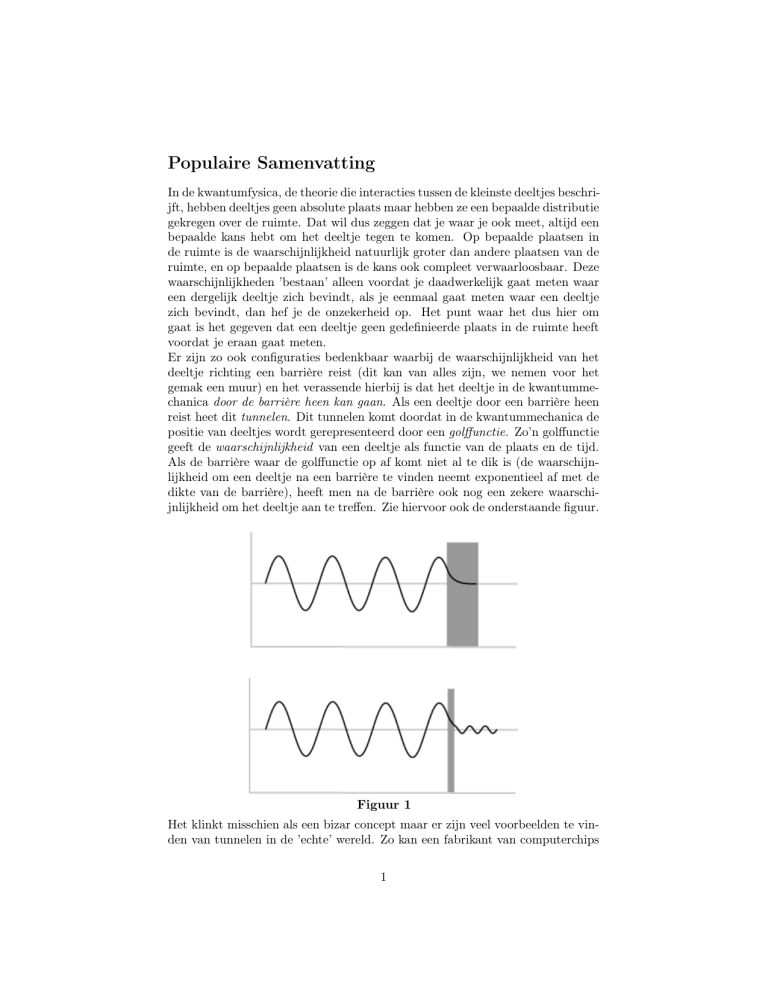
Als de barrière waar de golffunctie op af komt niet al te dik is (de waarschijnlijkheid om een deeltje na een barrière te vinden neemt exponentieel af met de
dikte van de barrière), heeft men na de barrière ook nog een zekere waarschijnlijkheid om het deeltje aan te treffen. Zie hiervoor ook de onderstaande figuur.
Figuur 1
Het klinkt misschien als een bizar concept maar er zijn veel voorbeelden te vinden van tunnelen in de ’echte’ wereld. Zo kan een fabrikant van computerchips
1
de banen in een computerchip die de elektrische signalen voort geleiden niet te
dicht op elkaar leggen omdat er anders elektronen van de ene baan naar de andere baan tunnelen. Een effect wat natuurlijk absoluut niet wenselijk is, omdat
dan je signalen in de knoop raken.
In dit bachelorproject gaan we kijken naar een ander soort barrière, namelijk
een barrière opgeworpen door het elektrische potentiële veld. Men kan zich
voorstellen dat als de energie van het veld hoog genoeg is dat het op gegeven
moment op een bepaalde afstand van een gegeven punt genoeg energie heeft
gekregen om twee deeltjes te laten ontstaan (massa is tenslotte niks meer dan
een alternatieve vorm van energie). Volgens de wet van ladingsbehoud moet er
dan een deeltje en het bijbehorende antideeltje ontstaan. Het effect waarbij dit
gebeurt heet het Schwinger Effect en is hetgeen wat wij in dit verslag hebben
nagerekend. De methode die wij hiervoor gebruikt hebben bewandelt een ander
pad dan hoe het effect in eerste instantie in 1951 door Nobelprijswinnaar Julian
Schwinger is berekend. Om de waarschijnlijkheid van dit effect te berekenen
wordt er namelijk gebruik gemaakt van instantonen, theoretische deeltjes die
geen gezette plaats in de tijd hebben maar gelokaliseerd zijn in de tijd.
Men kan de berekening dan als volgt voorstellen. Stel dat een deeltje zich voortbeweegt in een sterk homogeen elektrisch veld. Op de afstand waarop normaal
het deeltje van te voren zou zijn gekomen komt het deeltje de barrière tegen waar
het doorheen moet tunnelen. De dikte van de barrière wordt gedefinieerd door
de energie die het veld moet verrichten als deze energie gelijk is aan twee maal
de rustmassa van het te verschijnen deeltje (het deeltje met zijn antideeltje). In
dit project toon ik aan dat deze berekening equivalent is aan de berekening van
Schwinger.
2