Redeneren en Bewijzen

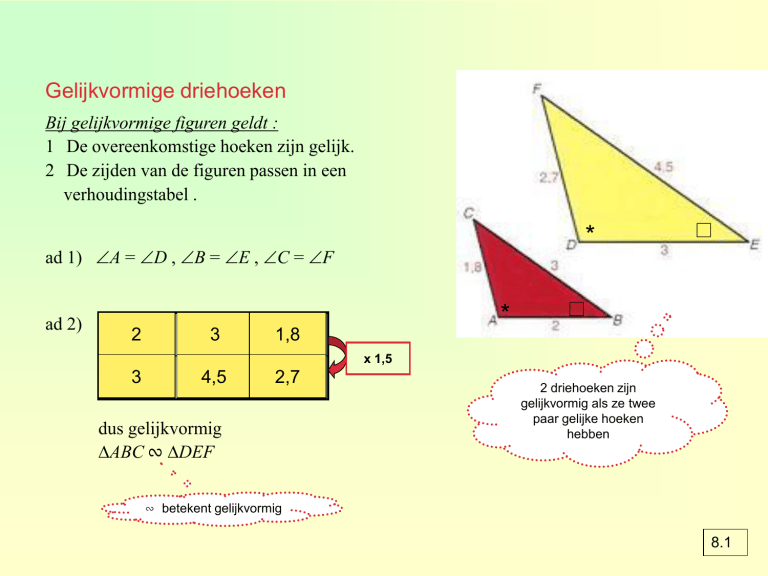
Gelijkvormige driehoeken
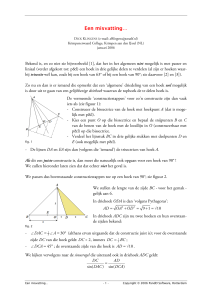
Bij gelijkvormige figuren geldt :
1 De overeenkomstige hoeken zijn gelijk.
2 De zijden van de figuren passen in een
verhoudingstabel .
*
ad 1) A = D , B = E , C = F
ad 2)
2
AB
3
BC
*
1,8
AC
□
□
x 1,5
3
DE
4,5
EF
2,7
DF
dus gelijkvormig
∆ABC ∾ ∆DEF
2 driehoeken zijn
gelijkvormig als ze twee
paar gelijke hoeken
hebben
∾ betekent gelijkvormig
8.1
Hoe herken je gelijke hoeken ?
Bij snijdende lijnen zijn
overstaande hoeken gelijk.
Bij evenwijdige lijnen horen
gelijke Z-hoeken.
*
Bij evenwijdige lijnen horen
gelijke F-hoeken.
□
□ □
*
□
8.1
Snavel- en zandloperfiguren
snavelfiguur
zandloperfiguur
∆ABC ∾ ∆DBE
∆KLM ∾ ∆ONM
A = D
B = B
C = E
C
E
K
L
K = O
L = N
M = M
B
M
D
A
AB
DB
N
BC
BE
AC
DE
KL
ON
O
LM KM
NM OM
8.1
Congruente driehoeken
Als 2 driehoeken gelijkvormig EN even groot zijn dan zijn de driehoeken congruent.
8.1
De meeste opgaven zijn makkelijk te tekenen in
programma’s als Cabri en Geogebra.
• Geogebra is gratis te downloaden.
• Werkt onder Windows, Linux en Mac.
• Heeft een gunstige learn to use en use to learn
verhouding.
• Is Nederlandtalig ondersteund.
• Wordt in de methode en door de docenten
gebruikt.
Opgave overzicht 1
•
•
•
•
•
•
Opgave 3
Opgave 4
Opgave 5
Opgave 6
Opgave 7
Opgave 10
opgave 11
Toon aan dat AN = BN
Teken MA en MB
MA = MB (straal cirkel)
MN = MN
ANM = BNM = 90°
A
N
∆ANM ≌ ∆BNM
(ZZR)
dus AN = BN
B
∙
M
Definities
Een definitie is een afspraak.
Definitie van gelijkbenige driehoek :
Een gelijkbenige driehoek is een driehoek met 2 gelijke zijden.
Definitie van gestrekte hoek :
Een gestrekte hoek is een hoek van 180°.
Definitie van parallellogram :
Een parallellogram is een vierhoek waarvan beide paren
overstaande zijden evenwijdig zijn.
Definitie van ruit :
Een ruit is een vierhoek met vier gelijke zijden.
8.2
Stellingen
Een stelling is een eigenschap of bewering die te bewijzen is.
Stelling gelijkbenige driehoek :
Als in een driehoek twee zijden gelijk zijn, dan zijn de
tegenoverliggende hoeken ook gelijk.
Als in een driehoek twee hoeken gelijk zijn, dan zijn de
tegenoverliggende zijden ook gelijk.
Stelling van overstaande hoeken :
De overstaande hoeken bij twee snijdende lijnen zijn gelijk.
Stelling van hoekensom driehoek :
De som van de hoeken van een driehoek is 180°.
8.2
Werkschema : het bewijzen van een stelling
1 Formuleer wat gegeven is voor een concrete situatie.
2 Noteer wat bewezen moet worden voor de gekozen situatie.
3 Geef het bewijs. Vermeld hierbij de definities en stellingen die je gebruikt.
8.2
Definitie van middelloodlijn:
A
De middelloodlijn van een lijnstuk
is de lijn door het midden van dat
lijnstuk die loodrecht op dat lijnstuk
staat.
∙
∙B
Definitie van bissectrice:
De bissectrice van een hoek is de
lijn die de hoek middendoor deelt.
∙
∙
A
∙
∙ ∙
8.2
opgave 28
a BAS = ½A = 30°
cos 30° =
AS =
5
AS
5
1
10
10
5
3 10 3


3 3



cos 30 1 3
3
3
3
3
3
2
b cos 30° = 1 3
2
1
3
AS
10
3

3

7
21
AC
3
cos 30° ≠
AS
AC
dus ASC ≠ 90°
Definitie van hoogtelijn:
C
D
Een hoogtelijn in een driehoek is
de loodlijn vanuit een hoekpunt
op de overstaande zijde.
B
A
C
Definitie van zwaartelijn:
Een zwaartelijn in een driehoek is
de lijn die gaat door een hoekpunt
en het midden van de overstaande zijde.
M
A
B
8.2
opgave 31
Teken EF loodrecht op AB
In ∆BCD is BD = CD = 6
∆BCD is een vergroting van ∆BEF met factor 2
dus EF = ½CD = 3
en BF = ½BD = 3
DF = BD – BF = 6 – 3 = 3
CD
AD
6
3
AD
6
AD 
3
In ∆ADC is tan 60° =
AF = AD + DF 
6
3
3
F
6
3
3
EF

dus EAB ≈ 25°
tan EAB = tan EAF =
6
AF
3
3
3
Middelloodlijnen in een driehoek
In een driehoek gaan de 3
middelloodlijnen door één punt.
Dat punt is het middelpunt van
de omgeschreven cirkel van de
driehoek.
C
M
A
|
|
B
8.3
Zwaartelijnen in een driehoek
De drie zwaartelijnen van een driehoek
gaan door één punt, het zwaartepunt.
En verdelen elkaar in stukken die
zich verhouden als 2 : 1.
C
E
Z
(1)
D
(2)
A
|
F
|
B
8.3
Hoogtelijnen in een driehoek
De drie hoogtelijnen van een
driehoek gaan door één punt.
C
D
E
A
F
B
8.3
Bissectrices in een driehoek
In een driehoek gaan de drie
bissectrices door één punt.
Dat punt is het middelpunt van
de ingeschreven cirkel van de
driehoek.
C
x x
M
A
°
°
∙
∙
B
8.3
Koordenvierhoeken
Een koordenvierhoek is een vierhoek waarvan
de hoekpunten op één cirkel liggen.
D
Koordenvierhoekstelling :
Als ABCD een koordenvierhoek is, dan is de
som van elk paar overstaande hoeken 180°.
Omgekeerde koordenvierhoekstelling :
Als in een vierhoek de som van een paar
overstaande hoeken 180° is, dan is de
vierhoek een koordenvierhoek.
C
M
∙
B
A
8.3
opgave 50
Gegeven :
Driehoek ABC en het snijpunt M van de
middelloodlijnen van de zijden.
C
Te bewijzen :
M is het middelpunt van de omgeschreven
cirkel van driehoek ABC,
ofwel AM = BM = CM.
Bewijs :
M ligt op de middelloodlijn van AB
dus AM = BM
M ligt op de middelloodlijn van BC
dus BM = CM
M
A
|
|
B
AM = BM = CM
Dus M is het middelpunt van de omgeschreven
cirkel van driehoek ABC.
8.4
opgave 54
C
P
v
Q
v
D
E
A
Op dezelfde manier vind je dat BE de middelloodlijn
is van PR en dat AD de middelloodlijn is van QR.
De hoogtelijnen van ∆ABC zijn dus de middelloodlijnen van ∆PQR.
De middelloodlijnen van ∆PQR gaan door één punt dus de
hoogtelijnen van ∆ABC gaan door één punt.
v
a Teken ∆ABC
Teken parallellogram ABPC, ABCQ
en ARBC
b CF staat loodrecht op AB
PQ // AB (parallellogram) 
 CF staat loodrecht op PQ

CQ = AB
 CQ = CP
CP = AB
 CF is de middelloodlijn van PQ
B
F
R
Opgave 55b De stelling van Thales
Gegeven :
Driehoek ABC en M het middelpunt van de
cirkel en midden van AB.
A
C
1
2
Te bewijzen :
Hoek ACB = 90 graden.
Bewijs :
AM = BM
BM = CM
AM = CM
M
want AM=BM=CM= r
Dus
Hoek MAC=MCA. En hoek MBC=MCB
Hoek A + hoek B + Hoek C 1,2 =180
Hoek C1+ hoek C2 + Hoek C 1,2 = 2 hoek C1,2
2 hoek C1,2=180
Hoek ACB = 90 graden
B
Koordenvierhoeken
180- (hoek A1 +hoek D1) = hoek M1
180- (hoek C1 +hoek D2) = hoek M2
180- (hoek B1 +hoek C2) = hoek M3
180- (hoek A2 +hoek B2) = hoek M4
D
1
2
C
1
2
2
1
180- 2 x hoek A1 = hoek M1
180- 2 x hoek C1 = hoek M2
180- 2 x hoek C2 = hoek M3
180- 2 x hoek A2 = hoek M4
∙
M
3
4
2
1
1
2
B
A
720- 2x hoek A + 2 x hoek C = 360
2x hoek A + 2 x hoek C = 360
hoek A + hoek C = 180
8.3
C
Opgave 57b
D
1
2
2
1
1
1
A
hoek A1,2 =hoek D1
hoek C2 = hoek D2
hoek C1 =hoek B1,2
hoek B2 =hoek A2
2
∙
2
B
M
+
hoek A1,2 + hoek C2 + hoek C1 - hoek A2 = hoek D1 + hoek D2 + hoek B1,2 - hoek B2
hoek A1 + hoek C = hoek B1 + hoek D
hoek A1 + hoek C + hoek B1 + hoek D = 360
hoek A1 + hoek C = 180
8.3
opgave 59
Gegeven :
Twee cirkels met snijpunten A en B,
F
de lijn k door A snijdt de cirkels ook nog in C en D
B
en de lijn l door B snijdt de cirkels ook nog in E en F.
2 1x
Te bewijzen :
CF // DE
1x
Bewijs :
A
Teken CF, AB en DE.
C
C1 + B2 = 180° (koordenvierhoekstelling)
C1 = B1
B1 + B2 = 180° (gestrekte hoek)
C1 = D1
B1 + D2 = 180° (koordenvierhoekstelling)
D1 = B1
D1 + D2 = 180° (gestrekte hoek)
dus CF // DE (F-hoeken)
E
l
2 1x
D
k
Opgave overzicht met hints of uitwerkingen.
•
•
•
•
•
•
•
•
•
•
•
Opgave 62
Opgave 63
Opgave DT6
Opgave DT 7a
Opgave DT 7b
Opgave DT 8
Opgave DT 14
Opgave DT 15
Opgave GO 41
Opgave GO 42
Opgave GO 43
•
•
•
•
•
•
•
•
•
•
•
Opgave GO 45
Opgave GO 47
Opgave GO 48
Opgave GO 49
Extra1
Extra2
Extra3
Extra4
Extra5
Extra6
Brandpunt