Uitwerkingen Herhalingsopgaven SE 2 Elektrische en Magnetische

Uitwerkingen Herhalingsopgaven SE 2 Elektrische en Magnetische Velden V6 NAT
Elektrische Velden
1)

 Fe
a) Elektrische Veldsterkte = Elektrische kracht op een Coulomb positieve lading ( E 
)
q
b) Eenheid: N/ C of V/m.
c) Een elektrisch veld waarbij de veldsterkte overal gelijk (en gelijkgericht) is.
d) Het elektrisch veld tussen twee (lange) condensatorplaten is homogeen.
V
J /C
Nm
N
e) 1  1
1
1
m
m
Cm
C
2)
a) Hulplijnen die de richting van de elektrische veldsterkte aangeven.
b) * ze snijden elkaar nooit
* ze gaan van positieve naar negatieve lading
* ze staan loodrecht op een geladen geleider
* de veldlijnendichtheid geeft de grootte van het elektrisch veld aan
* de raaklijn aan de veldlijn geeft de richting van het elektrisch veld aan
* binnen in een geleider zijn er geen elektrische veldlijnen
c) Anders zouden op het oppervlak van de geleider ladingen onder invloed van deze veldsterkte gaan
rondlopen.
d) Veldlijnen staan op gelijke afstand en in de zelfde richting.
e) Omdat binnen een geleider (het metaal van de auto) er geen elektrisch veld is.
3)
a) Het negatief geladen bolletje ondervindt een elektrische kracht naar links, dus is aan de linkerkant van de
tekening een positief geladen voorwerp. Veldlijnen lopen van positief naar negatief, dus in dit geval van links
naar rechts.
b) Zie tekening: tan 40° = Fe / Fz dus Fe = Fz tan 40° dus q E = m g tan 40°
40
Fe
Fz
4)
o
Ofwel: 30.10-9 E = 20.10-6 . 9,81 . tan 40°. Dit levert E = 5487,7 = 5,5.103 (N/C)
Let op: massa moet in (kg) worden ingevuld dus 20 (mg) = 20 .10-6 (kg)
c) Nu tan  = Fe / Fz = qE / mg = 30.10-9 . 3000 / 20.10-6 . 9,81 = 0,4587 dus  = 25°
a) Elektrische potentiaal is de elektrische energie van een Coulomb positieve lading ( V 
Eel
)
q
b) Langs de elektrische veldlijn neemt de potentiaal af.
c) We (A B) = q (VA – VB)
d) Eel = q V = -1,6.10-19 . 10 = -1,6.10-18 (J)
5)
a) Fz = mg = 9,1.10-31 . 9,81 = 8,9.10-30 (N) en Fe = qE = 1,6.10-19 . 400 = 6,4.10-14 (N) dus Fz  Fe
b) Veldlijnen gaan in de richting van de dalende potentiaal dus van B naar A.
c) Het elektron ondervindt een kracht tegengesteld aan de veldlijnen, omdat het negatief is, dus wordt het
versneld van A naar B (want de veldlijnen gaan van B naar A)
d) Eel,A = qVA = -1,6.10-19 . 15 = -2,4.10-18 (J) en Eel,B = qVB = -1,6.10-19 . 45 = -7,2.10-18 (J)
e) De arbeid van de elektrische kracht is: q(VA – VB) = -1,6.10-19 . (15 – 45) = 4,8.10-18 (J)
6)
a) E  
V
dV
(eigenlijk: E  
)
x
dx
X2
b) de oppervlakte onder de grafiek tussen de twee waarden voor x. Wiskundig V 
 E  dx
X1
c) de helling van de raaklijn bij waarde x. Wiskundig E  
dV
dx
7)
a) E  
V
0  VA

 2500 dus VA = 125 (V)
x
0,05
b)
c) VP – VB = E x dus VP – 0 = 2500 . 0,035 = 87,5 (V) dus VP = 88 (V)
d) We (P B) = q (VP – VB) = -2,0.10-9 (87,5 – 0) = -1,8.10-7 (J)
8)
a) Het bolletje ondervindt een elektrische kracht in de richting van de veldlijnen, dus is positief.
b) tan 70° = Fz / Fe dus Fe = Fz tan 70° invullen levert:
q E = m g / tan 70°
q . 800 = 5,6.10-6 . 9,81/ tan 70° dus q = 2,5.10-8 (C)
c) De resulterende kracht verandert niet (homogeen veld dus Fe constant en Fz ook constant) en als de
resulterende kracht constant is dan volgt uit a = F / m dat de versnelling dat ook is. Dus de beweging is
eenparig versneld.
d) VA – VB = E x = 800 . 0,044 . cos 70° = 12 (V) dus VB = VA – 12 = 36 – 12 = 24 (V)
e) Fres = √(Fe² + Fz²) = 5,85.10-5 (N) dus a = F / m = 10,44 (m/s²)
met s = ½ a t² volgt dat 0,044 = ½ 10,44 t² dus t = 0,09181 (s) dus v = at = 0,96 (m/s)
Anders: ½ mv² = q(VA-VB) + mgh ook v = 0,96 (m/s) [NB: zwaarte-energie niet te verwaarlozen]
f) ½ mv² = ½ . 5,6.10-6 . 0,96² = 2,6.10-6 (J)
9)
a) Fe = Fz dus q E = mg en met E = - V / x volgt E = 3200 (V/m) naar beneden
dus q . 3200 = 3,0.10-6 . 9,81 dus q = 9,2.10-9 (C)
maar wordt aangetrokken door de plusplaat dus is negatief: q = - 9,2 (nC)
b) VP – VB = E x = 3200. 0,015 = 48 (V) en VB = 0 dus VP = 48 (V).
EP = q VP = -9,2.10-9 . 48 = -4,4.10-7 (J)
c) Nu geldt E = 30 / 0,025 = 1200 (V/m) dus Fe = q E = 9,2.10-9 . 1200 = 1,104.10-5 (N)
Fz blijft gelijk dus Fz = 2,94.10-5 (N) dus Fnetto = Fz – Fe = 1,84.10-5 (N)
met F = m a volgt dan a = 1,84.10-5 / 3,0.10-6 = 6,13 = 6,1 (m/s²)
d) s = ½ at² dus 0,015 = ½ 6,13. t² dus t = 0,070 (s) en v = at = 0,43 (m/s)
e) Nu VP is niet meer 48 (V) maar: VP – VB = 1200 . 0,015 = 18 (V) dus VP = 18 (V) want VB = 0 (V)
We (P →B) = q (VP – VB) = -9,2.10-9 (18 – 0) = - 1,7.10-7 (J)
10)
a) 1 (eV) is de energie die een elektron krijgt bij het doorlopen van 1 (V) potentiaalverschil.
b) 3,2 (eV) = 3,2 . 1,6.10-19 = 5,12.10-19 (J)
c) 6,7.10-18 (J) = 6,7.10-18 / 1,6.10-19 = 42 (eV)
11)
a) Ek = 450 (eV) = 7,2.10-17 (J) dus ½ mv² = 7,2.10-17 en m = 9,1.10-31 (kg) levert v = 1,26.107 (m/s)
b) 1 (A) = 1 (C/s) dus 1,0.10-6 (C/s) / 1,6.10-19 (C/e) = 6,25.1012 (e/s)
12)
a) Ek = ½ mv² = ½ 9,1.10-31 . (6,0.106)² = 1,638.10-17 (J) = 102,38 (eV) = 102 (eV)
b) Elektron wordt versneld naar B dus B is positief en A negatief, de veldlijnen lopen dus van B naar A: dus
VB-VA = E x = 2,5.103 . 0,04 = 100 (V). VB = 0 (V) dus VA = 0 – 100 = -100 (V)
c) Eel = q VA = -1,6.10-19 . –100 = 1,6.10-17 (J) (=100 eV)
d) Ek = 100 (eV) + 102 (eV) = 202 (eV) = 3,23.10-17 (J)
e) Ek = ½ mv² dus v = 8,4.106 (m/s)
13)
a) Fe = q E = q V / d = 1,6.10-19 . 40 / 0,02 = 3,2.10-16 (N)
b) In horizontale richting: x = v t dus t = x / v = 0,06 / 2,0 .107 = 3,0.10-9 (s)
In verticale richting: a = Fe / m = 3,2.10-16 / 9,1.10-31 = 3,52.1014 (m/s²)
Dus y = ½ a t² = ½ 3,52.1014 . (3,0.10-9)² = 1,6.10-3 (m) = 1,6 (mm)
c) Verticaal: vy = a t = 3,52.1014 . 3,0.10-9 = 1,05.106 (m/s)
Met Pythagoras volgt dan: v = √(vx2 + vy2)= 2,0.107 (m/s) en tan  = vy/vx dus  = 3°
Magnetische Velden
14)
a) Verschijnsel dat een stof magnetisch wordt als er een magneet bij wordt gehouden.
b) Stoffen die magnetisch te maken zijn: ijzer, nikkel en kobalt.
c) * gaan van noord- naar zuidpool
* snijden elkaar nooit
* zijn altijd gesloten krommen
* veldlijnendichtheid geeft de grootte van de magnetische inductie aan
* raaklijn geeft de richting van de magnetische inductie aan.
d) 1 (T) is de magnetische inductie waarbij op een stroomdraad van 1 (m) lang waardoor een stroom loopt van
1 (A) een lorentzkracht wordt uitgeoefend van 1 (N), dus 1 (T) = 1 (N/Am) (volgt uit F L = B I l sin )
15)
a) Met behulp van de rechterhandregel voor een stroomdraad volgt:
b) Met behulp van de rechterhandregel voor een stroomspoel volgt:
16)
a) B = 0 NI / l met N aantal windingen, I de stroomsterkte door de spoel en l de lengte van de spoel.
b) uit de formule volgt: 0 = Bl / NI dus voor eenheden:
[0] = T m / A = (N/Am) m / A = N / A² = (kg m) / (s² A²)
c) B = 0 NI / l = 4.10-7 1000 . 2,0 / 0,01 = 0,25 (T)
17)
a) B = 0 NI / l = 4.10-7 1000 . 1,3 / 0,25 = 6,5.10-3 (T)
b) De stroomrichting is van de plus- naar de minpool van de spanningsbron, met de rechterhandregel voor een
stroomspoel volgt dan dat de veldlijnen in de spoel van rechts naar links lopen. Dat wil zeggen dat ze aan de
linkerkant van de spoel eruit komen, dus dat daar de noordpool van de spoel zit.
c) De veldlijnen ter plekke van de stroomdraad lopen naar links, de stroomsterkte is omhooggericht. Dat levert
met de linkerhandregel dat de lorentzkracht het papier uit is.
18)
a) De noordpool zit aan de rechterkant van de spoel (de veldlijnen komen rechts eruit)
b) Met behulp van de rechterhandregel volgt dat de stroomrichting door de spoel van A naar B is dus de
potentiaal van A is hoger dan de potentiaal van B.
c) B = 0 NI / l = 4.10-7 1200 . 0,050 / 0,25 = 3,0.10-4 (T)
d) De magnetische veldlijnen lopen van links naar rechts, de stroom door de draad naar beneden, dus met
behulp van de linkerhandregel volgt dan dat de lorentzkracht het papier uit gericht is.
19)
a) FZ loodrecht naar beneden = m g = 0,010.9,81 = 0,0981 (N)
FL horizontaal naar links gericht (loodrecht op verticale veldlijnen! en de snelheid is constant)
FN loodrecht op het vlak van tekening omhoog
Grootte van FL en FN volgt uit het feit dat de krachten evenwijdig aan het vlak en loodrecht erop in
evenwicht moeten zijn: Dus FN = FL┴ + FZ┴ en FL// = FZ//
b) FL moet naar links gericht zijn en het B-veld omlaag. Met behulp van de linkerhandregel volgt dan dat de
stroom van P naar Q moet lopen door het staafje. Dus L is verbonden met de pluspool van de batterij.
c) FL// = FZ// = FZ sin 25° = 0,0981.sin25° = 4,146.10-2 (N)
Dus FL = FL// / cos 25° = 4,56.10-2 (N) = B I l sin 90° = 0,050 . I . 0,10 dus I = 9,1 (A)
d) Dan FZ// en FL// zelfde kant op en evengroot dus Fres = 2 FZ// = 2.4,146.10-2 = 8,292.10-2 (N)
Dus a = Fres / m = 8,292.10-2 / 0,010 = 8,3 (m/s²) langs de helling omlaag.
20)
In een luidspreker zit een stroomspoel om een permanente ringmagneet. Als de stroom door de stroomspoel
wordt gevoerd, dan ondervindt deze spoel een lorentzkracht naar binnen of naar buiten gericht. Aan de
stroomspoel zit de conus bevestigd, die dus met de spoel naar binnen of buiten beweegt. Door de
stroomrichting in de spoel te laten wisselen (wisselstroom) draait ook de lorentzkracht van richting om en
daarmee de bewegingsrichting van de spoel.
21)
a) Door stroom door een spoel te sturen die zich in een magneetveld bevindt werkt er een lorentkrachtkoppel
op die spoel, die de spoel laat draaien.
b) Als dat niet zou gebeuren, dan zou de spoel na een halve slag een koppel tegengesteld aan de
bewegingsrichting krijgen en zou de motorbeweging omdraaien.
c) Dat gebeurt met behulp van collectorborstels: steeds de andere kant van de spoel is verbonden met de
positieve pool van de spanningsbron.
22)
a) EK = 240 (eV) = 240.1,6.10-19 = 3,84.10-17 (J) = ½ mv² dus v = 9,187.106 = 9,19.106 (m/s)
b) De stroomrichting is tegengesteld aan de snelheid van het elektron, dus naar links. Het veld is het papier in,
dus de lorentzkracht is volgens de linkerhandregel omlaag gericht. Het elektron zal dus naar beneden afbuigen.
c) uit FL = FMPZ ofwel Bqv = mv² / r volgt r = mv / Bq dus r = 9,1.10-31 . 9,187.106 / 0,50.10-3 . 1,6.10-19 = 0,1045
(m) dus diameter = 2 r = 0,21 (m).
d) die tijd is gelijk aan ½ T en met v = 2r / T volgt: T = 2r / v = 2  0,1045 / 9,187.106 = 7,15.10-8 (s) dus de
gevraagde tijd is ½ T = 3,6.10-8 (s) (NB: aangezien FL steeds loodrecht staat op v verandert de snelheid niet).
23)
a) De richting van de stroomsterkte is tegengesteld aan de snelheid van het elektron, dus tegen de klok in. De
lorentzkracht treedt op als middelpuntzoekende kracht en moet dus naar het midden van de cirkel gericht zijn.
Hierdoor volgt met behulp van de linkerhandregel dat de veldlijnen het papier in staan.
b) r = mv / Bq dus v = Bqr / m = 1,5.10-3 . 1,6.10-19 . 0,05 / 9,1.10-31 = 1,3.107 (m/s)
c) bij cirkelbeweging geldt ampz = v² / r = 3,5.1015 (m/s²) naar het midden gericht (grootte snelheid verandert
niet, wel richting!)
d) EK = ½ mv² = 7,91.10-17 (J) = 4,9.102 (eV)
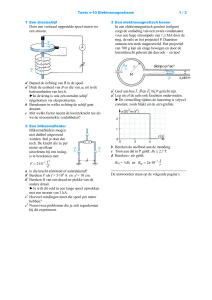
24)
B
25)
Door een metalen plaatje waardoor een stroom loopt in een
magneetveld te brengen buigen de elektronen af. In de tekening
hiernaast buigen ze naar beneden af. Daardoor wordt de onderzijde
van het plaatje negatief geladen en ontstaat er een elektrisch veld
in het plaatje dat de lorentzkracht tegenwerkt. Uiteindelijk geldt
dat de elektrische en magnetische krachten even groot zijn en
daardoor verandert het potentiaalverschil tussen boven- en
onderkant van het plaatje niet meer. Dit is dan te meten met een
voltmeter en is een maat voor de sterkte van het magneetveld
volgens: Bqv = qE
a) De elektrische kracht op de protonen is naar links gericht, de lorentzkracht moet dan naar rechts gericht zijn
om de protonen langs een rechte lijn te laten bewegen. De stroom is naar beneden gericht, dus met de
linkerhandregel volgt dan dat de magnetische veldlijnen het papier in moeten zijn gericht.
b) Bqv = qE ofwel v = E / B = 8,0 .104 / 25.10-3 = 3,2.106 (m/s)
c) Door de grotere snelheid verandert de lorentzkracht die wordt groter dan de elektrische kracht dus de
protonen buigen naar rechts af.
d) Zowel de elektrische kracht als de lorentkracht draait van richting om en verder geldt nog steeds Bqv = qE
dus de elektronen buigen niet af.