Wiskunde Praktische opdracht

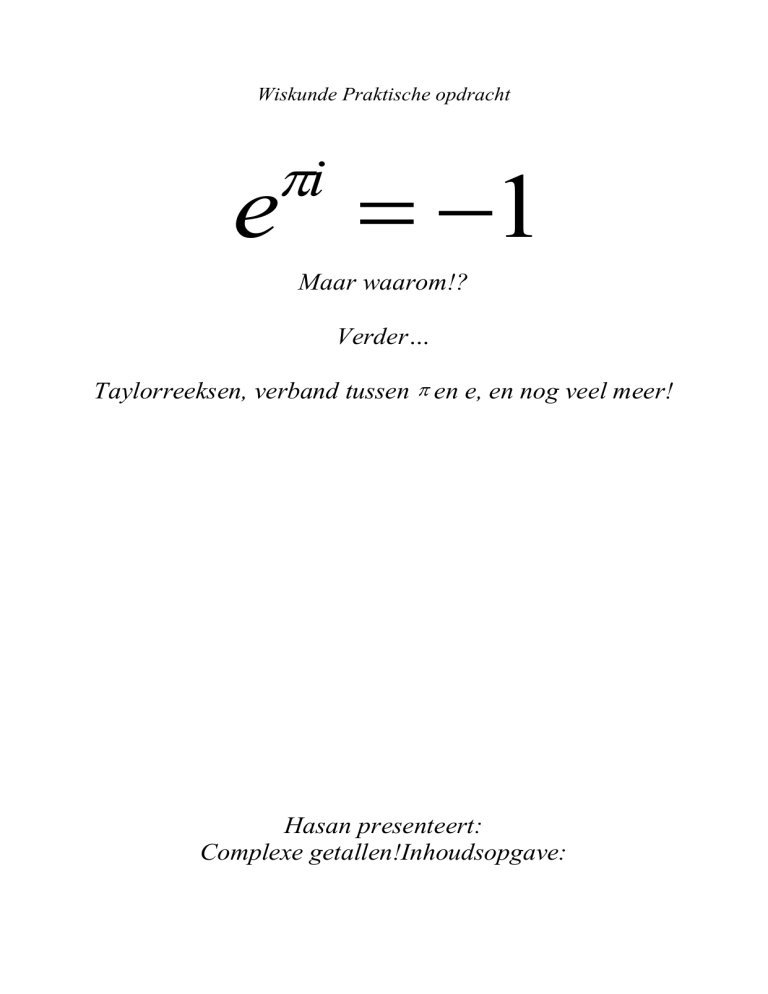
Wiskunde Praktische opdracht
i
e  1
Maar waarom!?
Verder…
Taylorreeksen, verband tussen  en e, en nog veel meer!
Hasan presenteert:
Complexe getallen!Inhoudsopgave:
Complexe getallen: Inleiding
3
Elementaire bewerkingen
3
Vectoren en De Moivre
4
Euler’s formule
5
Vergelijkingen oplossen in het complex vlak
6
Taylorreeksen
8
Definitie van complexe getallen
9
Conclusie
zijn complexe getallen?
10Wat
Altijd al irritant gevonden dat er geen wortels van negatieve getallen bestaan? Er is namelijk
geen enkel cijfer, waarvan het kwadraat -1 geeft. 1x1=1 en -1x-1=1. Wiskundigen vonden niet
prettig, en ze dachten van:
“Weetje wat? Ik bedenk gewoon een getal i , die de wortel is van -1! Zodat
handig!’’, zeiden de slimme wiskundigen! Nu kunnen we vergelijkingen als
i2  1!’’ Wat
x2  1eindelijk oplossen! De “i” staat voor imaginair, want natuurlijk bestaat zo een
getalletje niet. Alle getallen waarin i erin voorkomt, zijn complexe getallen,
bijvoorbeeld 3i  6 .
Van alle andere getalletjes kunnen we een voorstelling maken, maar wat moeten we ons
voorstellen bij de wortel van een negatief getal!? De antwoord hierop is simpel: Net zo goed
dat ½ geen betekenis heeft voor iemand die stenen telt, of dat -3 geen betekenis heeft voor een
voetbal uitslag, heeft i normaal gesproken geen betekenis. Enkel, als je 3 taarten met twee
man wilt delen, komen breuken kijken, of bij je bankrekening hebben negatieve getallen wél
betekenis.
Complexe getallen hebben dus wél betekenis, alleen in vrij ingewikkelde zaken als
quantummechanica en relativiteit. ( Wat ik verder niet zal bespreken).
In het eerste gedeelte van mijn praktische opdracht ga ik focussen op het werken met
complexe getallen, vervolgens ga ik door middel van Taylorreeksen uit uitleggen wat het
verband is tussen  en e. Deze twee constanten hebben namelijk veel met complexe getallen
te maken.
2
Elementaire bewerkingen
Complexe getallen zijn getallen in de vorm van z=a+bi. Als a gelijk is aan 0, is het een zuiver
imaginair getal, als b gelijk is aan 0, is het een zuiver reëel getal. Een zuiver reëel getal (
getallen zoals 6, ½, -9.3 etc) is dus een complex getal waarvan b gelijk is aan 0.
Optellen , aftrekken, vermenigvuldigen en delen met complexe getallen gaat net alsof je de i
5
i

9
)

(
2
i

6
)

(5i

2i)

(9

6)

7i

3
vervangt met bijvoorbeeld x. (
.
Vermenigvuldigen gaat op zelfde
2
i

6
)(
4
i

8
)

2
i
4
i

16
i

24
i

48

8
i

40
i

48
manier: (
.
2
Maar, i 2  1 , dus de antwoord hierop is 40i  40.
Delen gaat enigszins anders:
2
12
i

8
12
i

8
3

3
i

36
i

24
i

36
i

24
36

12
i

24
60

12
i
10
2






i
2
3
i

3
3
i

3
3

3
i

9
i

9
i

9
i

9
18
18
3
3
Zoals je ziet, hebben we van de noemer de geconjugeerde genomen, en daarmee
vermenigvuldigd. Dit is exact hetzelfde term, alleen een negatieve imaginaire gedeelte.
Waarom we dit hebben gedaan, zal later wel duidelijk worden, alhoewel nu het ook wel vrij
vanzelfsprekend is: als je de oorspronkelijke complexe getal vermenigvuldigt met zijn
geconjugeerde, krijg je een term die helemaal reëel is ( in dit geval 18) : met andere woorden,
dan hou je geen i’s over.
Elementaire bewerkingen in het complex vlak, gaan net alsof je de ‘i’ vervangt door
bijvoorbeeld ‘x’.
Vectoren
Alle complexe getallen samen, noemt men het complex vlak.
Nu komt er wat bij kijken wat we al op school hebben gehad: vectoren. Het is namelijk zo dat
je een complex getal kan weergeven in een diagram als een vector.
De imaginaire gedeelte staat op de y-as, en het reële
gedeelte wordt door de x-as vertegenwoordigd. Het
complex getal 4+2i kan je dus vertegenwoordigen door 4
hokjes naar rechts te gaan en twee hokjes omhoog.
Eigenlijk kan je ook getallen als ‘’3’’ in het complex getal
weergeven: Namelijk 3 hokjes naar rechts, en nul omhoog:
Een horizontale lijn dus. Complexe getallen optellen snap je
nu wel beter: Hoe tel je vectoren bij mekaar op?:
Je telt de x-gedeelte’s en de y-gedeelte’s bij elkaar op.
Aangezien we complexe getallen als vectoren kunnen weergeven kunnen we alles wat we met
vectoren deden ook toepassen op complexe getallen.
De complexe getal in de voorbeeld hierboven “4+2i” is zoals je ook kan zien een vector. Als
hieraan “3+i” toevoegt, tel je in feite gewoon twee vectoren bij elkaar op. De antwoord erop is
dan ook “5+3i”.
Vectoren kunnen we ook aangeven met de hoek die het maakt ten opzichte van de x-as, en de
absolute lengte van de ‘’pijl’’. De absolute lengte van de vector hierboven (4+2i), is
2
2
. Dit noemen we de ‘r’( of soms ook de modulus); de r staat voor radius (
4

2
 20
straal.) Vervolgens berekenen we de hoek die het maakt, tegen de klok in. Dat is
2
arctan(
)0
.46
radialen. De hoek die het maakt noemen we de argument. (De “arctan” is de
4
3
inverse tanges.) Maar het zou het zo goed 0,46+2pi kunnen zijn, of 0,46-4pi. Dit is omdat als
je een vector met 2pi ( of een veelvoud ervan) ‘’draait’’, je weer op het oorspronkelijke plek

12

2
i
(20
,tan
())
terugkomt. Dus: 4
.
4
Nu weten we van onze vectoren kennis dat als je r en en de hoek die de vector maakt (  )
weet, je ook de cartesische coördinaten ( dwz. In de vorm van a+bi) kan berekenen. We weten
dat het reële gedeelte ( het gedeelte wat op de x-as ligt) te berekenen is met r*cos(  ) en dat
de imaginaire gedeelte ( de y-as) te berekenen is met r*sin(  ). Samengevat:

b
22
a

bi

(
a

b
,
arctan(
))

(
r
,
)

r
(cos

i
sin
)
.
a
Laten we nu eens gaan kijken naar het vermenigvuldigen van complexe getallen, nu we weten
hoe we complexe getallen als vectoren kunnen weergeven. Stel, we nemen de getallen 3 en
12. Dit zijn zuiver reeele getallen, maar voor even beschouwen we het als complexe getallen,
en dus ook als vectoren. De hoek die ze maken met de x-as is nul.( Want ze zijn zuiver reeel,
zie ook het diagrammetje hierboven.) De absolute lengte van de vector is 3, respectievelijk 12.
Nu gaan we deze twee ‘’complexe ‘’ getallen vermenigvuldigen. Dat is natuurlijk 3*12=36.
Maar stel dat deze twee ‘’complexe’’ , de absolute lengte even lang zou blijven, maar dat het
een hoek maakte met de x-as (zodat het een echte complex getal werd), hoe zou het
vermenigvuldigen dan gaan? Zoals je al wellicht kan voorspellen, vermenigvuldig je de
absolute lengtes ( de modulussen) van de complexe getallen, en tel je de hoeken (
argumenten) die de complexe getallen maken bij elkaar op.
Dat je de hoeken bij elkaar optelt en niet vermenigvuldigd als je twee complexe getallen
vermenigvuldigd, kan je als volgt aantonen: Stel dat je een willekeurig complex getal
vermenigvuldigt met het getal 1. De uitkomt is natuurlijk gelijk aan de complexe getal. De
hoek die het getal 1 maakt met de x-as is nul. Dus je telt de hoeken bij elkaar op,- als je het
zou vermenigvuldigen zou die hoek anders 0 worden. Merk op dat de hoek die het maakt ook
 kan zijn: Dan is het een negatief reëel getal.
In formulevorm:( waarbij z staat voor de absolute lengte, en arg(z) voor de hoek die het
z
z
)

arg
z

arg
z
.
maakt): z1z2 z1  z2 en arg(
1
2
1
2
Stelling van de Moivre: Voor elke waarde van  en elk geheel getal n>0, geldt:
  
n
(cos

i
sin
)

cos(
n
)

i
sin(
n
)
. In feite is de stelling van de Moivre een uitbreiding
van de eerste stelling.
Euler’s theorie
In de vorige paragraaf hadden we laten zien dat je een complexe getal ook kon noteren , door
het voor te stellen als een vector. Hierbij gebruiken we de hoek die de vector maakt en de
lengte van de vector .
Als we de stel complexe getallen nemen , ( z=a+bi), waarvan de modulus ( absolute lengte)
‘’ z ’’, gelijk is aan 1, kunnen we het omschrijven tot:
z

a

bi

(
r
,
)

(
1
,
)

1
(cos

i
sin
)

cos

i
sin
.
Vervolgens vatten we het op als een functie, waarbij we i zien als een constante, en
differentiëren we het:


4


z

cos

i
sin

z
'


sin

i
cos
. Kijk eens! De
afgeleide ervan is haast gelijk aan de oorspronkelijke functie!
De coëfficiënt van cos was 1, dat is i geworden. En de
coëfficiënt van sin was i, dat is -1 geworden! Oftewel: Het is
met i vermenigvuldigd, want i*i=-1! z '  i  z !
Het is vrijwel gelijk aan de oorspronkelijke functie, maar het moet enkel met i worden
vermenigvuldigd. Welke functie is gelijk aan zijn afgeleide? Juist:
zxyi
e x . Aangezien het met i moet worden vermenigvuldigd kunnen we
cos


isin


e. We kunnen dit stellen , omdat
zr(cos
isin
) stellen dat: z
(
0
)
i
i
1

cos(
0
)

isin(
0
)
e
zre
i
Dit geldt voor de complexe getallen waarbij de absolute lengte ( r)
gelijk is aan 1.
Nu hebben we gezien dat er drie manieren zijn om een complex getal op te schrijven: Zie de
‘’tabelletje’’ hiernaast:
Waarin x het reeele deel, y de imaginaire deel, r de absolute lengte van de vector, en  de
hoek die de vector maakt met de x-as, tegen de klok in.
Net zoals optellen en aftrekken erg simpel gaat met de z=a+bi notatie, is vermenigvuldigen en
i
delen met de z  re notatie ( de zogenaamde notatie van Euler) veel simpeler. We hadden
gezegd in de vorige paragraaf dat als je twee complexe getallen vermenigvuldgd, je de
absolute lengtes met elkaar vermenigvuldigd en de hoeken bij elkaar optelt. Bij de notatie van
Euler komen deze twee grootheden voor ( de hoek en de absolute lengte).
1
i
3

i
i
Om het wat duidelijker te maken doen we een voorbeeldje: 3
e2 2
e
6
e2 .
Laten we ook kijken naar de geconjugeerde complex getal, die we ook in de een ander
paragraaf tegenkwamen. Bij een geconjugeerde is de reele gedeelte gelijk, maar is de
imaginaire gedeelte negatief.. ( Zie figuur hiernaast)
De geconjugeerde van een complex getal z, noteert men als z .
Uiteraard kan je weer de polaire vorm gebruiken.. De absolute lengte van z en z is hetzelfde.
( z )Als we de hoek die z maakt  noemen, dan is de hoek van z , -  . Als je z en z
vermenigvuldigd, tel je de hoeken bijelkaar op, zodat je op 0 uitkomt. De absolute lengte
2
vermenigvuldig je metelkaar. Dit is het bewijs dat z z = z .
Echter, ook als je z en z optelt gebeurt er iets bijzonders: Netals bij het vemenigvuldigen
i
geeft het een reeel getal: laten we eens nader bekijken. z Noemen we e , en z is dan
( We stellen de absolute lengte op 1.)Maar we kunnen het ook als
(cos
isin
)en (cos

isin


)opschrijven. Verder weten we dat
e i .
cos(

) cos
en sin(

)sin
. ( Dit kan je makkelijk aan de hand van de grafieken
illustreren).
isin
)+ (cos
isin
)+ (cos

isin


)= (cos
isin
).
Dus, z + z = (cos

i

i

e

e
z

z
Dat kan je vereenvoudigen tot 2 cos  . Oftewel:
.

cos


2
2
5
Hetzelfde kan je ook voor de sinus doen.. Dat is mooi hé! Reken het maar na met je
rekenmachine, dat is exact hetzelfde als de cosinus! ( Wacht maar af, in de laatste paragraaf
gaan we nóg een manier bespreken om weer hetzelfde cosinus weer te geven..)
Vergelijkingen oplossen in het complex vlak
Hetgene wat we de vorige paragrafen hebben gedaan was niet onze voornaamste doel. Onze
voornaamste doel is om vergelijkingen op te lossen in het complex vlak, waarbij we zowel de
oplossen vinden die in het reeele vlak zijn, als in het complex vlak.
De allereenvoudigste vergelijking waarvoor in het reele vlak geen oplossing voor is, is
z2 1  0.
In het complex vlak is het echter heel simpel om zoiets op te lossen:
2
2
z

1

0

z


1

z


i
.
Wiskundigen hebben bewezen ( maar dat doe ik hier niet na!) dat elke vergelijking in de vorm
n
n

1
z

a
z

...

a
z

a

0
n
n

1
1
0
van a
precies n oplossingen heeft. Dit is de hoofdstelling van
2
de algebra. Dit is in overeenstemming met z 1  0, die inderdaad, zoals het hoort, precies
2 oplossing heeft.
Voorbeelden:

i3
33

i

i
z 3  1 . We kunnen dit in de polaire vorm noteren als: (
re
)
r
e


1

1
e
.
Dit betekent dat r3=1 en dus dat r=1, en dat 3φ=π +k*2π. Waarbij k een geheel getal is. Je
doet er nog k*2π bij, omdat als je 2π ‘’verderdraait’’, je weer op hetzelfde uitkomt.
3φ=π +k*2π.  dus φ=(1/3)π +k(2/3)π.
φ is dus: 1/3π , 3/3π of 5/3π. 7/3π kan niet , aangezien dat gelijk is aan 1/3π.
1
1

i
z
1
e

1
(cos
isin
)11i 3
1
3
3
2 2
3
3

i
z2 
1
e

1
(cos
isin
)
1
.
3
3
5
5

i
z
1
e

1
(cos
isin
)11i 3
3
3
3
2 2
6
(z1i) 
i. Ook deze kan men netals de vorige oplossen. Hiervoor stelt
i
3
men: z1i re en i 1e2 .
r6=1 , dus r=1 ( Bij de absolute lengte zijn vanzelfsprekend negatief of complexe getallen niet
mogelijk.)
3
1
1
 k2, dus  k . Volgens de hoofdstelling van de algebra
En verder: 6
2
4
3
zijn er 6 waardes van φ mogelijk, dat kan men zelf nagaan.
i
z2 2z50. Deze vergelijking kunnen we uiteraard met behulp van de abc- formule
oplossen.
Als je het wilt oplossen, door gebruik te maken van deze
formule, kom je erachter dat er geen oplossingen voor zijn,
aangezien dan de discriminant <0 is. Maar in het complex
vlak zijn wél de wortels van negatieve getallen wel toegestaan.
6
2

2

2

4

1

5

2

4
i
.
x

 

1

2
i
1
,
2
2

1
2
Hoe zit het nou met x2=0?
Die heeft toch maar 1 oplossing, namelijk x=0, terwijl de hoofdstelling van de algebra zegt
dat er twee moeten zijn! Nou.. Er zijn eigenlijk wél twee oplossingen van x2=0 , en het is niet
moeilijk dat te snappen..
x2=4 Heeft twee oplossingen, 2 en -2. x2=9 heeft ook twee oplossingen, 3 en -3. Dus het is
aannemelijk dat de x waardes van x2=0 , 0 en -0 is. Maar wat moeten we ons voorstellen bij 0?
i
Laten we deze vergelijking oplossen , door het eerst als re te schrijven.
x2=r2eφi2 ,en 0 is 0+k2π.
Dit betekent dat r2=0, dus r=0. Maar, 2  k2 , dus φ is 0 of π.! Natuurlijk zijn bij beide φ
waardes , de x waarde 0, aangezien de lengte van de vector 0 is..
Maar omdát de lengte van de 0 is, kan het iedere hoek aannemen die het maar wilt,- het blijft
0. !
Bij φ=0, is de ‘’vector’’ met lengte 0 gericht naar rechts, en bij φ= π is het gericht naar links,
naar de kant van de negatieve , reeele getallen. Dat is dus het concept van 0 en -0.
Taylorreeksen
Typ eens in je rekenmachine sum(seq(1/(X!),X,0,20)).. Toevallig..?
sin
i 

e nader bekijken en ook
In deze paragraaf gaan we de vergelijking cos
‘’echt’’ bewijzen. Dit doen we met behulp van Taylorreeksen. Het gaat erom dat je vele
functies kan schrijven als een oneindige polynoom (machtsfuncties) .Dus, voor de functie f(x)
is de Taylororreeks:
f(x) = a0 + a1x + a2x2 + a3x3 + a4x4 +… etc
Voor de meeste functies is het opstellen van zo een taylorreeks niet simpel, maar voor de
functies die voor ons interessant zijn, is het opstellen van een taylorreeks vrij simpel. ( De
functies ex, sin(x) en cos(x) )
We beginnen met f(x)=ex . Dé eigenschap van f(x)=ex is natuurlijk dat de afgeleide functie
gelijk is aan de oorspronkelijke functie: , f'(x)=ex.
i
De taylorreeks van , f(x)=ex is: a0 + a1x + a2x2 + a3x3 + a4x4 +… etc
Als we x=0 invullen komt er uit:
e0 =1= a0 + a1(0) + a2(0)2 + a3(0)3 + a4(0)4 +… etc Dus a0 =1.
De taylorreeks van f’(x)=ex is dus : a1 + 2a2x + 3a3x2 + 4a4x3 +… etc
( Gewoon het afleiden van een machtsfunctie, de a0 verdwijnt, want dat is een constante.)
Weer vullen we x=0 in ( dat doen we altijd bij het berekenen van een taylorreeks)
f’(0)=e0 =1 = a1 + 2a2(0) + 3a3(0)2 + 4a4(0)3 +… etc Dus a1 =1.
De taylorreeks van f’’(x)= 2a2 + 6a3x + 12a4x2 +… etc
7
Als x=0, dan is 2a2=1 Dus a2=1/2
We doen het nog een laatste keer:
De taylorreeks van f’’’(x)= ex=6a3 + 24a4x +… etc
Als x=0, dan is 6a3 =1 Dus a3=1/6
Hopelijk is het nu wel duidelijk dat a4=1/24(=1/4!) en dat a5=1/120(=1/5!).. Zie je de patroon?
Algemeen kunnen we stellen dat: an=1/n! en dat f(x)=ex = 1 + x + (1/2!)x2 + (1/3!)x3 +
(1/4!)x4 + ... + (1/n!)xn.
Nu gaan we hetzelfde doen met f(x)=sin(x). Als je de vorige voorbeeld goed kon volgen, is dit
een eitje:
f(x) = sin(x) = a0 + a1x + a2x2 + a3x3 + a4x4 + ...
f(0) = sin(0) = 0 = a0 + a10 + a202 + a303 + a404 + ... = a0 Dus a0 = 0
f'(x) = cos(x) = a1 + 2*a2x + 3*a3x2 + 4*a4x3 + ...
f'(0) = cos(0) = 1 = a1 + 2*a20 + 3*a303 + 4*a403 + ... = a1 Dus a1 = 1
f"(x) = -sin(x) = 2*a2 + 2*3*a3x + 3*4*a4x2 + ...
f"(0) = -sin(0) = 1 = 2*a2 + 2*3*a3*0 + 3*4*a4*02 + ... = 2*a2 Dus a2 = 0
f"'(x) = -cos(x) = 2*3*a3 + 2*3*4*a4x + ...
f"'(0) = -cos(0) = -1 = 2*3*a3 + 2*3*4*a40 + ... = (2*3)a3 Dus a3 = -1/(2*3)
f""(x) = sin(x) = 2*3*4*a4 + ...
f""(0) = sin(0) = 0 = 2*3*4*a4 + ... = 2*3*4*a4 Dus a4 = 0
Je ziet dat bij a0 , a2 etc ( bij even getallen) , het telkens 0 is
Bij a1 is het 1 ( Oftewel 1!) , bij a3 is het -1(2*3)=-1/(3!).
Algemeen kunnen we stellen dat:
an = 0 als n = even, en an = (-1)(n-1)/2/n! als n = oneven. Het is (-1)(n-1)/2, want eerst haal je van
het oneven getal 1 af, zodat het een even getal wordt. Maar (-1)(n-1) is altijd een postitief getal,
aangezien (n-1) bij n =oneven altijd een even getal geeft. Daarom deel je het door twee, zodat
a3, a7, a11 etc een negatief getal worden.
sin(x) = x - (1/3!)x3 + (1/5!)x5 - (1/7!)x7 + ...
Hetzelfde kunnen we voor de f(x)=cos(x) doen, maar dat laat ik als een oefening aan u over..
Tot nu toe zijn dus bekend:
cos(x) = 1 + (1/2!)x2 + (1/4!)x4 + (1/6!)x6 + ...
sin(x) = x - (1/3!)x3 + (1/5!)x5 - (1/7!)x7 + ...
ex = 1 + x + (1/2!)x2 + (1/3!)x3 + (1/4!)x4 +
Zoals men kan zien, lijken deze vergelijkingen behoorlijk veel op elkaar. Nu gaan we in plaats
van (x) , (ix) invullen.
exi = 1 + (ix) + (1/2!)(ix)2 + (1/3!)(ix)3 + (1/4!)(ix)4 + ..
Aangezien we weten hoe we in moeten schrijven, kunnen we het vereenvoudigen:
eix = 1 + ix - (1/2!)x2 - i(1/3!)x3 + (1/4!)x4 + ...
Nu gaan we cos(x)+i*sin(x) schrijven:
cos(x) + i * sin(x) = 1 + ix - (1/2!)x2 - i(1/3!)x3 + (1/4!)x4 + ... = eix
Nu hebben we de Euler’s formule bewezen, namelijk dat cos(x)+i*sin(x)= eix.
Definitie van complexe getallen
8
Deze paragraaf heb ik bewust aan het eind van mijn PO gezet, aangezien je hopelijk nu
genoeg inzicht en vaardigheden hebt in het werken met complexe getallen. Er is een laatste
fundamentele aspect dat besproken dient te worden; namelijk hoe zijn complexe getallen
gedefinieerd? Met andere woorden: hoe is i gedefinieerd? Het is heel logisch door te denken
dat
i
gedefinieerd is als “ i
  1 ” , maar aangezien wortel(-1) niet bestaat kan dit niet.
De eenheid van het complex vlak, namelijk i , is gedefinieerd in een assenstelsel, met zowel
aan de x als de y-as reele getallen. i is gedefinieerd als de vector, van de oorsprong tot de
coordinaten (0,1). Een streepje met lengte 1, die een hoek maakt van 90 graden dus. Als je
naar de assenstelsel kijkt, dan zie je dat de vector van (0,0) tot (0,1) overeenkomt met i .
Hieruit volgt dat i  1, en hieruit volgt weer dat i   1 .
Dit is enigszins muggenzifterij, maar wiskundig gezien is het niet helemaal juist om te zeggen
2
dat het gedefinieerd is als
i  1 .
Conclusie
Wat is nou het verband tussen  en e? Dat is niet zo één twee drie te zeggen, ik heb voor
mezelf ( en voor u ) getracht het enigszins uit te leggen, hoewel het erg abstract blijft, en ik
i
niet echt weet wat ik moet visualiseren bij e  1. De beste manier om het te
visualiseren blijft toch door deze vergelijking voor te stellen als een vector , opgeschreven in
poolcoördinaten.
Complexe getallen worden veel gebruikt in de wiskunde, vooral om vergelijkingen op te
lossen, maar ook in meer ‘’exotische’’ onderwerpen als de quantummechanica worden ze
gebruikt. Eens had ik bijvoorbeeld gelezen over een hypothetisch deelltje in de natuurkunde ,
waarvan men had berekend dat het een massa had van i .
Ik vond het erg leuk ( Tsja, ik vind wiskunde eenmaal leuk ) om met complexe getallen
kennis te maken, en heb dan ook veel plezier eraan gewerkt.
Logboek:
Eerlijk gezegd heb ik niett bijgehouden wanneer en hoe lang ik heb gewerkt, hopelijk heeft dit
geen invloed op mijn cijfer. Maar ik kan wel noteren waneer ik ongeveer eraan heb gewerkt,
van wat ik nog herinner. Ik heb het niet bijgehouden, omdat ik toch alleen was. Masar vooral
omdat wiskunde eenmaal zo een leuk vak is!
Datum?
Hoe lang?
Wat?
Voorjaarsvakantie
Elke dag een
uurtje ( in totaal
zo ene 7 uur)
Complexe
getallen leren,
voor mij zelf
Eerste twee weken In totaal zo een
maart
10 uur op school
Nog niet begonnen aan
schrijven van PO
Werken in school PO schrijven
aan schrijven van
PO
9
Laatste twee
weken maart
Ook thuis eraan
PO schrijven
werken ( Zo een 4
uur schat ik)
Alles verloopt op
rolletjes! Goed gepland,
ben ruim op tijd klaar!
(Stiekem hoop ik op minstens een 8,5 , maar ik ben ervan overtuigd dat u me dat gunt, ik heb
dan ook echt mijn best gedaan, en ik zou het jammer vinden als u punten zou aftrekken omdat
mijn logboek niet goed is, of ander onbenul.)
Planning? Ik was me al aan het verdiepen in dit onderwerp voordat we de PO opdracht
kregen! Zo leuk en interessant vind ik het dus. In feite heb ik dus geen planning. Uitendelijk
ben ik wel ruim op tijd afgekomen.. ( Nogmaals, hopelijk is dit geen ramp.)
Bronnen:
http://www.math4all.nl/Documenten/Complex.pdf
( Een erg handige ‘’boekje’’ , heb het vooral
hieraan geleerd.)
www.wisfaq.nl ( Voor het stellen van vragen, erg goede website!)
Verder geen bronnen gebruikt.
1
0