Bewijzen hoofdstuk 2

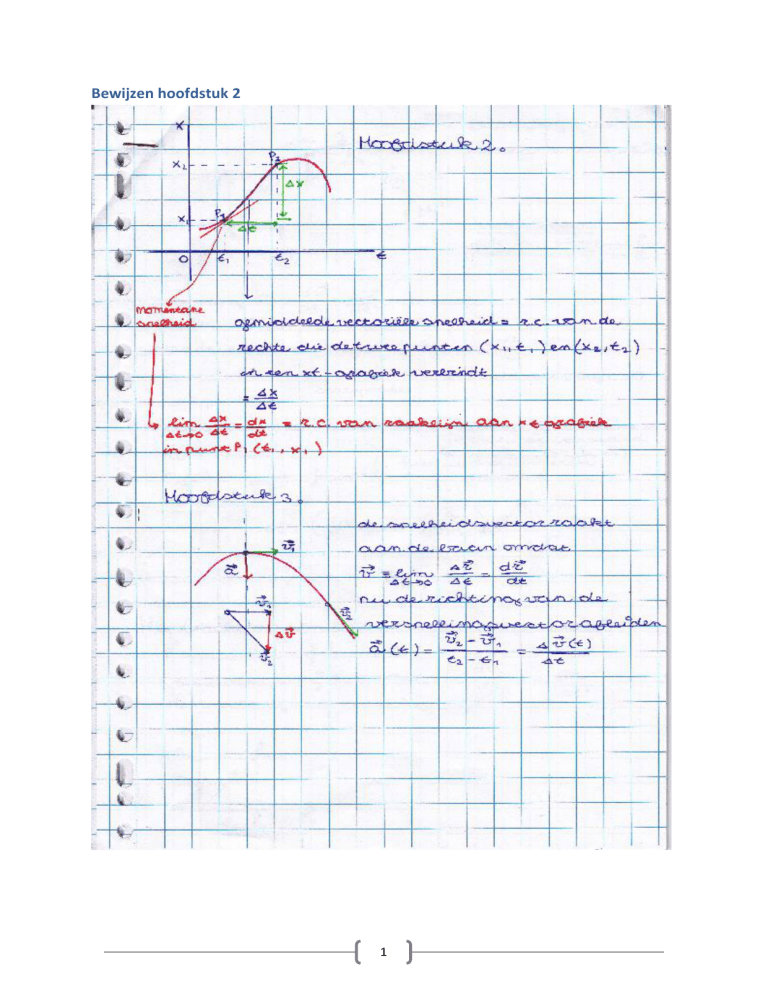
Bewijzen hoofdstuk 2
1
Bewijzen hoofdstuk 3
2
Bewijzen hoofdstuk 5
3
Bewijzen hoofdstuk 6
4
5
Bewijzen hoofdstuk 7&8
6
7
8
9
10
11
Bewijzen hoofdstuk 9
Bewijs H9
∑⃗
⃗
Bewijs H9

⃗⃗⃗⃗⃗⃗⃗⃗
Verband kracht en impuls
⃗
⃗
⃗
Tweede wet van Newton voor een systeem van voorwerpen
∑ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ schrijven in termen van de totale impuls ⃗ van een systeem puntmassa’s
⃗
⃗⃗⃗⃗
⃗⃗⃗⃗
⃗⃗⃗⃗
∑ ⃗⃗⃗
∑ ⃗⃗⃗ volgt dat ⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗⃗
Uit ⃗⃗⃗⃗⃗⃗⃗⃗
de totale impuls van een systeem van puntmassa’s is gelijk aan het product van de totale massa M en
de snelheid van het massamiddelpunt van het systeem
de impuls van een ruimtelijk voorwerp is het product van de massa van het voorwerp en de snelheid
van het MM ervan
⃗
⃗⃗⃗⃗⃗⃗⃗⃗ naar tijd differentiëren levert:
⃗
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗
∑ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ volgt dat
∑ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ → dit is de tweede wet van Newton voor een
Uit ⃗⃗⃗⃗⃗⃗⃗⃗
systeem van voorwerpen (geldig voor willekeurige gesloten systemen van puntmassa’s of
voorwerpen)
Bewijs H9
De tweede wet van Newton voor een systeem
 Een belangrijke reden voor het belang van het concept massamiddelpunt is dat de
translatiebeweging van het MM voor een systeem van puntmassa’s direct gerelateerd is aan de
nettokracht die op het systeem als geheel werkt, bewijs:
⃗⃗⃗⃗⃗⃗⃗
(differentiëren naar de tijd:)
(de afgeleide naar de tijd:)
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
∑
∑
∑
⃗
⃗⃗⃗⃗
of
⃗⃗⃗⃗⃗⃗⃗⃗
∑
⃗⃗⃗
⃗⃗⃗
⃗⃗ dus:) ⃗⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗ ⃗⃗⃗⃗
⃗⃗⃗⃗
∑ ⃗⃗⃗
(de tweede wet van Newton is ⃗⃗⃗
Dat wil zeggen dat de vectorsom van alle krachten die op het systeem werken gelijk is aan de totale
massa van het systeem maal de versnelling van het massamiddelpunt ervan.
De krachten ⃗⃗ die uitgeoefend worden op de puntmassa’s van het systeem kunnen in twee soorten
opgesplitst worden: uitwendige krachten die uitgeoefend worden door voorwerpen buiten het
systeem en inwendige krachten die puntmassa’s binnen het systeem op elkaar uitoefenen. Volgens
de derde wet van Newton treden de inwendige krachten paarsgewijs op: als een puntmassa ene
kracht uitoefent op een tweede puntmassa in het systeem, moet de tweede een even grote en
tegenovergesteld gerichte kracht uitoefenen op de eerste puntmassa. In de som van alle krachten
heffen deze inwendige krachten elkaar dus op.
∑ ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ .
De tweede wet van Newton (voor een systeem) ⃗⃗⃗⃗⃗⃗⃗⃗⃗
Bewijs H9
Elastische botsingen in één dimensie
Behoud van impuls:
→ mA(vA –v’A) = mB(v’B – vB)
Behoud van kinetische energie:
→ mA(v2A –v’2A) = mB(v’2B –
v2B)
dit kunnen we weer omschrijven tot mA(vA –v’A) (vA +v’A) = mB(v’B – vB) (v’B + vB)
We delen de wet van behoud van impuls door de wet van behoud van kinetische energie:
(alleen gebruiken als de botsing eendimensionaal frontaal is!)
12
Bij een willekeurige elastische frontale botsing geldt blijkbaar dat de relatieve snelheid van de twee
voorwerpen na de botsing dezelfde grootte (maar tegengestelde richting) heeft als voor de botsing,
ongeacht hoe groot de massa’s zijn.
Voor een willekeurige elastische frontale botsing geldt dat
(
)
(
) en
(
)
(
)
Bewijs H9
Behoud van impuls
Behoud van impuls afleiden uit de bewegingswetten van Newton:
de kracht die voorwerp A op voorwerp B op een willekeurig moment uitoefent is gelijk aan , volgens
de derde wet van Newton geldt dan dat de kracht die door voorwerp B op voorwerp A uitgeoefend
wordt gelijk is aan en we veronderstellen dat er geen andere uitwendige krachten werken
⃗⃗⃗⃗⃗
&
⃗⃗⃗⃗⃗
→
⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
→ ⃗⃗⃗⃗
Bewijs H9
⃗⃗⃗⃗
Totale impuls/tweede wet van Newton voor een systeem
∑ ⃗⃗⃗
 De totale impuls van een systeem: ⃗
⃗⃗⃗⃗
⃗⃗⃗⃗
⃗⃗⃗⃗
⃗
⃗⃗⃗
∑
∑ ⃗⃗
13
Bewijzen hoofdstuk 10
Bewijs H10
Lineaire snelheid
of
Bewijs H10
Lineaire versnelling
of
De totale lineaire versnelling van een punt op een willekeurig moment is de vectorsom van twee
componenten:
⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗
⃗⃗⃗⃗
Bewijs H10
Traagheidsmoment en krachtmoment
Situatie: een puntmassa met massa m beschrijft een cirkelvormige baan met straal R aan het eind
van een touw of stang, waarvan we de massa kunnen verwaarlozen t.o.v. m, en we veronderstellen
dat er één tangentiale kracht F werkt op m. We gebruiken de tweede wet van Newton voor lineaire
grootheden en de vergelijking voor de hoekversnelling en de tangentiale lineaire versnelling levert:
(beiden zijden vermenigvuldigen met R geeft:)
De grootheid
stelt de rotationele traagheid van de puntmassa voor en wordt het
traagheidsmoment genoemd.
∑
Bewijs H10
Rotationele kinetische energie
Rotationele kinetische energie:
Een willekeurig star roterend voorwerp bestaat uit veel miniscule
puntmassa’s die elk een massa mi hebben. Als we de afstand van een
willekeurig deeltje tot de rotatie-as Ri noemen, is de lineaire snelheid
daarvan vi = Riω. De totale kinetische energie van het hele voorwerp zal
de som zijn van de kinetische energieën van alle deeltjes waaruit het
bestaat:
∑(
)
∑
∑
½ en ω2 worden buiten de sommatie gebracht, omdat zij gelijk zijn voor elk deeltje van een star
voorwerp en ∑(
De kracht
)
[rotatie om een vaste as!]
uitgeoefend op een punt op een afstand R van de rotatie-as verricht arbeid:
∫
waarin
van
∫
een oneindig kleine afstand is, loodrecht op R met grootte dl = Rdɵ, en
loodrecht op R en evenwijdig aan
.
de component is
is het krachtmoment om de rotatie-as, dus:
14
∫
is de verrichte arbeid door een krachtmoment dat een voorwerp wil laten roteren
over de hoek
. De snelheid waarmee de arbeid verricht wordt, het vermogen P,:
Het principe van arbeid en energie is geldig voor de rotatie van een star voorwerp om een vaste as:
(waarin we de kettingregel gebruikten en
In dit geval is
en
∫
)
∫
De verrichte arbeid bij het roteren van een voorwerp is gelijk aan de verandering van de rotationele
kinetische energie van het voorwerp.
Bewijs H10
Rotationele plus translationele beweging
Een voorwerp dat om het massamiddelpunt roteert en een translatiebeweging ondergaat, zal zowel
translationele als rotationele kinetische energie bezitten.
Ktot kunnen we schrijven in termen van het massamiddelpunt m.b.v. de verschuivingsstelling: IP = IMM
+ MR2, waarin we R gesubstitueerd hebben voor h. Dus geldt dat:
Maar Rω = vMM ->
(waarin vMM de lineaire snelheid van het MM is, IMM het traagheidsmoment om een as door het MM,
ω de hoeksnelheid om deze as en M de totale massa van het voorwerp)
Bewijs H18
Verband tussen hoeksnelheid en lineaire snelheid
Bewijs H10
Krachtmoment
15
Bewijs H10
Traagheidsmoment
16
Bewijs H10
Voorwaarde voor zuiver rollen
17
Bewijzen hoofdstuk 11
Bewijs H11
Impulsmoment/tweede wet van Newton voor rotatie
Tweede wet van Newton voor rotatie in termen van impulsmoment: ∑
Bewijs H11
(
)
Impulsmoment van een puntmassa
Situatie: een puntmassa met massa m heeft een impuls en een
positievector t.o.v. de oorsprong O in een bepaald inertiaalstelsel. Het
⃗ ⃗
impulsmoment ⃗ : ⃗
Impulsmoment is een vectoriële grootheid. De richting ervan staat
loodrecht op zowel als volgens de rechterhandregel. De grootte ervan
is:
De relatie tussen impulsmoment en krachtmoment;
⃗
⃗
∑
⃗
⃗
∑
⃗
∑
∑⃗
∑⃗
⃗
⃗
⃗
∑⃗
⃗
∑⃗
De verandering van impulsmoment van een puntmassa in de tijd is gelijk aan het netto
krachtmoment dat erop uitgeoefend wordt.
18
⃗
Bewijs H11
De verandering van het totale impulsmoment van een systeem van
puntmassa’s in de tijd is gelijk aan het netto uitwendige
krachtmoment op het systeem. De tweede wet van Newton.
⃗ 𝑴𝑴
𝒅𝑳
𝒅𝒕
Bewijs H11
∑ 𝝉⃗⃗⃗⃗⃗⃗⃗⃗⃗
𝑴𝑴
𝒛𝒆𝒍𝒇𝒔 𝒃𝒊𝒋 𝒗𝒆𝒓𝒔𝒏𝒆𝒍𝒍𝒊𝒏𝒈 𝒐𝒇 𝒗𝒆𝒓𝒕𝒓𝒂𝒈𝒊𝒏𝒈
⃗ is de positievector van de i-de puntmassa in een inertiaalstelsel en ⃗⃗⃗⃗⃗⃗⃗
de positievector van het massamiddelpunt van het systeem in dit
referentiestelsel
⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗
De positie van de i-de puntmassa t.o.v. het MM is ⃗⃗⃗ : ⃗⃗⃗
vermenigvuldig elke term met mi en bepaal de afgeleide
⃗
⃗⃗⃗⃗
⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗
(⃗⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗ )
∑ ⃗⃗⃗
Het impulsmoment t.ov. van het MM is: ⃗⃗⃗⃗⃗⃗⃗⃗
∑ ⃗⃗⃗
⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗
de tijdsafgeleide daarvan is:
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
∑
⃗⃗⃗⃗
⃗⃗⃗⃗⃗
de eerste term aan de rechterkant is ⃗⃗⃗⃗
(sinɵ=0) →
⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
∑ ⃗⃗⃗
⃗⃗⃗
⃗⃗⃗⃗ en is gelijk aan nul, omdat ⃗⃗⃗⃗ evenwijdig is aan zichzelf
uit de tweede wet van newton volgt dat:
⃗⃗⃗
∑ ⃗⃗⃗
⃗⃗⃗
∑ ⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗
de tweede term aan de rechterkant is nul, ∑
⃗⃗⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗
∑ ⃗⃗⃗
⃗⃗⃗ )
(∑
⃗⃗⃗⃗⃗⃗⃗ en ⃗⃗⃗⃗⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗
per definitie
⃗⃗ waarin ⃗⃗ de nettorkacht op mi is
⃗⃗⃗
∑ ⃗⃗⃗
⃗⃗⃗⃗⃗⃗⃗⃗
19
∑ ⃗⃗⃗⃗⃗⃗⃗⃗
Bewijs H11
Impulsmoment en krachtmoment voor een star voorwerp
Voor elke puntmassa van het voorwerp is: ⃗⃗⃗
⃗ ⃗⃗⃗
De component van ⃗⃗⃗ langs de roatie-as is:
De som over alle puntmassa’s:
(∑
∑
∑
)
De component van het totale impulsmoment langs de rotatie-as is dus:
20
Bewijzen hoofdstuk 18
Bewijs H18
Druk
Hoe groot is de druk die een gas uitoefent op een vat?
Stel de moleculen voor binnen een rechthoek vat waarvan de uiteinden een oppervlakte A hebben
en waarvan de lente l is. De druk die door het gas op de wanden van het vat wordt uitgeoefend is
een gevolg van de botsingen van de moleculen met de wanden. Wanneer een molecuul een kracht
uitoefent op de wand oefent de wand een gelijke en tegengestelde reactiekracht uit op het molecuul
(derde wet van Newton). Op grond van de tweede wet van Newton is de grootte van deze kracht op
het molecuul gelijk aan de impulsverandering van het molecuul, F = dp/dt. Ervan uitgaande dat de
botsing elastisch is, verandert alleen de x-component van de impuls van het molecule, van –mvx tot
+mvx.
Dit molecuul zal vaak botsen met de muur, met tussenpozen van Δt, de tijd die het molecuul nodig
heeft om in het vat een afstand (x-component) heen en terug af te leggen, dat wil zeggen 2l.
De tijd Δt tussen de botsingen is erg kort, dus is het aantal botsingen per seconde erg groot. Dus is de
gemiddelde kracht gelijk aan de impulsverandering gedurende één botsing gedeeld door de tijd
tussen botsingen:
De feitelijke kracht als gevolg van één molecuul fluctueert, maar omdat elke seconde een groot
aantal moleculen de wand raakt, is de kracht gemiddeld genomen vrijwel constant.
De nettokracht op de wand (de kracht als gevolg van alle moleculen in het vat):
. Met de gemiddeld waarde van de x-component van de snelheid is: ̅̅̅
̅̅̅
We kunnen de kracht dus schrijven als
Voor elke vector geld dat het kwadraat van de grootte ervan gelijk is aan de som van de kwadraten
van de componenten: ̅̅̅ ̅̅̅ ̅̅̅ ̅̅̅. Omdat de snelheden van de moleculen in het gas
willekeurig worden verondersteld, is er geen voorkeursrichting. Dus geldt ̅̅̅
̅̅̅̅
Dit substitueren we in de vergelijking voor de nettokracht F:
De druk op de wand is dan:
̅̅̅̅
̅̅̅̅
oftewel
̅̅̅
met V = lA
̅̅̅
̅̅̅ is de gemiddelde kinetische energie ̅ van de moleculen in het gas. Bovenstaande
vergelijking vergelijken met de ideale gaswet
levert ( ̅̅̅)
oftewel
De grootheid
verband tussen temperatuur en gemiddelde kinetische energie van moleculen
̅
̅̅̅
21
Bewijs H18
Diffusie
Diffusie: deeltjes gaan spontaan van regio met hoge concentratie naar regio met lage concentratie
(passief proces).
Een buis met dwarsdoorsnede A met links moleculen in een hogere
concentratie dan rechts. Er zal een nettostroom van moleculen naar
rechts zijn. Een klein deel van de buis met lengte Δx wordt doorkruist
door moleculen uit zowel gebied 1 als gebied 2. Naarmate er zich meer
moleculen in een gebied bevinden, zullen er meer een gegeven
oppervlak raken of een grens passeren. Omdat er in gebied 1 een
hogere concentratie moleculen is dan in gebied 2, zullen er meer
moleculen uit gebied 1 het centrale gedeelte doorkruisen dan uit
gebied 2. Er is dus een nettotransport van moleculen van links naar
rechts, van hoge concentratie naar lage concentratie. De nettostroom
wordt alleen dan gelijk aan nul wanneer de concentraties aan elkaar gelijk geworden zijn.
De diffusiesnelheid J (aantal deeltjes ΔN doorheen doorsnede A in een tijd Δt) is recht evenredig met
het verschil in concentratie per eenheidsafstand oftewel de concentratiegradiënt (C1-C2)/Δx, met de
oppervlakte van de dwarsdoorsnede A en de duur van het tijdsinterval Δt. (Aanname: concentraties
C1 en C2 constant.)
de diffusievergelijking (de wet van Fick):
(met D is de evenredigheidsconstante in m2/s → diffusiecoëfficiënt en Δx in meter)
J is de deeltjesflux en de deeltjesstroom per oppervlak
3
concentraties in mol/m → J is het aantal mol dat per seconde een gegeven punt passeert
concentraties in kg/m3 → J is de massa die per seconde een bepaald punt passeert (kg/s)
22
Bewijzen hoofdstuk 19
Bewijs H19
Inwendige energie
Inwendige energie: de totale energie van alle moleculen binnen het voorwerp.
De inwendige energie van n mol van een ideaal eenatomig gas is de som van de translatie-energieën
van alle atomen → de gemiddelde kinetische energie per molecuul maal het totaal aantal moleculen
̅̅̅
m.b.v. ̅
Bewijs H19
̅̅̅
kunnen we dit schrijven als
oftewel
Isotherm proces (cte T)
De eerste hoofdwet van de thermodynamica:
De temperatuur en de massa worden constant gehouden, de inwendige
energie verandert niet:
. Dus geldt op de grond van
de eerste wet van de thermodynamica,
dus W=Q:
de arbeid die door het gas in een isotherm proces wordt uitgevoerd is
gelijk aan de warmte die wordt toegevoegd aan het gas.
Adiabatisch proces (Q=O / geen warmtestroom)
Bewijs H19
Q=0 dus
Dat wil zeggen: als het gas uitzet, neemt de inwendige energie af; dus
neemt ook de temperatur af.
Bewijs H19
Isobare en isovolumetrische processen
Een isobaar proces is een proces waarbij de druk constant wordt
gehouden. Een isovolumetrisch proces is een proces waarbij het volume
niet verandert (ΔV=0 zorgt dat W=0).
Isobaar proces:
en isovolumetrisch
proces:
23
Bewijs H19
Arbeid en volumeveranderingen
Arbeid die wordt uitgevoerd bij volumeveranderingen
Stel dat we een gas hebben in een cilindrisch vat met een beweegbare zuiger. Kies als
systeem het gas; de wanden en de zuiger maken deel uit van de omgeving. Arbeid
bepalen die door het gas wordt verricht wanneer het quasistatisch uitzet, zodat P en
T op elk moment gedefinieerd zijn voor het systeem.
Het gas zet uit tegen de zuiger met oppervlakte A. Het gas oefent een kracht F=PA uit
op het gas, waarin P de druk in het gas is. De arbeid die door het gas wordt verricht
voor een oneindig kleine verplaatsing van de zuiger is
omdat een oneindig kleine volumetoename gelijk is aan
. Bij een
eindige volumeverandering van VA naar VB zou de door het gas verrichte arbeid W
gelijk zijn aan
∫
∫
.
24
Bewijs H19
Verband tussen CP en CV
Vergelijk isovolumetrisch en isobaar proces waarbij de temperatuur met eenzelfde waarde
toeneemt.
 Isovolumetrisch: er wordt geen arbeid verricht omdat
; dus toegevoegde warmte
wordt volledig omgezet in inwendige energie
 Isobaar: er wordt wel arbeid verricht; dus toegevoegde warmte wordt omgezet in inwendige
energie en arbeid
[constant volume]
[constante druk]
Combineren van de twee vergelijkingen:
Voor een proces bij constante druk geldt
:
of na vereenvoudiging;
.
Omdat de gasconstante R=8,341 J/mol.K is CP circa 8,31J/mol.K groter dan CV.
Bij een ideaal monoatomisch gas is de inwendige energie gelijk aan de totale kinetische energie van
alle moleculen:
(
̅̅̅)
25
Bewijzen hoofdstuk 21
Bewijs H21
Puntlading & Continue ladingsverdeling.
Bewijs H21
Versnelling en afbuiging van elektronenbundels.
26
Bewijzen hoofdstuk 23
Bewijs H23
Elektrische potentiële energie
Situatie: het elektrisch veld tussen twee evenwijdige platen met een even
grote, maar tegengestelde lading; we veronderstellen dat de afstand tussen
de platen klein is in vergelijking met hun breedte en hoogte, zodat het veld ⃗
in het grootste deel van het gebied tussen de platen homogeen zal zijn. Bekijk
een minuscule positieve puntlading q in een punt erg dicht bij de positieve
plaat. Deze lading q is zo klein dat deze geen effect heeft op ⃗ . Als deze lading
q ter plaatse van een punt a wordt losgelaten, zal de elektrische kracht arbeid
op de lading verrichten en deze versnellen in de richting van de negatieve
plaat. De arbeid W die door het elektrisch veld E wordt verricht om de lading
over een afstand d te verplaatsen is
De verandering van de elektrische potentiële energie is gelijk aan het
tegengestelde van de door de elektrische kracht verrichte arbeid:
[homogeen ⃗ ]
Bewijs H23
Relatie tussen elektrisch potentiaal en elektrisch veld
Het verschil in potentiële energie tussen twee willekeurige punten in de ruimte, a en b, wordt
beschreven door:
∫ ⃗
 Het potentiaalverschil is
 Het elektrisch veld ⃗ in een willekeurig punt in de ruimte is de kracht per eenheid van lading:
⃗
Deze twee relaties in bovenstaande vergelijking substitueren levert:
∫ ⃗
Bewijs H23
Elektrische potentiaal als gevolg van puntladingen
De elektrische potentiaal op een afstand r van één enkele puntlading Q kan
∫ ⃗
Het elektrisch veld als gevolg van één enkele puntlading heeft een grootte:
rechtstreeks worden afgeleid uit
of
en is radiaal naar buiten gericht vanuit een positieve lading (of naar binnen gericht als
Q<0).
Bereken de integraal lang een (rechte) veldlijn van punt a, op een afstand ra van Q,
naar punt b, op een afstand rb van Q. In dit geval zal evenwijdig zijn aan ⃗ en
. Dus geldt dat
∫ ⃗
∫
Het is gebruikelijk om de potentiaal nul te kiezen in punten die oneindig ver zijn verwijderd (stel Vb=0
ter plaatse van rb= ). In dat geval is de elektrische potentiaal V op een afstand r van één enkele
puntlading gelijk aan
[één enkele puntlading; V=0 ter plaatse van r= ]
27
Bewijs H23
Potentiaal veroorzaakt door dipool
28
Bewijzen hoofdstuk 24
Bewijs H24
Capaciteit van vlakke condensator
Bewijs H24
Capaciteit van een condensator
De relatie tussen het elektrisch veld en de elektrische potentiaal is
∫ ⃗
We kunnen de lijnintegraal bepalen langs een baan antiparallel met de veldlijnen
(dus in tegenovergestelde richting van de veldlijnen), dus van plaat a naar plaat b,
waarbij geldt dat
en
, dus
∫
∫
∫
Dit levert een relatie tussen Q en V en daarmee kunnen we de capaciteit C
bepalen in termen van de geometrie van de platen:
[condensator met evenwijdige platen]
Bewijs H24
Condensator opladen
De benodigde arbeid om een kleine hoeveelheid lading dq toe te voegen wanneer er een
potentiaalverschil V over de platen aanwezig is, is
. Omdat
op een willekeurig
tijdstip, waarin C de capaciteit is, is de benodigde arbeid om een totale lading Q op te slaan gelijk aan
∫
∫
De energie opgeslagen in een condensator is
wanneer de twee geleiders van de condensator C ladingen +Q en –Q bezitten. Omdat
,
waarin V het potentiaalverschil is over de condensator, kunnen we ook schrijven dat
.
Het is handig om de energie die is opgeslagen in een condensator te beschouwen als energie die is
opgeslagen in het elektrisch veld tussen de platen.
We hebben gezien dat het elektrisch veld ⃗ tussen twee evenwijdige platen die zich dicht bij elkaar in
de buurt bevinden homogeen is en de grootte ervan als volgt aan het potentiaalverschil is
gerelateerd:
, waarin d de afstand tussen de platen is.
voor een condensator met
evenwijdige platen.
(
Dus geldt dat
)(
)
(geldig voor elk willekeurig gebied in de ruimte waar een elektrisch veld aanwezig is)
(
met eenheid (C2/N.m2)(N/C)2=N/m2=(N.m)/m3=J/m3)
(de grootheid Ad is het volume tussen de platen waarin het elektrisch veld E aanwezig is)
29
Bewijs H24
Parallelschakeling van condensatoren
Bewijs H24
Serieschakeling van condensatoren
30
Bewijzen hoofdstuk 25
Bewijs H25
Het vermogen P
De snelheid waarmee energie wordt omgezet in een weerstand R:
( )
Bewijs H25
Wisselstroom
.
Het vermogen is altijd positief. De grootheid
varieert tussen 0 en 1 en het is niet al te moeilijk
om aan te tonen dat de gemiddelde waarde ervan ½ is. Het gemiddelde omgezette vermogen ̅ :
̅
. Het vermogen kan ook worden geschreven als
( )
, dus het
gemiddelde vermogen is gelijk aan ̅
De vierkantswortel van elk van deze termen is de rms-waarde (root-mean-square; kwadratisch
gemiddelde), ookwel de effectieve waarde, van de stroom of de spanning:
√̅
√ ̅̅̅̅
√
√
̅
̅
̅
Een gelijkstroom met waarden I en V gelijk aan de rms-waarden I en V van een wisselstroom zal
hetzelfde vermogen leveren als die wisselstroom.
Bewijs H25
Driftsnelheid en stroom
De driftsnelheid kan gerelateerd worden aan de macroscopische stroom I in de draad.
In een tijd Δt leggen de elektronen gemiddeld een afstand l=vdΔt af. Veronderstel dat
de draad een dwarsdoorsnede met oppervlakte A heeft. In dat geval zullen in een tijd
Δt de elektronen in een volume
de dwarsdoorsnede A van de draad
passeren (zie afbeelding). Als er n vrije elektronen (elk met een lading –e) per eenheid
van volume (n=N/V) zijn, is de totale lading ΔQ die het oppervlak A passeert in een tijd
Δt gelijk aan
De stroom I in de draad is dus
De grootte van de stroomdichtheid,
| |
, is
In vectorvorm is dit
31
⃗⃗⃗⃗
waarin het minusteken aangeeft dat de richting van de (positieve) stroom tegengesteld is gericht aan
de driftsnelheid van de elektronen.
∑
⃗⃗⃗⃗⃗⃗
(verschillende soorten ionen, die elk een dichtheid ni hebben (aantal per eenheid van volume), een
lading qi (qi=-e voor elektronen) en een driftsnelheid ⃗⃗⃗⃗⃗ , is de resulterende stroomdichtheid in een
willekeurig punt gelijk aan bovenstaande vergelijking)
De totale stroom I door een oppervlak A loodrecht op een homogene is dan | |
Bewijs H25
Microscopische vorm van de wet van Ohm
schrijven in termen van microscopische grootheden.
.
en
(bij de laatste vergelijking veronderstellen we dat het elektrisch veld binnen de draad homogeen is en
dat l de lengte is van de draad (of een deel van de draad) waarover tussen de uiteinden een
potentiaalverschil V staat)
(
)
dus
waarin
de geleidbaarheid is
en niet afhankelijk van V (en daarom ook niet van E). De
stroomdichtheid is dus recht evenredig met het elektrisch veld ⃗ in de geleider. Dit is de
⃗
⃗
microscopische variant van de wet van Ohm, in vectorvorm
Bij een metalen geleider zijn
32
Bewijzen hoofdstuk 26
Bewijs H26
Klemspanning
Wanneer er een stroom I op natuurlijke manier uit de batterij stroomt (dus van de pluspool naar de
minpool), is er een inwendige daling van het potentiaalverschil van de batterij die gelijk is aan Ir. De
klemspanning is dan
.
Bewijs H26
Verband tussen klemspanning en bronspanning
Bewijs H26
Weerstanden in serie en parallel
33
Bewijs H26
Condensator opladen
Wanneer de schakelaar S gesloten wordt begint er een stroom door de schakeling te lopen.
Elektronen zullen vanuit de negatieve pool van de batterij door de weerstand R stromen en zich
verzamelen op de bovenste plaat van de condensator. Ook zullen er elektronen naar de positieve
pool van de batterij stromen, waardoor een positieve lading op de andere plaat van de condensator
ontstaat. Naarmate er meer lading op de condensator komt, neemt het potentiaalverschil erover
(
) toe en de stroom neemt af tot het potentiaalverschil over de condensator gelijk
geworden is aan de emk van de batterij, . Er is dan geen potentiaalverschil over de weerstand en er
loopt geen stroom meer. Het potentiaalverschil over de condensator neemt dus in tijd toe
(afbeelding b). De wiskundige vorm van deze kromme, dat wil zeggen als functie van de tijd, kan
afgeleid worden met de wet van behoud van energie (of de tweede wet van Kirchhoff). De emk van
de batterij zal gelijk zijn aan de som van het potentiaalverschil over de weerstand (IR) en dat over de
condensator (Q/C):
de weerstand R is de totale weerstand van de schakeling, inclusief de inwendige weerstand van de
batterij; I de stroom in de schakeling op een willekeurig moment en Q de lading op de condensator op
datzelfde moment
Hoewel , R en C constanten zijn, zijn zowel Q als I veranderlijk in de tijd. De snelheid waarmee
lading door de weerstand stroomt (I=dQ/dt) is gelijk aan de snelheid waarmee lading zich verzamelt
op de condensator. Dus kunnen we schrijven
(
)
Integreren van t=0, als Q=0, tot een tijdstip t wanneer er een lading Q op de condensator aanwezig
is:
∫
∫
|
34
|
(
)
Neem de antilogaritme van beide zijden:
Het potentiaalverschil over de condensator is VC = Q/C, dus
De lading Q op de condensator en het potentiaalverschil VC over de condensator nemen pas na een
erg lange tijd toe van nul op t=0 tot hun maximale waarden Qmax = Q en VC= . De grootheid RC in de
exponent wordt de tijdconstante van de schakeling genoemd:
.
Deze grootheid stelt de tijd voor die de condensator nodig heeft om (1-e-1) = 0,63 of 63% van zijn
maximale lading en zijn maximale potentiaalverschil te bereiken.
De stroom I door de schakeling
Op t=0 is de stroom dus
, zoals te verwachten was voor een schakeling met alleen een
weerstand (er is nog geen potentiaalverschil over de condensator). De stroom neemt dan
exponentieel af in de tijd met een tijdconstante die gelijk is aan RC, terwijl het potentiaalverschil over
de condensator toeneemt. De tijdconstante RC stelt de tijd voor waarin de stroom daalt naar 1/e
0,37 van de initiële waarde.
Bewijs H26
Condensator opladen
Een condensator die al geladen is kan ontladen over een weerstand R.
Het potentiaalverschil over de weerstand op een willekeurig moment is gelijk aan dat over de
condensator:
De snelheid waarmee lading de condensator verlaat is gelijk aan het tegengestelde van de stroom
door de weerstand,
, omdat de condensator bezig is te ontladen (Q neemt af). We
schrijven de vergelijking hierboven nu als
of
.
Vervolgens integreren van t=0 wanneer de lading op de condensator gelijk is aan Q0 tot een bepaald
tijdstip t wanneer de lading op de condensator Q geworden is:
of
Het potentiaalverschil over de condensator (VC=Q/C) als functie van de tijd is
waarin het beginpotentiaalverschil
is. De lading op de condensator en het
potentiaalverschil erover nemen dus exponentieel in de tijd af met een tijdsconstante RC. De stroom
is
en ook deze neemt exponentieel in de tijd af met dezelfde tijdconstante RC. De lading op de
condensator, het potentiaalverschil erover en de stroom in de weerstand nemen allemaal tot 37%
van hun oorspronkelijke waarde af in één tijdsconstante
.
35
Bewijzen hoofdstuk 27
Bewijs H27
Bewijs H27
Magnetische kracht op een bewegende lading in een magneetveld
Vrij bewegende geladen deeltjes ondervinden ook een kracht wanneer ze door een magnetisch veld
passeren. Als N van dergelijke deeltjes met een lading q in een tijd t een bepaald punt passeren,
vormen ze een stroom
. We stellen t gelijk aan de tijd die een lading q nodig heeft om een
afstand in een magnetisch veld ⃗ te overbruggen. In dat geval geldt
, waarin de snelheid
van het deeltje is. De kracht op deze N deeltjes is ⃗
De kracht op één van de N deeltjes: ⃗
⃗
⃗⃗
36
⃗⃗
( ) ⃗
⃗⃗
⃗
⃗⃗
Bewijs H27
Kracht van magnetische inductie op een stroomgeleider
Bewijs H27
De baan van een geladen deeltje dat beweegt in een vlak loodrecht
op een homogeen magnetisch veld is cirkelvormig.
Het elektron beweegt met de klok mee. Een positief deeltje in dit veld zou
een kracht in tegengestelde richting ondervinden en dus tegen de klok in
bewegen.
De richting van het magnetisch veld is in de pagina gericht. Een elektron
in punt P beweegt naar rechts en de kracht op dit elektron in dit punt is
verticaal omlaag gericht. Omdat de kracht altijd loodrecht op staat,
verandert de grootte van niet: het elektron beweegt met een snelheid
met constante grootte. Als de kracht op een deeltje altijd loodrecht op de
snelheid ervan staat, beschrijft het deeltje en cirkelvormige baan en
heeft een centripetale versnelling
.
Een geladen deeltje beschrijft dus een cirkelvormige baan met een
constante centripetale versnelling in een homogeen magnetisch veld.
Substitueren van F en a in de tweede wet van Newton levert:
∑
→
De tijd T die een deeltje met een lading q en een constante snelheid v nodig heeft om een
cirkelvormige omwenteling in een homogeen magnetisch veld ⃗ te beschrijven (
) is
waarin
de omtrek van de cirkelvormige baan is.
37
,
Bewijs H27
Krachtmoment op een stroomlus; magnetisch dipoolmoment
Een elektrische stroom in een gesloten draadlus, die in een uitwendig magnetisch veld is geplaatst →
magnetische kracht op de stroom kan een krachtmoment veroorzaken.
Er loopt een stroom door de rechthoekige lus, waarvan het vlak evenwijdig is aan ⃗ .
⃗ oefent geen kracht en geen krachtmoment uit op de horizontale segmenten van de draad, omdat
deze evenwijdig zijn aan het veld en sin nul is. Het magnetisch veld oefent wel eenkracht uit op elk
van de verticale segmenten van de draad: ⃗ 1 en ⃗ 2. De richting van de kracht op de stroom verticaal
omhoog links is tegengesteld aan de richting van de even grote kracht ⃗ 2 op de stroom vertikaal
omlaag rechts. Deze krachten veroorzaken een resulterend krachtmoment dat de winding om de
verticale as wil laten draaien.
De grootte van het krachtmoment
met a de lengte van de verticale arm van de lus → de arm voor elke kracht is b/2, waarin b
de breedte van de lus is waarvan de ‘as’ zich in het middelpunt bevindt
De krachtmomenten die geproduceerd worden door ⃗ 2 en ⃗ 2 werken in dezelfde richting, dus het
totale krachtmoment is de som van de twee krachtmomenten:
waarin A = ab de oppervlakte van de lus is
Als de lus bestaat uit n windingen, zal de stroom NI zijn, en het krachtmoment
Als de lus een hoek
maakt met het magnetisch veld veranderen de krachten niet, maar hun arm is
wel afgenomen van ½ b tot ½ b sin . De hoek is de hoek tussen ⃗ en de loodlijn op het vlak van de
lus. Het krachtmoment wordt dus
niet alleen geldig voor een rechthoekige spoel, maar voor elke willekeurige andere vorm van een
vlakke spoel
NIA = het magnetisch dipoolmoment van de spoel, beschouwd als een vector:
waarin de richting van
(en dus van ) loodrecht op het vlak van de spoel staat en gegeven wordt
door de rechterhandregel
Dus
⃗ ⃗⃗
⃗
of (geeft de correcte grootte en richting voor het krachtmoment aan)
⃗
⃗ ⃗⃗
Om een stroomvoerende draadlus te roteren waarbij groter wordt, moet arbeid verricht worden
tegen het krachtmoment als gevolg van het magnetisch veld. De potentiële energie hangt dus als
volgt af van de hoek (zie het principe van arbeid en energie voor rotationele beweging):
38
∫
Als we U=0 kiezen voor
∫
is de arbitraire constante C nul en is de potentiële energie
⃗
39