Document

Herhaling hoofdstuk 3: Krachten
•
•
•
•
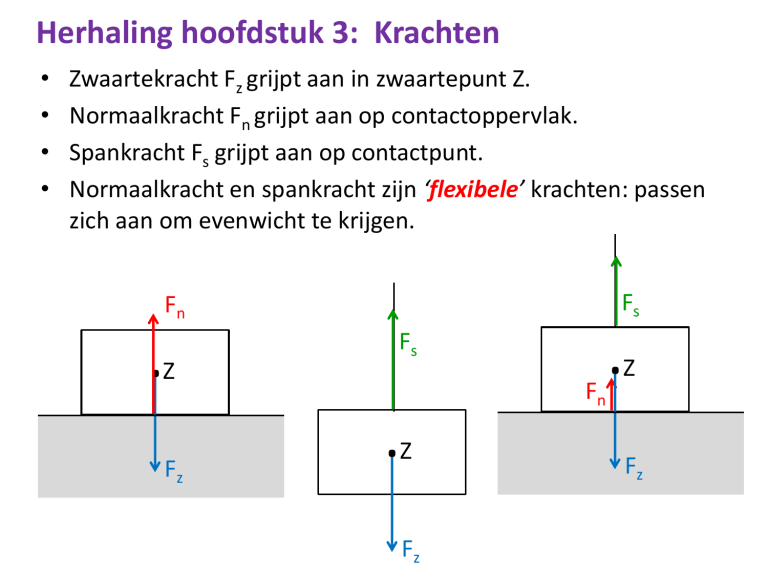
Zwaartekracht Fz grijpt aan in zwaartepunt Z.
Normaalkracht Fn grijpt aan op contactoppervlak.
Spankracht Fs grijpt aan op contactpunt.
Normaalkracht en spankracht zijn ‘flexibele’ krachten: passen
zich aan om evenwicht te krijgen.
Fs
Fn
.
Z
Fz
Fs
Fn
.
Z
Fz
.Z
Fz
§3.4: Krachten in evenwicht
Evenwicht:
𝐹=0
Voorbeeld: construeer de ontbrekende krachten zodat er evenwicht is
F3
F1
F2
F2
F1
F3?
Krachten optellen d.m.v. rekenen
Krachten optellen:
𝐹 betekent
F12,y
𝐹𝑥 en
𝐹𝑦
F12
𝐹12, 𝑦 = 𝐹1, 𝑦 + 𝐹2, 𝑦
𝐹12, 𝑥 = 𝐹1, 𝑥 + 𝐹2, 𝑥
F2,y
(let op mintekens)
F1
F1,y
F2
F12,x
F1,x
F2,x
𝐹12 =
𝐹12, 𝑥2 + 𝐹12, 𝑦2
Krachten op helling
Een blok wordt op een gladde helling (𝐹𝑤 =0) omhoog gehouden
met een spankracht d.m.v. een touw
Fs?
=30°
Fz,x
𝛼
𝛼=15°
Fz=300 N
Fz,y
1. Bereken 𝐹𝑠
𝐹𝑧,𝑥 = 𝐹𝑧 sin 𝛼 = 77,65 𝑁
𝐹𝑧,𝑦 = 𝐹𝑧 cos 𝛼 = 289,8 𝑁
𝐹𝑠,𝑥 = 𝐹𝑧,𝑥 = 77,65 𝑁
𝐹𝑠,𝑥
𝐹𝑠 =
= 90 𝑁
cos 𝛽
2. Is 𝐹𝑁 groter dan 𝐹𝑧,𝑦 , 0, of
kleiner dan 𝐹𝑧,𝑦 ?
Kleiner, want 𝐹𝑠 heeft ook nog een
y-component: 𝐹𝑧,𝑦 = 𝐹𝑁 + 𝐹𝑠,𝑦
§3.5 en §3.6: Eerste en tweede wet van Newton
• 1e wet van Newton: geen resulterende kracht, dan staat een
voorwerp stil, of beweegt het met constante snelheid in
een rechte lijn
Fres = 0  v is constant
(v=0 is ook constant!)
• 2e wet van Newton: Fres=ma
a
Fs
Vaak gebruikt in combinatie met
vergelijkingen/ grafieken voor eenparig
versnelde bewegingen:
Ftouw
a = v/t (raaklijn in v-t grafiek)
F//
Fw
Fres=Ftouw-F// - Fw
Fz
Fres = Fs - Fz
F┴
Fz
§3.7: Derde wet van Newton
3e wet van Newton: als voorwerp A een kracht
uitoefent op voorwerp B, dan oefent B een
tegengestelde en even grote kracht uit op A.
Fn: van grond op blok
.
Z
Fz: van aarde op blok
Fgewicht: van blok op grond
(reactiekracht van Fn)
Fg: van blok op aarde
(reactiekracht van Fz)
Fgew=Fn geldt altijd!
Fz=Fgew geldt alleen
als a=0!
Herhaling hoofdstuk 7: Cirkelbewegingen
v
eenparige cirkelbeweging: de baansnelheid is
constant, ofwel in elk tijdsinterval t legt het
voorwerp een even grote afstand af
Tijd voor 1x rond (360 °):
omlooptijd: 𝑇
Totale afgelegde weg in
1x rond: 2𝜋𝑟
v
𝒓
v
360
Baansnelheid: 𝑣 =
2𝜋𝑟
𝑇
• Frequentie (𝒇) = aantal
omlopen (rondjes) per seconde
1
[𝑓] = Hz
𝑓=
[𝑇] = s
𝑇
• Toerental (n) = aantal omwentelingen (rondjes) per minuut
[𝑛] = RPM (revolutions per minute; rondjes per minuut))
v
§7.2: Middelpuntzoekende kracht
• Een eenparige cirkelbeweging treedt op als er
resulterende kracht op het voorwerp werkt die:
 wijst naar het middelpunt van de baan
 loodrecht op 𝑣 staat
 een grootte heeft gelijk aan
𝑚𝑣 2
.
𝑟
• Deze resulterende kracht (!!) noemen we
de middelpuntzoekende kracht:
𝑚𝑣 2
𝐹𝑚𝑝𝑧 =
𝑟
• In opgaven: vaak combineren van
2𝜋𝑟
vergelijkingen 𝑣 =
en 𝐹𝑚𝑝𝑧
𝑇
• Fmpz is dus geen “echte” kracht maar er is altijd een andere kracht,
of een combi van krachten, die de rol speelt van
middelpuntzoekende kracht. Vaak: Fs(&Fz), Fschuifweerstand, Fgravitatie
§7.3: Gravitatiekracht
• Gravitatiekracht: de kracht die elke twee voorwerpen dankzij
hun massa op elkaar uitoefenen.
m1
Fg
m2
Fg
r
• 𝐹𝑔 =
𝑚 1 𝑚2
𝐺 2 .
𝑟
Waarde van G zie Binas Tabel 7
• Voor satellieten geldt: 𝐹𝑚𝑝𝑧 = 𝐹𝑔 en ook 𝑣 =
2𝜋𝑟
𝑇
- geostationair: T is omlooptijd van aarde!
- polair: baan gaat over beide polen
• Let op (meest gemaakte fouten): neem 𝑟 van middelpunt tot
middelpunt, en vergeet niet km’s om te rekenen!