Raf: 0032-486287070

H16. Goniometrie.
§16.1 Functie voor sinus.
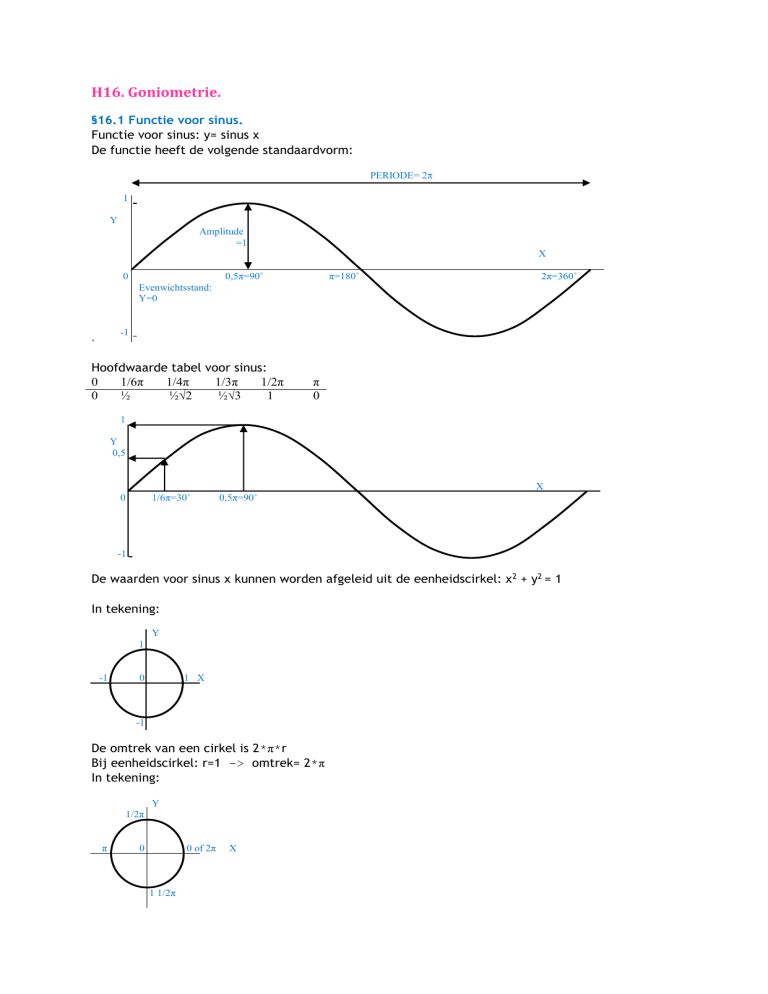
Functie voor sinus: y= sinus x
De functie heeft de volgende standaardvorm:
PERIODE= 2π
1
Y
Amplitude
=1
X
0
0,5π=90˚
π=180˚
2π=360˚
Evenwichtsstand:
Y=0
-1
˚
Hoofdwaarde tabel voor sinus:
0
1/6π
1/4π
1/3π
1/2π
0
½
½√2
½√3
1
π
0
1
Y
0,5
X
0
1/6π=30˚
0,5π=90˚
-1
De waarden voor sinus x kunnen worden afgeleid uit de eenheidscirkel: x2 + y2 = 1
In tekening:
Y
1
-1
0
1 X
-1
De omtrek van een cirkel is 2*π*r
Bij eenheidscirkel: r=1 -> omtrek= 2*π
In tekening:
Y
1/2π
π
0
0 of 2π
1 1/2π
X
De sinus is de verticale beweging (↑) vanuit het midden van de cirkel O.
sinus 45˚= ½ √2
B
45˚
½√2
O
Als je vanuit het midden van de eenheidscirkel O in een hoek van 45˚
naar de eenheidscirkel beweegt, snijd je de cirkel in punt B.
Punt B ligt ½ √2 cm hoger dan punt O: sinus 45˚= ½ √2
Elke π-waarde op de cirkel correspondeert met een hoek vanuit het midden van de cirkel:
Als je vanuit punt A langs de cirkel loopt, kom je uit bij punt B na een afstand van ¼π = 0,79 cm.
sinus (¼π)= sinus 45˚= ½ √2
B
¼ π= 0,79cm
45˚
½√2
O
A
sinus (¼ π)= ½ √2 met Radian
sinus 45˚= ½ √2 met Degree
Van graden naar radialen en omgekeerd: 2π=360˚ en π=180˚
Voorbeeld 1.
a. Bereken sinus 150˚
b. Zet om in radialen.
c. Zet a. en b. in een tekening.
d. Leg uit in woorden.
Antwoord.
a. sinus 150˚= 0,5
b. sinus (150/180) * π= sinus (5/6 * π)= 0,5
c.
5/6 * π= 2,62 cm.
B
0,5cm
150˚
O
1cm
A
d. Als je vanuit het midden van de eenheidscirkel O in een hoek van 150˚
naar de eenheidscirkel beweegt, snijd je de cirkel in punt B.
Punt B ligt 0,5cm hoger dan punt O: sinus 150˚= 0,5
Als je vanuit punt A langs de cirkel loopt,
kom je uit bij punt B na afstand van 5/6 π= 2,62 cm.
§16.2 Functie voor cosinus.
Functie voor cosinus: y= cos x
De functie heeft de volgende standaardvorm:
1
0
1/2π=90˚
π =180˚
1,5π=270˚
2π=360˚
-1
Hoofdwaarde tabel voor cosinus
0
1/6π
1/4π
1/3π
1/2π
1
½*√3 ½√2
½
0
π
-1
De cosinus is de horizontale beweging (→) vanuit het midden van de cirkel.
Elke π-waarde op de cirkel correspondeert met een hoek vanuit het midden van de cirkel:
sinus(1/3π)= sinus 60˚= ½
B
1/3π= 1,05cm.
O
60˚
½
A
Als je vanuit het midden van de eenheidscirkel O in een hoek van 60˚
naar de eenheidscirkel beweegt, snijd je de cirkel in punt B.
Punt B ligt een ½cm rechts van punt O: sinus 60˚= ½
Als je vanuit punt A langs de cirkel loopt, kom je uit bij punt B
na een afstand van 1/3π= 1,05cm: sinus(1/3π)= ½
Voorbeeld 2.
a. Bereken cosinus 180˚
b. Zet om in radialen.
c. Zet a. en b. in een tekening.
d. Leg uit in woorden.
Antwoord.
a. cosinus 180˚= -1
b. cosinus (180/180) * π= cosinus ( π)= -1
c.
π= 3,14 cm.
B
-1
180˚
O
A
d. Als je vanuit het midden van de
eenheidscirkel O in een hoek van 180˚
naar de eenheidscirkel beweegt,
snijd je de cirkel in punt B.
Punt B ligt 1cm links van punt O:
cosinus 180˚= -1
Als je vanuit punt A langs de cirkel loopt,
kom je uit bij punt B na een afstand
van π= 3,14cm.
§16.3 Rekenregels bij sinus.
2 goede oplossingen per periode.
Bij sinus:
spiegelen met half π: a=goed en dus ook a’, bijv. 1/4 π en dus ook 3/4 π
of met anderhalf π: b=goed en dus ook b’, bijv. 1,1π en dus ook 1,9π
1
b
b’
1,5π
0
a
0,5π
a’
-1
Bij cosinus:
spiegelen met π: a=goed en dus ook a’, bijv. 1/2 π en dus ook 1 1/2 π
1
0
a
π
a’
-1
NB: Periode niet altijd gelijk aan 2π
Periode formule: 2 goede oplossingen per elke volgende periode.
sin t= sin(t+2π)= sin(t+2kπ) met k= hele getallen
cos t= cos(t+2π)= cos(t+2kπ)
1
0
-1
NB: Periode niet altijd gelijk aan 2π
Voorbeeld 3.
sin(x)= ½
a. Geef 4 goede oplossingen.
b. Zet de 4 oplossingen in een tekening.
c. Zet 2 goede oplossingen in de eenheidscirkel.
Antwoord.
a. sin-1(0,5)= 0,5235: 1/6π, 5/6π, 2 1/6π, 2 5/6π.
b.
1
0
1/6π
5/6π
2 1/6π
2 5/6π
-1
c.
sinus 1/6π= ½ (zie tekening A)
Er is een ander punt dat ook een verticale beweging heeft van ½ (Zie tekening B).
Tekening A:
Tekening B:
5/6 π
B
1/6 π
½
½
½
A
A
Voorbeeld 4.
cos(x)= ½
a. Geef 4 goede oplossingen.
b. Zet de 4 oplossingen in een tekening.
c. Zet 2 goede oplossingen in de eenheidscirkel.
Antwoord.
a. 1/3π, 1 2/3π, 2 1/3π, 3 2/3π.
b.
1
0
1/3π
1 2/3π
2π
2 1/3π
3 2/3π
-1
c.
cosinus 1/3π= ½ (zie tekening A)
Er is een ander punt dat ook een horizontale beweging heeft van ½ (zie tekening B).
Tekening A:
Tekening B:
B
1/2
1/3π
0
A
0
A
1 2/3π
Voorbeeld 5.
sin(2x)= ½
a. Geef alle goede oplossingen.
b. Zet de oplossingen in een tekening voor Domein [0, 4 π].
Antwoord.
sin(1/6π)= ½ en sin(5/6π)= ½
2x= 1/6π + 2kπ en 2x= 5/6π + 2kπ ->
x= 1/12π + kπ en x= 5/12π + kπ
Merk op: Periode is nu 1π
b.
1/4π
1
0,5
0
1/12π 5/12π
π
2π
3π
4π
-1
3/4π
Voorbeeld 6.
sin(½x)= ½
a. Geef alle goede oplossingen.
b. Zet de oplossingen in een tekening voor Domein [0, 4π].
Antwoord.
sin(1/6π)= ½ en sin(5/6π)= ½
½x= 1/6π + 2kπ en ½x= 5/6π + 2kπ ->
x= 1/3 π + 4kπ en x= 1 2/3π + 4kπ
Merk op: Periode is nu 4π
b.
1
π
0,5
2π
0
1/3π
4π
1 2/3π
-1
3π
kwadratenformule
sin2t + cos2t= 1
1
½√2
cos x
0
sin z
-1
Bij snijpunten y:
02 + 12= 1
Bij snijpunten functies: ( ½√2 )2 + ( ½√2 )2= 1
Ook geldt sin2(at+b) + cos2(at+b)= 1
Verdubbelingsformules.
sin(2t)= 2 * cos t * sin t
cos(2t)= cos2t – sin2t
cos(2t)= 2cos2t – 1
cos(2t)= 1 – 2 * sin2t
§16.4 Afgeleide en integralen.
Afgeleiden:
y= sin x ->
y´= cos x
1
y= sin x
0
-1
MAX.
1 stijging
y'= cos x
0
Δ=0
Δ=0
-1
MAX daling
y= cos x ->
y´= -sin x
1
y= cos x
0
-1
1
MAX stijging
y= -sin x
Δ=0
0
Δ=0
-1
MAX daling
Integralen:
y= sin x ->
F= -cos x + c
y= cos x ->
F= sin x + c
§16.5 Sinus en cosinus in een rechthoekige driehoek.
We hebben gezien dat in een eenheidscirkel de cosinus de verandering geeft
langs de x-as en de sinus de verandering langs de y-as
In tekening:
sin x
cos x
Je kan de driehoek uit de tekening halen en dan gelden de volgende regels:
c
b
α
a
cos α= a/c
sin α= b/c
tan α= b/a
NB: In eenheidscirkel c=r=1 >
cos α= a
sin α= b
Voorbeeld 7.
Een man staat 30 meter voor een toren.
De hoek van de man met de toren is 60˚.
Hoe hoog is de toren.
Antwoord.
Data in een tekening:
c
b
cos α= a/c
cos 60˚= 0,5
30/c= 0,5 -> c= 60
sin 60˚= 0,866
b/60= 0,866 -> b= 51,96
☺
60˚
30 meter
Check:
tan 60˚= 1,73
51,96/30= 1,73
§16.6 Transformatie van sinusfuncties.
§16.6.1 Een functie naar rechts schuiven.
Je kan een functie naar rechts schuiven.
Algemene vorm: y= f(x) -> f(x–c1)
Als je c1 naar rechts wil:
y= sin x ->
y= sin (x–c1)
Voorbeeld 8.
y= sin x
Verschuif de functie π naar rechts.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin (x- π)
1
Y
0
X
π
-1
§16.16.2 Een functie omhoog schuiven.
Je kan een functie omhoog schuiven.
Algemene vorm: y= f(x) -> f(x) + c2
Als je c2 omhoog wil:
y= sin x ->
y= sin x + c2
Voorbeeld 9.
y= sin x ->
Verschuif de functie 1 naar omhoog.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin x + 1
1
Y
0
-1
X
§16.6.3 Een functie met een factor vergroten.
Je kan alle y-waarden met een factor c3 vergroten.
Algemene vorm: y= f(x) -> y= c3 * f(x)
y= sin x ->
y= c3 * (sin x)
= amplitude verandert met factor c3.
Voorbeeld 10.
y= sin x ->
Vergroot alle y-waarden met een factor 2.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= 2 * (sin x)
1
Y
0
X
-1
§16.6.4 De afstand tot de y-as met een factor vergroten.
Je kan voor elke y-waarde de afstand tot de y-as met een factor c4 vergroten.
Algemene vorm: y= f(x) -> y= f (1/c4 * x)
y= sin x ->
y= sin (1/c4 * x)
NB:
Je vergroot de periode met factor c4.
sin (2x)= sin (1:½ * x) -> Periode wordt half zo groot (c4=1/2).
sin (½x)= sin (1:2 * x) -> Periode wordt 2x zo groot (c4=2).
NB: 1:½ = 2
Voorbeeld 11.
y= sin x
Halveer de afstand van de y-waarden tot de y-as met een factor 2.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin(2 * x)
1
Y
0
-1
X
§16.6.5 De functie spiegelen in de y-as.
Als c4= -1: alle y-waarden worden gespiegeld in de y-as.
Algemene vorm: y= f(x) -> y= f(-x)
y= sin x ->
y= sin (-x)
Voorbeeld 12.
y= sin x
Spiegel alle y-waarden in de y-as.
Teken de oude functie, bereken en teken de nieuwe functie.
Antwoord.
y= sin(-x)
Y 1
X
0
-1