Document

5
Goniometrie proefwerk 2
110 cm
15 cm
110 cm
15 cm
10 cm
50 cm
1
a
b
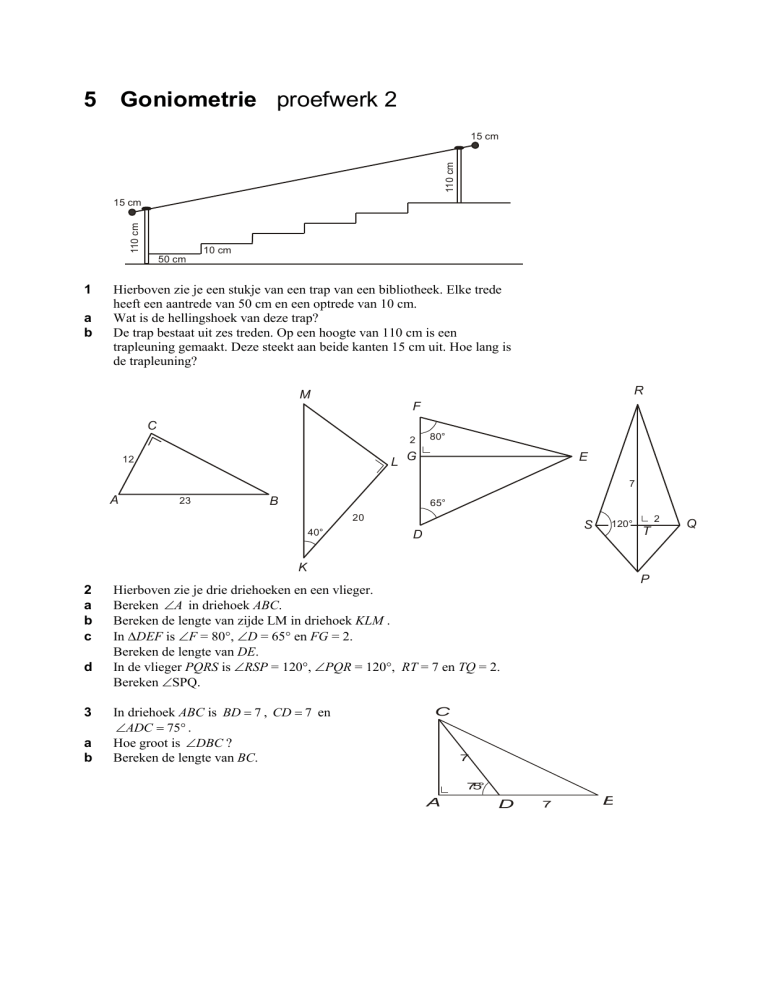
Hierboven zie je een stukje van een trap van een bibliotheek. Elke trede
heeft een aantrede van 50 cm en een optrede van 10 cm.
Wat is de hellingshoek van deze trap?
De trap bestaat uit zes treden. Op een hoogte van 110 cm is een
trapleuning gemaakt. Deze steekt aan beide kanten 15 cm uit. Hoe lang is
de trapleuning?
R
M
F
C
2
80°
L G
12
E
7
A
23
B
65°
20
40°
S
D
120°
2
T
K
2
a
b
c
d
3
a
b
P
Hierboven zie je drie driehoeken en een vlieger.
Bereken A in driehoek ABC.
Bereken de lengte van zijde LM in driehoek KLM .
In DEF is F = 80, D = 65 en FG = 2.
Bereken de lengte van DE.
In de vlieger PQRS is RSP = 120, PQR = 120, RT = 7 en TQ = 2.
Bereken SPQ.
In driehoek ABC is BD  7 , CD  7 en
ADC  75 .
Hoe groot is DBC ?
Bereken de lengte van BC.
C
7
75°
A
D
7
B
Q
180 cm
140 cm
6m
a
a
b
In figuur a hierboven zie je een elastische waslijn die strak gespannen is
tussen de boom en de muur. De boom staat 6 m van de muur. De waslijn
zit bij de boom op een hoogte van 140 cm vast en bij de muur op een
hoogte van 180 cm.
Hoe groot is de stompe hoek die waslijn met de boom maakt?
Bereken de lengte van de waslijn in cm nauwkeurig.
180 cm
4
140 cm
65°
b
c
d
e
*5
a
b
1m
5m
Op 1 m vanaf de boomstam wordt een natte spijkerbroek met behulp van
een hanger aan de waslijn opgehangen. In figuur b hierboven zie je dat de
waslijn nu een hoek van 65º maakt met de boom.
Bereken tot op welke hoogte de waslijn op de plaats waar de broek hangt
is doorgezakt.
Hoe groot is nu de scherpe hoek die de waslijn met de muur maakt?
Hoeveel procent is de waslijn uitgerekt door het gewicht van de
spijkerbroek?
Bij de zandbak staat een speelgoedkist met het deksel
open. Hiernaast zie je hoe de kist staat.
Bereken hoe groot de scherpe hoek is die het deksel
met de muur maakt.
Bereken hoe ver je de kist van de muur af moet
zetten, zodat de scherpe hoek van het deksel van de
kist met de muur 30 is.
muur
30 cm
40 cm
80 cm
50 cm