WI VS 2

WI VS 2
1. Meetkunde (deel 1)
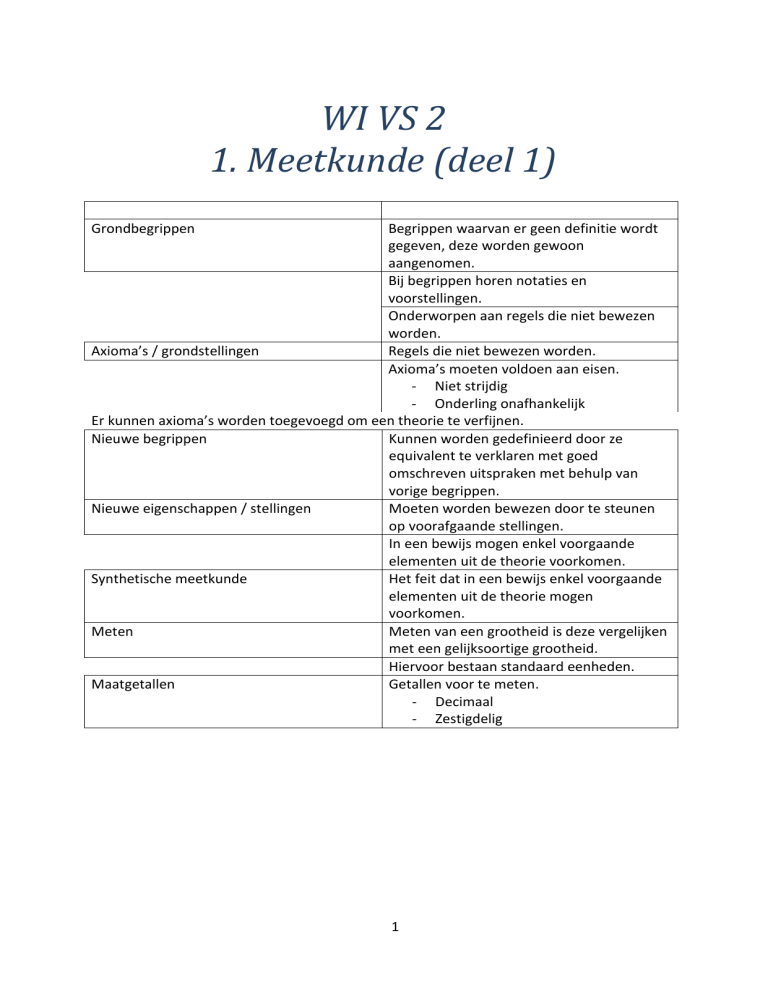
Grondbegrippen
Begrippen waarvan er geen definitie wordt
gegeven, deze worden gewoon
aangenomen.
Bij begrippen horen notaties en
voorstellingen.
Onderworpen aan regels die niet bewezen
worden.
Axioma’s / grondstellingen
Regels die niet bewezen worden.
Axioma’s moeten voldoen aan eisen.
- Niet strijdig
- Onderling onafhankelijk
Er kunnen axioma’s worden toegevoegd om een theorie te verfijnen.
Nieuwe begrippen
Kunnen worden gedefinieerd door ze
equivalent te verklaren met goed
omschreven uitspraken met behulp van
vorige begrippen.
Nieuwe eigenschappen / stellingen
Moeten worden bewezen door te steunen
op voorafgaande stellingen.
In een bewijs mogen enkel voorgaande
elementen uit de theorie voorkomen.
Synthetische meetkunde
Het feit dat in een bewijs enkel voorgaande
elementen uit de theorie mogen
voorkomen.
Meten
Meten van een grootheid is deze vergelijken
met een gelijksoortige grootheid.
Hiervoor bestaan standaard eenheden.
Maatgetallen
Getallen voor te meten.
- Decimaal
- Zestigdelig
1
1.1.
Inleidende begrippen.
1.1.1. Grondbegrippen.
Grondbegrippen in vlakke meetkunde
Relaties tussen grondbegrippen
Het vlak
Een punt
Een rechte
- Vlak
- Punt
- Rechte
- Ligt op
- Gaat door
Negaties van deze relaties worden ook
gebruikt.
Voorgesteld door blad papier of
beeldscherm.
Voorgesteld door een stip.
Notatie: grote letter.
Voorgesteld door lijn getekend met liniaal.
Notatie: kleine letter.
1.1.2. Axioma’s.
Axioma 1: Het vlak is een oneindige verzameling van punten.
Axioma 2: Een rechte is een oneindige echte deelverzameling van het vlak.
Axioma 3: Een rechte is bepaald door twee verschillende punten van het vlak.
Axioma 4: Er bestaan minstens vier punten waarvan er geen drie op een zelfde rechte
liggen.
Axioma 5: Door een punt gaat juist één rechte die evenwijdig is met een gegeven rechte.
Dit is het “parallellenpostulaat van Euclides”.
Concurrente rechten
Collineaire punten
Dualiteit (duale begrippen)
Duality
1
Drie rechten die door het zelfde punt gaan.
Drie punten die op dezelfde rechte liggen.
In de vlakke projectieve meetkunde verwijst
het begrip dualiteit naar het feit dat alle
stellingen een duale versie hebben die
verkregen wordt door de woorden "punt" en
"lijn" en hun acties te verwisselen. Het
begrip is onafhankelijk van elkaar door
Joseph Gergonne en Jean-Victor Poncelet
geïntroduceerd.1
In the geometry of the projective plane,
duality refers to geometric transformations
that replace points by lines and lines by
points while preserving incidence properties
among the transformed objects. The
existence of such transformations leads to a
general principle, that any theorem about
incidences between points and lines in the
projective plane may be transformed into
http://nl.wikipedia.org/wiki/Dualiteit_(meetkunde)
2
Duale begrippen
Snijdende rechten
Parallelle / evenwijdige rechten
Om onderlinge ligging punten en rechten in
het vlak te bestuderen
another theorem about lines and points, by
a substitution of the appropriate words.2
“punt” en “rechte”
“ligt op” en “gaat door”
“collineair” en “concurrent”
Rechten met juist één gemeenschappelijk
punt.
Rechten die niet snijden, dit wil zeggen
rechten die geen enkel of alle punten
gemeenschappelijk hebben.
Zijn we geïnteresseerd in de
gemeenschappelijke elementen van
verzamelingen.
1.1.3. Halfrechte, lijnstuk en afstand. i
Wat is een halfrechte?
Notatie: [AB
3
Voorstelling:
Wat is een lijnstuk?
Notatie: [AB]
Voorstelling:
4
5
Achtergrond:
Meetkundige definitie van lijnstuk.
Lijnstuk kunnen we meten. (def meten zie p1)
Afstand van A tot B = lengte van het lijnstuk.
Notatie: |AB|,
of m.b.v. de afstandsfunctie: d(A,B).
Afstand = positief reëel getal.
Lengte gemeten met lengtematen. |AB| = 4 cm; “4” is het maatgetal, “cm” is de maat.
Hebben twee lijnstukken dezelfde lengte dan noemen we ze “even lang”.
Lijnstuk heeft geen begin- en eindpunt.
2
http://en.wikipedia.org/wiki/Duality_(projective_geometry)
http://www.heiliggraf.be/secundaironderwijs/infovoorELOV/wiskunde_1j/Oefeningen/Hoofdstuk2/Prenten/Oefening3.jpg
4
http://www.heiliggraf.be/secundaironderwijs/infovoorELOV/wiskunde_1j/Oefeningen/Hoofdstuk2/Prenten/Oefening1.jpg
5
http://upload.wikimedia.org/wikipedia/commons/0/0c/Segmento-definicion.png
3
3
1.1.4. Hoek.
Wat is een hoek?
Notatie: Â of BÂC of ∡A
Hoek dikwijls met Griekse letter weergegeven.
6
Voorstelling:
[AB en [AC zijn de benen van de hoek, A is het hoekpunt. We duiden de hoek aan met
een boogje.
Hoek heeft geen beginbeen en geen eindbeen.
i
Zie ook: http://www.heiliggraf.be/secundaironderwijs/infovoorELOV/wiskunde_1j/Oefeningen/Hoofdstuk2/Rechten.htm
6
http://img.sparknotes.com/content/testprep/bookimgs/newsat/0003/angle.gif
4