Opgaves toetsweek 2-2011

Tentamen Natuurkunde voor 6 vwo
Elektriciteit, signaalverwerking, trillingen, golven, cirkelbeweging, modelleren.
Januari 2011
-Vermeld bij alle berekeningen de gegevens en de formules die je gebruikt.
- Laat duidelijk zien hoe je aan het antwoord komt
-Gebruik de juiste afkortingen voor grootheid en eenheid.
-Geef alle eindantwoorden in het juiste aantal significante cijfers
Opgave 1 Sopraansaxofoon
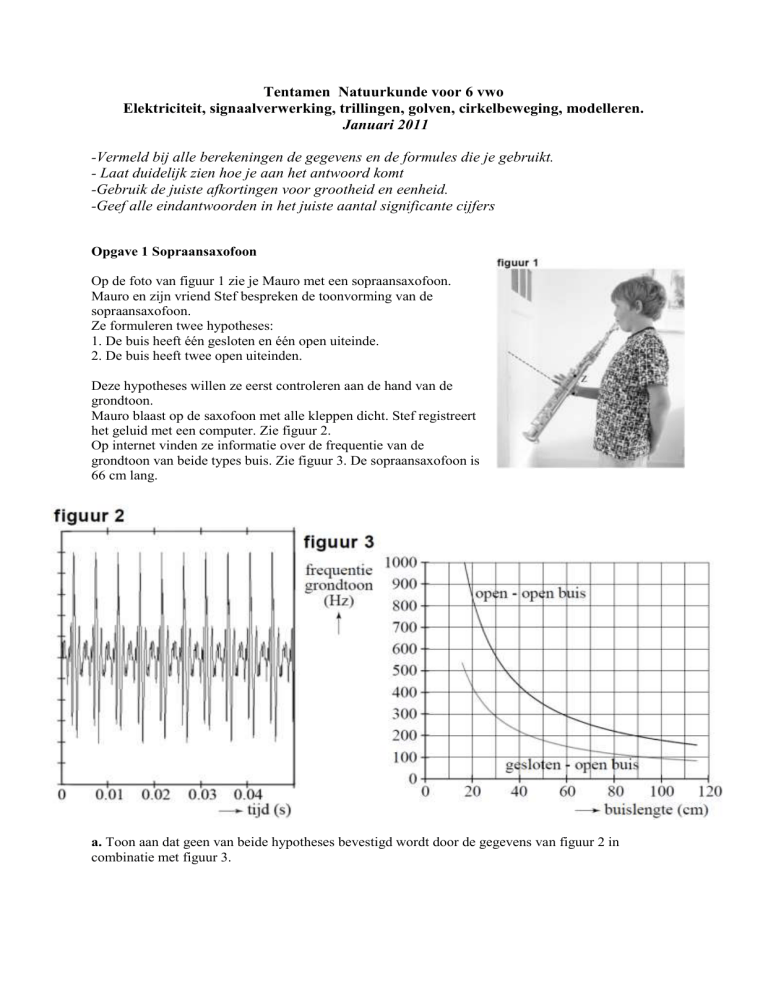
Op de foto van figuur 1 zie je Mauro met een sopraansaxofoon.
Mauro en zijn vriend Stef bespreken de toonvorming van de
sopraansaxofoon.
Ze formuleren twee hypotheses:
1. De buis heeft één gesloten en één open uiteinde.
2. De buis heeft twee open uiteinden.
Deze hypotheses willen ze eerst controleren aan de hand van de
grondtoon.
Mauro blaast op de saxofoon met alle kleppen dicht. Stef registreert
het geluid met een computer. Zie figuur 2.
Op internet vinden ze informatie over de frequentie van de
grondtoon van beide types buis. Zie figuur 3. De sopraansaxofoon is
66 cm lang.
a. Toon aan dat geen van beide hypotheses bevestigd wordt door de gegevens van figuur 2 in
combinatie met figuur 3.
Om nog op een andere manier de hypotheses te testen, kijken Stef en Mauro naar de boventonen. In
figuur 4 zijn de frequenties van de toon van de saxofoon weergegeven.
b. Leg aan de hand van figuur 4 uit dat hypothese 2 het meest gesteund wordt.
Het lijkt er op dat hypothese 2 klopt, maar de grondfrequentie klopt niet.
Daarom gaan Mauro en Stef in de literatuur zoeken hoe het precies zit met de toonvorming van een
sopraansaxofoon. Zij vinden een theorie, die zegt dat een saxofoon een conische buis heeft. Dat wil
zeggen dat de buis een deel van een kegel is. Zie figuur 5. Deze figuur is op schaal.
Door de conische buis is de toonvorming anders dan bij een klarinet of een orgelpijp. Voor de
grondtoon van een conische buis zoals een saxofoon geldt:
  2L
Hierin is:
 λ de golflengte van de grondtoon;
 L de akoestische lengte van de conische buis. Deze kan verkregen worden door de lengte van de
buis te bepalen tot het denkbeeldig punt waar de dikte gelijk wordt aan nul.
c. Laat zien of de metingen van figuur 2 overeenkomen met bovenstaande theorie.
Ondertussen is de saxofoon warmer geworden door het gebruik. De lengte is verwaarloosbaar
toegenomen.
d. Leg uit wat er gebeurt met de frequentie van de grondtoon.
Opgave 2 WaarschuwingsLED
Pierre en Diane maken tijdens een practicum een waarschuwingssysteem waarbij een LED gaat
branden als de temperatuur 20 °C of hoger is.
Op de practicumtafel staan de volgende spullen klaar (zie figuur 1):

 een NTC en een thermometer die zich in het water bevinden;

- en een ampèremeter.
Zij willen eerst een grafiek maken van de weerstand van de NTC tegen de temperatuur. Daarvoor moet
nog een aantal elektrische verbindingen in de practicumopstelling van figuur 1 gemaakt worden. P en
Q zijn de aansluitpunten van de NTC.
a.Teken het schakelschema dat nodig is om de metingen voor deze grafiek te kunnen uitvoeren.
Gebruik hierbij alle onderdelen die in de bovenstaande figuur staan.
In figuur 2 zie je de grafiek die Diane en Pierre hebben gemaakt.
Voor het waarschuwingssysteem beschikken zij verder nog over een variabele weerstand en een LED.
In figuur 3 staat het (I,U)-diagram van de LED.
De LED geeft licht als er een stroom van ten minste 1,0 mA door gaat.
Diane en Pierre bouwen de schakeling van figuur 4.
b. Leg aan de hand van de figuren 2, 3 en 4 uit dat de LED niet brandt bij een lage temperatuur en wel
brandt bij een hoge temperatuur.
c. De variabele weerstand wordt zo ingesteld dat de LED licht geeft bij een temperatuur
van 20 °C en hoger. De spanning van de spanningsbron is 5,0 V.
Bepaal de waarde waarop de variabele weerstand wordt ingesteld.
Opgave 3.
Jan is aan het kogelslingeren. De lengte van zijn
draaipunt tot het midden van de kogel (armen en touw)
is 3 meter. De straal van de cirkel die de kogel doorloopt
is echter maar 2,5 m. De kogel heeft een massa van 2,0
kg. Zie ook de tekening hiernaast. Deze is niet op schaal!
a. Maak een tekening op schaal van alle krachten die op
de kogel werken. Bepaal in deze tekening de kracht in
het touw en de middelpuntzoekende kracht.
b. Bereken de middelpuntzoekende kracht.
c. Bereken de kracht die Jan moet uitoefenen.
d. Bereken de snelheid van de kogel.
Plots breekt het touwtje. Op dat moment was de kogel 85 cm boven de grond.
e. Hoe groot is de horizontale verplaatsing van de kogel als hij de grond raakt? (als je de vorige
opgave niet hebt, mag je uitgaan van v = 7 m/s)
opgave 4. De sleeplift
Een sleeplift trekt skiërs met een kabel de berg op. De skiërs staan daarbij
gewoon op hun ski’s en worden voorgetrokken door een beugel waar ze
tegenaan zitten. Bovengekomen moeten ze van de beugel afstappen. Een
elektronisch oog enkele meters voorbij de afstapplaats slaat alarm als een
skiër per ongeluk niet is afgestapt. De situatie is in de figuur geschetst. De
ijkgrafiek van de lichtsensor is ook weergegeven.
a. Geeft deze sensor een analoog of een digitaal signaal? Leg dit uit.
b. Bepaal het lineaire bereik van de sensor.
c. Bepaal de gevoeligheid van de sensor.
De uitgang van de sensor kan ook voor een digitale verwerking gebruikt worden. De nauwkeurigheid
moet minimaal 10 lux zijn.
d. Bereken het aantal bits van de analoog-digitaal-convertor.
Als een skiër onverhoopt de lichtbundel even onderbreekt, moet er een alarmlampje gaan branden en
tegelijkertijd moet de stroom naar de elektromotor van de lift worden onderbroken. Pas wanneer de
zaak weer veilig is, moet met één druk op de knop de oude situatie weer worden hersteld. In de figuur
is een deel van de schakeling getekend (deze staat ook in de bijlage).
e.
Is het beschreven systeem een meet-, een stuur- of een regelsysteem? Leg je antwoord uit.
De schakeling moet in werking treden als de lichtsterkte kleiner is dan 80 lux.
f. Bepaal de bijbehorende referentiespanning.
g.
Maak de schakeling af, zodat deze voldoet aan de eisen. Gebruik hiervoor de bijlage. Er is
een oplossing met drie extra verwerkers.
Opgave 5. De stuiterbal.
Sommige ballen kunnen extreem goed stuiteren. Als je zo'n bal op een harde
ondergrond laat vallen, stuitert hij weer even hoog op. Model 2 simuleert de valbeweging tot
aan de grond. Bij alle modellen in deze opgave wordt de luchtweerstand buiten beschouwing
gelaten.
regel modelregels
modelregels in Coach startwaarden in Coach
1
a = –g
a = -g
2
dv = a ∙ dt
dv = a * dt
3
v := v + dv
v = v + dv
4
dy = v ∙ dt
dy = v * dt
5
y := y + dy
y = y + dy
6
als y < 0 dan stop als y < 0 dan stop
eindals
7
t := t + dt
g = 9,81
v=0
y = 1,60
t=0
dt = …
'm/s^2
'm/s
'm
's
's
t = t + dt
Model 2
Volgens model 2 bevindt de onderkant van de bal zich op een hoogte van 1,60 m bij het
loslaten.
a. Leg met behulp van het model uit dat tijdens een cyclus van het model de hoogte kleiner
wordt.
Voor een nauwkeurige modelberekening mag dy niet groter zijn dan 1 cm.
b. Welke startwaarde moet je dan voor dt kiezen? Licht je antwoord toe.
c. Mag je de modelregels 1 en 2 verwisselen? Licht je antwoord toe.
d. Mag je de modelregels 2 en 3 verwisselen? Licht je antwoord toe.
Als de bal de grond treft, stuitert hij weer even hard omhoog. De berekeningen in model 2
stoppen echter als de bal de grond treft. Door in regel 6 de uitdrukking ‘stop’ te vervangen
door een andere uitdrukking, simuleert het model dat de bal weer omhoog stuitert.
e. Noteer de nieuwe modelregel 6.
Gooi je zo’n stuiterbal met een snelheid van 2,0 m/s in horizontale richting weg, dan is de
beweging van de bal een horizontale worp. Je kunt die beweging in een model beschrijven
door aan het oorspronkelijke model 2 een modelregel toe te voegen. Het model simuleert de
beweging tot de bal de grond treft.
f. Noteer de modelregel en de bijbehorende startwaarden.
Bijlage.
Opgave 3
Naam……………………………………………