KeCo-opgaven mechanica (arbeid en energie) − HAVO4

KeCo-opgaven mechanica (arbeid en energie) − HAVO4
1
KeCo-opgaven mechanica (arbeid en energie) − HAVO4
M.24.
Een bepaald type waterpomp is in staat om in redelijk korte tijd 30 liter water omhoog
te pompen over een hoogteverschil van 6,2 m.
Bereken de hoeveelheid arbeid die verricht wordt door de pompkracht.
De arbeid kan berekend worden m.b.v. de volgende formule als de kracht en de
verplaatsing in dezelfde richting staan (wat hier het geval is):
W = F ⋅s
De pompkracht is gelijk aan de zwaartekracht die werkt op 30 liter water. Om de
zwaartekracht te kunnen berekenen, dient eerst de massa van 30 liter water
bekend te zijn. Deze kan berekend worden m.b.v. de dichtheid:
m = ρ ⋅V
m = 0,998 ⋅103 ⋅ 30 ⋅10 −3 = 29,9 kg
Fz = m ⋅ g
Fz = 29,9 ⋅ 9,81 = 293,7 N
De pompkracht is dus gelijk aan de zwaartekracht. De arbeid kan dan berekend
worden:
W = F ⋅s
W = 293,7 ⋅ 6,2 = 1,8 ⋅103 J
M.24.
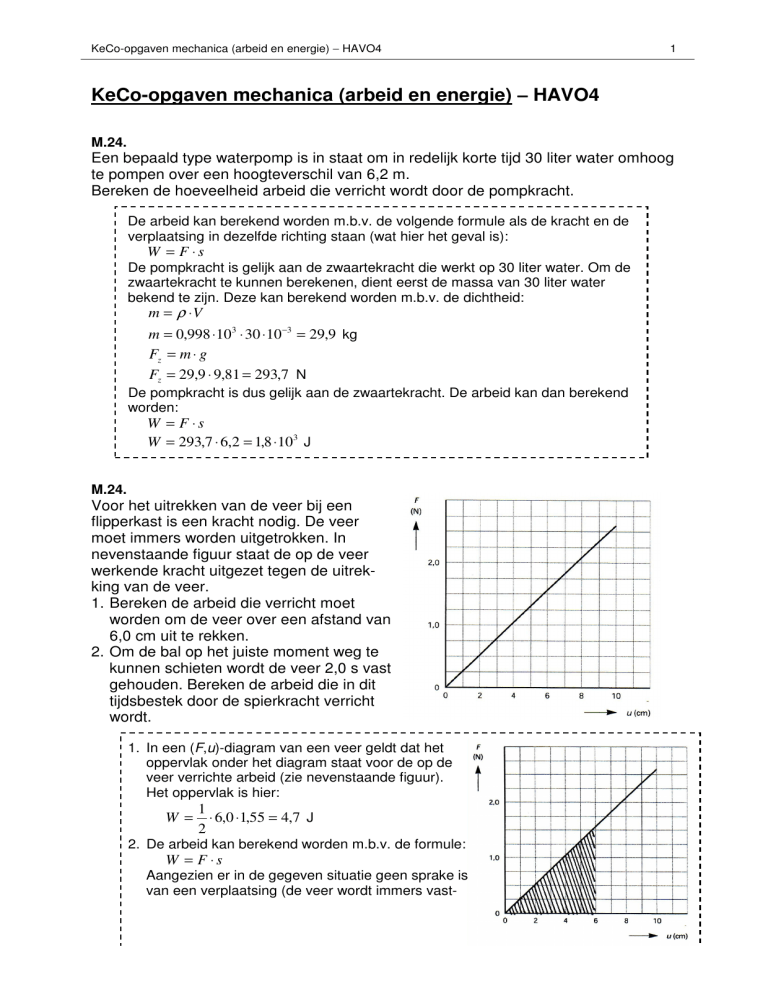
Voor het uitrekken van de veer bij een
flipperkast is een kracht nodig. De veer
moet immers worden uitgetrokken. In
nevenstaande figuur staat de op de veer
werkende kracht uitgezet tegen de uitrekking van de veer.
1. Bereken de arbeid die verricht moet
worden om de veer over een afstand van
6,0 cm uit te rekken.
2. Om de bal op het juiste moment weg te
kunnen schieten wordt de veer 2,0 s vast
gehouden. Bereken de arbeid die in dit
tijdsbestek door de spierkracht verricht
wordt.
1. In een (F,u)-diagram van een veer geldt dat het
oppervlak onder het diagram staat voor de op de
veer verrichte arbeid (zie nevenstaande figuur).
Het oppervlak is hier:
W=
1
⋅ 6,0 ⋅1,55 = 4,7 J
2
2. De arbeid kan berekend worden m.b.v. de formule:
W = F ⋅s
Aangezien er in de gegeven situatie geen sprake is
van een verplaatsing (de veer wordt immers vast-
KeCo-opgaven mechanica (arbeid en energie) − HAVO4
2
gehouden), is er ook geen sprake van arbeid.
Dus geldt: W = 0 J
M.26.
1. Van welke vorm van energie is er sprake als een voorwerp een snelheid heeft.
2. Leid af hoe de formule voor de zwaarte-energie ( E z = m ⋅ g ⋅ h ) kan
worden afgeleid uit de formule voor arbeid ( W = F ⋅ s ).
3. Geef de formule voor de veerenergie. Geef ook een symboolverklaring.
4. Een massa die bevestigd is aan een koord, vormt een slinger.
Zie nevenstaande figuur. De slinger is in beweging. Positie A wordt
ook wel de evenwichtsstand van de slinger genoemd en positie B
heet een uiterste stand (amplitudo).
Geef aan welke energievormen er gelden in respectievelijk de posities
A en B.
5. Geef commentaar op de volgende bewering:
“Als er sprake is van wrijving, is er sprake van energieverlies en kan
de wet van behoud van energie dus niet worden toegepast.”
B
A
1. Als een voorwerp in beweging is, is er sprake van kinetische energie.
2. Als een voorwerp valt, werkt er op dat voorwerp uitsluitend de zwaartekracht
(als wrijvingskrachten verwaarloosd worden). De verplaatsing van een vallend
voorwerp kan ook de hoogte worden genoemd. Dus geldt:
W = F ⋅ s met F = Fz = m ⋅ g
s=h
Dit leidt tot de formule voor de zwaarte-energie: E z = m ⋅ g ⋅ h
3. De formule voor de veerenergie luidt: Ev =
1
⋅C ⋅u2
2
In deze formule geldt: Ev = veerenergie (in J)
C = veerconstante (in N/m)
u = uitrekking (in m)
4. In punt A is de slinger in beweging. Er is hier sprake van de maximale
snelheid en de hoogte van de slingerende bol kan hier 0 worden gesteld. In
punt A bezit de slinger dus kinetische energie. In punt B staat de slinger een
moment stil (dit is het omkeerpunt), terwijl de slingerende bol hier wel een
hoogte heeft. In punt B bezit de slinger dus zwaarte-energie.
5. De wet van behoud van energie zegt dat de totale hoeveelheid energie in een
systeem altijd gelijk blijft. Aangezien energieverlies (of warmte of arbeid
verricht door de wrijvingskracht) ook een vorm van energie is, blijft de wet van
behoud van energie opgaan.
M.27.
Jaap gaat voetballen. Op een gegeven ogenblik trapt Jaap de bal (m = 320 g) met een
snelheid van 9,5 m/s in een schuine richting omhoog. De bal belandt op het dak van een
garage op een hoogte van 2,7 m.
1. Bereken de snelheid waarmee de bal op het dak terecht komt.
Jaap klimt op het dak van de garage om de bal te pakken. Uit woede schiet hij de bal
vertikaal omhoog met een beginsnelheid van 12,6 m/s.
2. Bereken het hoogste punt dat de bal zal bereiken (t.o.v. de grond).
KeCo-opgaven mechanica (arbeid en energie) − HAVO4
3
1. De situatie is schematisch weergegeven
in nevenstaande figuur. In deze situatie
geldt de wet van behoud van energie:
Etot , A = Etot ,B
In punt A bezit de bal uitsluitend kinetisch energie, terwijl de bal in punt B
zowel kinetische als zwaarte-energie
bezit:
Ek , A = Ek , B + E z , B
1
1
2
2
⋅ m ⋅ v A = ⋅ m ⋅ vB + m ⋅ g ⋅ hB
2
2
1 2 1 2
⋅ v A = ⋅ vB + g ⋅ hB (de massa m kan worden weg gedeeld)
2
2
1
1 2
2
⋅ (9,5) = ⋅ vB + 9,81 ⋅ 2,7 → vB = 6,1 m/s
2
2
2. De situatie is schematisch weergegeven in nevenstaande
figuur. In deze situatie geldt de wet van behoud van energie:
Etot , A = Etot ,B
In punt A bezit de bal uitsluitend kinetisch energie, terwijl
de bal in punt B uitsluitend zwaarte-energie bezit:
Ek , A = E z , B
1
2
⋅ m ⋅ v A = m ⋅ g ⋅ hB
2
1 2
⋅ v A = g ⋅ hB (de massa m kan worden weg gedeeld)
2
1
2
⋅ (12,6 ) = 9,81 ⋅ hB → hB = 8,1 m
2
M.27.
Een kogel wordt met een beginsnelheid van 60,0 m/s vertikaal omhoog geschoten en bereikt
hierbij een hoogte van 110 m. De massa van de kogel bedraagt 2,20 kg. Bereken de
gemiddelde grootte van de wrijvingskracht die op de kogel werkt gedurende de beweging
naar boven.
De situatie is schematisch weergegeven in nevenstaande
figuur. In deze situatie geldt de wet van behoud van energie:
Etot , A = Etot ,B
In punt A bezit de bal uitsluitend kinetisch energie, terwijl
de bal in punt B uitsluitend zwaarte-energie bezit. Onderweg
van A naar B verliest de bal een hoeveelheid energie. Dit is
arbeid verricht door de wrijvingskracht
Ek , A = E z ,B + Ww
1
2
⋅ m ⋅ v A = m ⋅ g ⋅ hB + Fw ⋅ h
2
1
2
⋅ 2,20 ⋅ (60,0 ) = 2,20 ⋅ 9,81 ⋅110 + Fw ⋅110
2
→
Fw = 14,4 N
KeCo-opgaven mechanica (arbeid en energie) − HAVO4
M.28.
Een blok met een massa van 250 gram
bevindt zich in een punt A op een hellend vlak.
De snelheid van het blok in dit punt bedraagt
1,8 m/s. Het blok glijdt, onder invloed van de
zwaartekracht, langs de helling naar beneden
en bereikt op een gegeven ogenblik punt B.
De afstand AB bedraagt 4,0 m. Verder werkt
Er op het blok een constante wrijvingskracht
van 0,66 N.
Bereken de snelheid waarmee het blok punt B bereikt.
Deze opgave dient opgelost te worden met behulp van de wet van arbeid en
kinetische energie. Deze luidt:
∑W = ∆E
k
(de som van alle arbeid is gelijk aan de verandering in kinetische energie)
In onderstaande figuur zijn de krachten getekend die op het blok werken: de
zwaartekracht, de normaalkracht en de wrijvingskracht. De arbeid van al deze
krachten kan berekend worden met behulp van de formule:
W = F ⋅ s ⋅ cos α
Voor de zwaartekracht geldt:
Wz = Fz ⋅ s ⋅ cos α
Wz = m ⋅ g ⋅ s ⋅ cos α
Wz = 0,250 ⋅ 9,81 ⋅ 4,0 ⋅ cos(60°) = 4,91 J
Voor de normaalkracht geldt:
Wn = Fn ⋅ s ⋅ cos α
Wn = Fn ⋅ 4,0 ⋅ cos(90°) = 0 J
Voor de wrijvingskracht geldt:
Ww = Fw ⋅ s ⋅ cos α
Ww = 0,66 ⋅ 4,0 ⋅ cos(180°) = −2,64 J
De som van alle arbeid wordt berekend door alle arbeid bij elkaar op te tellen:
∑W = W + W + W
∑W = 4,91 + 0 − 2,64 = 2,27 J
z
n
w
Vervolgens kan de wet van arbeid en kinetische energie worden toegepast:
∑W = ∆E
1
∑W = 2 ⋅ m ⋅ v
k
1
2
− ⋅ m ⋅ vA
2
1
1
2
2
2,27 = ⋅ 0,250 ⋅ vB − ⋅ 0,250 ⋅ (1,8)
2
2
2
2,27 = 0,125 ⋅ vB − 0,405
2
2
B
0,125 ⋅ vB = 2,675
→
vB =
2,675
= 4,6 m/s
0,125
M.29.
Een bepaald type hijskraan is in staat een last van 1400 kg in een tijdsbestek van 15,5 s op
te hijsen over een afstand van 58,0 m. Dit ophijsen gebeurt met een constante snelheid.
4
KeCo-opgaven mechanica (arbeid en energie) − HAVO4
5
Bekend is dat het rendement van het hijsproces 67,0% bedraagt. Bereken, via het
nadrukkelijk toepassen van de systematische probleemaanpak, het door de hijskraan
opgenomen vermogen. Geef het antwoord in het juiste aantal significante cijfers.
De kracht waarmee de last wordt opgehesen, de hijskracht Fhijs, is gelijk aan de
zwaartekracht Fz. Het ophijsen gebeurt immers met een constante snelheid. Er
geldt:
Fhijs = Fz
Fhijs = m ⋅ g = 1400 ⋅ 9,81 = 1,37 ⋅104 N
De arbeid die door de hijskracht verricht wordt kan berekend worden met de
formule:
W = Fhijs ⋅ s
W = 1,37 ⋅10 4 ⋅ 58,0 = 7,97 ⋅105 J
Het vermogen dat geleverd wordt door de hijskraan bedraagt:
W
t
7,97 ⋅105
P=
= 5,14 ⋅104 W
15,5
P=
Dit vermogen is het nuttige vermogen van de hijskraan. Het, door de hijskraan,
opgenomen vermogen kan berekend worden met de formule voor het rendement:
η=
Pnut
⋅100%
Pin
67,0% =
5,14 ⋅10 4
⋅100%
Pin
→
Pin =
5,14 ⋅104
= 7,67 ⋅104 W
0,670