Document

Kenmerk: EWI07/TW/SK/007/DM
Datum:
19 juli 2017
Tentamen Statistiek I (153004) voor BK, BSK en GZW
Vrijdag 2 februari 2007, 9.00-12.00 uur
Dit tentamen bestaat uit 7 opgaven. Het formuleblad en 4 tabellen zijn separaat toegevoegd.
Gebruik van een rekenmachine is toegestaan.
Vermeld je naam, studentnummer en studierichting op tentamenbriefje en werk.
Geef bij beantwoording kort maar duidelijk aan hoe je aan het antwoord komt.
Opgave 1 ( Bedieningsduren helpdeskklanten)
In een onderzoek naar de effectiviteit van een helpdesk werden onder meer de
bedieningsduren van klanten, die de helpdesk een probleem voorlegden, onderzocht.
Hieronder staan de bedieningsduren (in minuten) in een steekproef van 42 klanten,
gerangschikt van klein naar groot gemeten.
0.20
1.80
2.24
3.10
5.76
0.62
1.85
2.26
3.34
6.44
0.63
1.86
2.29
3.66
1.02
1.91
2.37
3.69
1.08
1.93
2.41
3.81
1.23
1.99
2.42
3.98
1.23
2.10
2.49
4.52
1.24
2.11
2.57
4.67
1.38
2.16
2.81
4.95
1.45
2.21
2.94
5.22
Deze meetgegevens worden als volgt samengevat:
Het steekproefgemiddelde is 2.570 en
de steekproefstandaardafwijking is 1.421
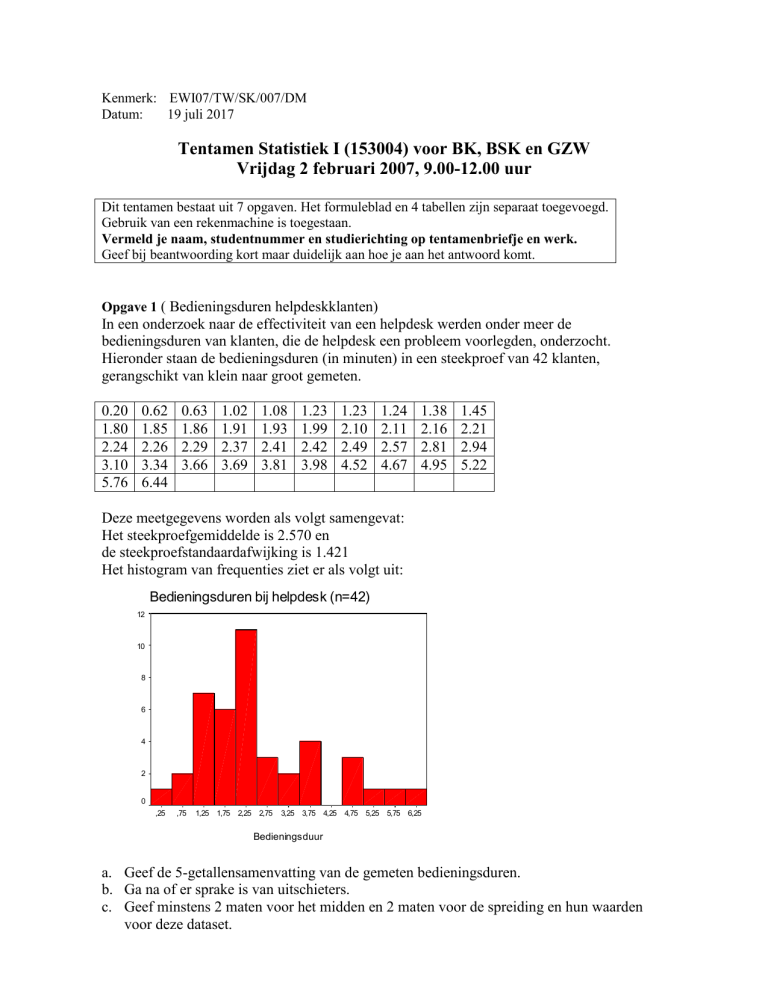
Het histogram van frequenties ziet er als volgt uit:
Bedieningsduren bij helpdesk (n=42)
12
10
Frequentie
8
6
4
2
0
,25
,75
1,25 1,75 2,25 2,75
3,25 3,75 4,25 4,75 5,25 5,75 6,25
Bedieningsduur
a. Geef de 5-getallensamenvatting van de gemeten bedieningsduren.
b. Ga na of er sprake is van uitschieters.
c. Geef minstens 2 maten voor het midden en 2 maten voor de spreiding en hun waarden
voor deze dataset.
d. Wat is het verschil tussen de waarden voor de mediaan en steekproefgemiddelde en hoe
kun je dit verschil verklaren aan de hand van het histogram?
e. Als gevraagd wordt om een betrouwbaarheidsinterval te bepalen voor de verwachte
bedieningsduur van een willekeurige klant, kies je dan voor de z-procedure of de tprocedure? Motiveer uw antwoord.
f. Om toetsen en betrouwbaarheidsintervallen m.b.t. de verwachte waarde te bepalen wordt
veelal uitgegaan van normale verdeling.
1. Is normaliteit voor de bedieningsduren een redelijke veronderstelling? Waarom (niet)?
2. Kunnen we de z- of de t-procedure in dit geval toepassen? Waarom (niet)?
Opgave 2
Bij een benzinestation tankt 40% van de klanten normaal, 35% super een 25% superplus. Van de
mensen die normale benzine tanken moet 30% minstens € 50 betalen. Van de mensen die super
tanken, moet 50% minstens € 50 betalen. En van de mensen die superplus tanken, moet 60% minstens
€ 50 betalen. (Andere brandstoffen worden bij dit benzinestation niet verkocht)
Beantwoord de volgende vragen en geef een duidelijke toelichting op je berekening (met behulp van
een kansboom of door het toepassen van de kansregels).
a. Wat is de kans dat de eerstvolgende klant minstens € 50 moet betalen?
b. De volgende klant blijkt meer dan € 50 te moeten betalen: hoe groot is de kans dat hij superplus
heeft getankt?
Opgave 3
Een studentenvakbond onderzoekt het bestedingspatroon van studenten in Groningen. In een aselecte
steekproef van 30 studenten bleek het gemiddelde bedrag aan uitgaven per maand gelijk aan 691 euro
te zijn bij een steekproefstandaardafwijking van 62 euro.
a. Geef op grond van deze steekproef een 95%-betrouwbaarheidsinterval voor het gemiddelde
bedrag aan uitgaven van alle Groningse studenten.
b. Geef aan of het in a bepaalde interval breder of smaller wordt als
1. Dezelfde steekproefresultaten waren bereikt bij een steekproef van 100 studenten.
2. De betrouwbaarheid groter wordt gekozen.
3. Het gemiddelde in de steekproef 50 euro lager is.
Ga bij de volgende vragen er vanuit dat het bedrag X, dat een willekeurige Groningse student
uitgeeft, normaal verdeeld is met µ = 691 en σ = 62.
c. Geef de kansverdeling van het gemiddelde van 100 willekeurig gekozen Groningse studenten en
bereken de kans dat dit gemiddelde boven 700 euro ligt.
d. Bepaal een interval (a, b) zodanig dat de kans dat het bedrag X tussen a en b ligt 95% is en dat
P(X ≥ b) = 0.025. Waarom is dit interval breder dan het in onderdeel a bepaalde
betrouwbaarheidsinterval?
Opgave 4
Een student moet een scriptie schrijven over de verschillen in gemeentelijke
belastingtarieven. Via veldonderzoek wil hij nagaan of de leges voor
(ver)bouwvergunningen verschillen bij de grotere steden (> 100.000 inwoners) enerzijds en
bij plattelandgemeenten anderzijds. Op basis van een tweetal aselecte steekproeven van 8
steden en 8 plattelandgemeenten tracht hij hierover een uitspraak te doen. De resultaten
hebben betrekking op de leges voor bouwplannen ter waarde van € 20.000 en zijn als volgt
gepresenteerd (in €):
Stad
397 410 428 500 511 519 528 640
platteland 381 402 410 450 457 458 501 560
a. Bereken en vergelijk de steekproefgemiddelden en de steekproefstandaardafwijkingen
van beide steekproeven.
b. Voer een parametrische toets uit waaruit blijkt of het vermoeden, dat de betreffende leges
in steden en plattelandgemeenten verschillen, juist is. Werk de toetsingsprocedure
puntsgewijs uit, door de kritieke waarde bij α = 0.10 te bepalen.
c. We kunnen ook een niet-parametrische (verdelingsvrije) toets uitvoeren op de
meetgegevens in de tabel. Beantwoord hierover de volgende vragen:
1. Hoe heet deze toets?
2. Wanneer valt deze (in het algemeen) te prefereren boven de bij a uitgevoerde toets?
3. Bepaal de waarde van de toetsingsgrootheid.
4. Geef de kansverdeling van de toetsingsgrootheid.
Opgave 5
De onderstaande tabel vermeldt de scores voor twee luistertoetsen Spaans van 20 middelbare
schooldocenten: toets 1 is gehouden vóór en toets 2 ná een intensieve zomercursus in Spaans.
Docent Toets 1 Toets 2 Toets 2- Toets 1
1
30
29
-1
2
28
30
+2
3
31
32
+1
4
26
30
+4
5
20
16
-4
6
30
25
-5
7
34
31
-3
8
15
18
+3
9
28
33
+5
0
20
25
+5
11
30
32
+2
12
29
28
-1
13
31
34
+3
14
29
32
+3
15
34
32
-2
16
20
27
+7
17
26
28
+2
18
25
29
+4
19
31
32
+1
20
29
32
+3
x
s≈
27.3
5.038
28.75
4.745
1.45
3.203
a. Voer de toetsingsprocedure uit om na te gaan of de zomercursus een positief effect heeft op de
luistervaardigheidscores, uitgaande van normale verdeling(en).
b. Er is een niet-parametrische toets als alternatief voor de toets in onderdeel a mogelijk.
1. Geef de naam van deze toets.
2. Geef de kansverdeling van de toetsingsgrootheid.
3. Geef de waarde van de toetsingsgrootheid en bepaal de overschrijdingskans.
4. Hoe luidt de conclusie?
Opgave 6 (Is vruchtensap een remedie tegen Alzheimer?)
In de zomer van 2006 kopten verscheidene bladen dat vruchtensap de kans op Alzheimer met de helft
vermindert. Deze conclusie werd getrokken uit Amerikaans onderzoek onder bejaarde Japanse
immigranten in Seattle. Deze homogene groep is gekozen om andere factoren zo veel mogelijk uit te
sluiten. Aanleiding voor het onderzoek is het vermoeden dat vruchtensap helpt voorkomen dat er
“alzheimerplaques” in de hersenen wordt gevormd. 6 Jaar geleden trof men bij de 1589 bejaarden
geen sporen van Alzheimer aan. Men stelde vast hoeveel glazen vruchtensap per week de
betrokkenen (gemiddeld) dronken en wie er in deze 6 jaar Alzheimer heeft ontwikkeld. We bekijken
de gegevens, waarop de publicaties gebaseerd zijn, nader (uit De Volkskrant van 9 september 2006):
Aantal glazen vruchtensap per week
Minder dan 1 1 of 2 Meer dan 2
positief
30
11
22
Alzheimer screening
negatief
517
246
763
a. Bereken de kansen op Alzheimer in tienden van procenten, afhankelijk van het aantal glazen
vruchtensap per week. Wat is je (voorlopige) conclusie?
b. Bepaal een 95%-betrouwbaarheidsinterval voor het percentage (de fractie) van
Alzheimerpatiënten onder de mensen die minder dan 1 glas vruchtensap drinken.
c. Geef (afgerond in hele procenten):
1. De voorwaardelijke verdeling van het aantal glazen vruchtensap voor de mensen met
Alzheimer.
2. De marginale verdeling van het aantal glazen vruchtensap.
d. Voer een toets uit om te onderzoeken of er een verband bestaat tussen Alzheimer en het aantal
glazen vruchtensap per week. U kunt zich bij de uitwerking van dit onderdeel beperken tot het
geven van de hypothesen, het berekenen van de waarde van de toetsingsgrootheid en de
bijbehorende kritieke waarde en het trekken van een conclusie.
Opgave 7
figuur 1
figuur 2
lineaire regressie van y op x met regressierechte
lineaire regressie van y op x met regressierechte

210
40







180

170

160
50






 



 

 













60












 
 




 
30
 
variabele y
 
190
 

 





 




 





y = 131.01 + 0.69
*x

variabele y


200
20












 






 
 

 

10


 











 



 






0


variabele y = 68.99 + -0.69 * x

-10
70
80
variabele x
90
100
50
60
70
80
variabele x
90
100
figuur 3
figuur 4
lineaire regressie van y op x met regressierechte
lineaire regressie van y op x met regressierechte
variabele y = 100.85 + 0.72 * x
120

120


 




110

115

variabel e y
variabele y
115

 




110




105
105

100


0
variabele y = 122.38 + -0.72 * x
100
10
20
30
variabele x
0
10
20

30
variabele x
De onderstaande vragen hebben betrekking op de 4 figuren hierboven. Van deze figuren
komen de 4 correlatiecoëfficiënten voor in de volgende rij van 7 waarden (in opklimmende
volgorde): -1.45, -0.98, -0.75, 0, +0.75, + 0.98 en +1.45
a.
b.
c.
d.
Geef voor elke figuur de bijbehorende correlatiecoëfficiënt. (Figuur 1: r = …. , etc.)
Geef voor figuur 1 het percentage door het lineaire model verklaarde variantie.
Voorspel voor figuur 1 de waarde van y als x = 85 en als x =120.
Wat is een essentieel verschil tussen de twee berekende voorspellingen in onderdeel c?
-------------------------------------------------------------
Normering:
1
2
3
4
5
6
7
a b c d e f a b a b c d a b c a b a b c d a b c d
3 3 3 2 2 3 4 3 4 3 3 4 3 8 7 8 6 4 4 4 6 4 3 3 3
Totaal
100
Berekening eindcijfer = (aantal punten tentamen + aantal punten SPSS)/12 afgerond
Opmerking: na de herkansing in april vervallen de in het studiejaar 2006/2007 behaalde punten voor
de SPSS-opdrachten.