1 Introductie functies tekenen 2 Veelvoorkomende functies

1
1
Introductie functies tekenen
Functies beschrijven de relatie tussen allerlei variabelen. i.e. hoeveel zwaarder is een persoon naarmate
hij/zij langer is? hoe groeit een bacteriele populatie in de tijd? hoeveel fluorescentie zendt een label
in een cel uit bij beschijning met een laser van welke frequentie? Functies hebben waarschijnlijk een
belangrijke (directe of indirecte) rol in alle onderdelen van de biologie, en ze hebben in ieder geval een
essentiele rol in de cursus systeembiologie waar deze bijspijkercursus op voorbereidt.
Het is daarom belangrijk dat je van de meest voorkomde functies weet hoe ze er ongeveer uit zien (i.e.
rechte lijn, parabool, oscillatie), en dat je ze kan schetsen. Bij dit schetsen komen de meeste onderwerpen terug die we bij de eerdere onderdelen van de bijspijkercursus wiskunde behandeld hebben: waar
snijdt de functie de x-as (i.e. los de funcie op gegeven dat y = 0), waar gaat de functie van stijgend
naar dalend (i.e. waar is de afgeleide van de functie 0), hoe ziet de functie eruit bij lim x → −∞ en
lim x → ∞.
2
Veelvoorkomende functies
We tekenen functies meestal als grafieken. Om dat te doen plotten we de waarde van de variable x op
de x-as en de waarde van de functie f (x) op de y-as. Hieronder laten we een aantal veel voorkomende
grafieken zien die belangrijk zijn in deze cursus.
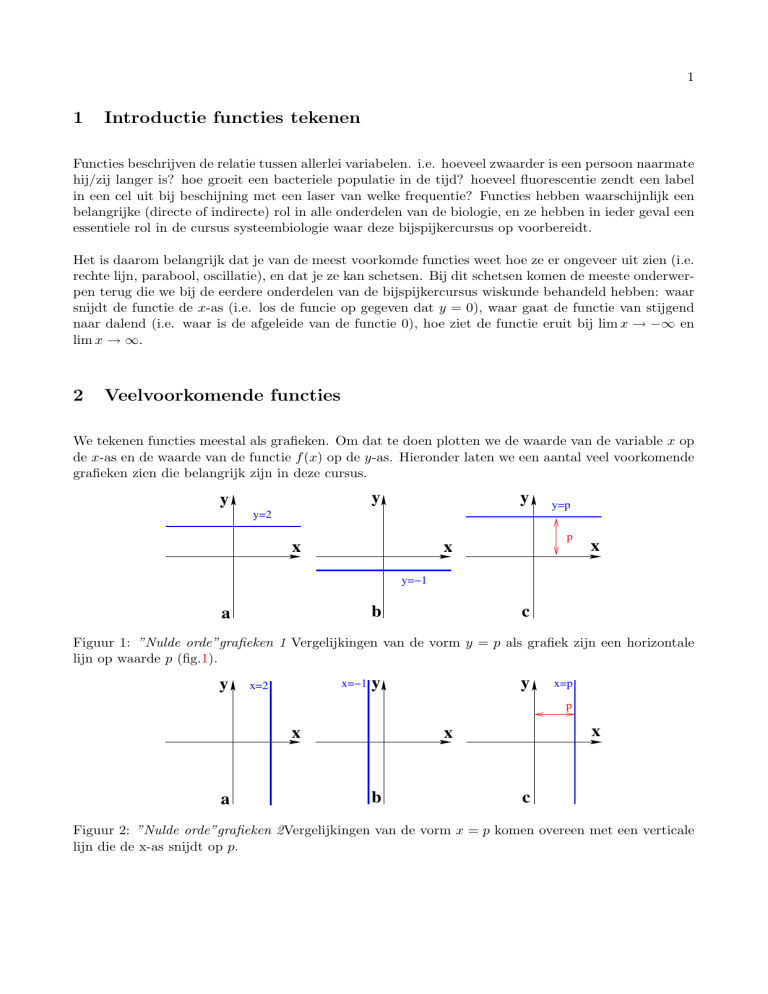
y
y
y=2
y
x
y=p
p
x
x
y=−1
b
a
c
Figuur 1: ”Nulde orde”grafieken 1 Vergelijkingen van de vorm y = p als grafiek zijn een horizontale
lijn op waarde p (fig.1).
y
x=−1
x=2
y
y
x=p
p
x
a
x
x
b
c
Figuur 2: ”Nulde orde”grafieken 2Vergelijkingen van de vorm x = p komen overeen met een verticale
lijn die de x-as snijdt op p.
2
Figuur 3: Lineare grafieken Vergelijkingen van de vorm y = ax + p (lineaire functies) produceren een
rechte lijn met hellingshoek gegeven door de parameter a: hoe groter de absolute waar van a hoe stijler
de hoek (fig.3), een positieve waarde van a betekent dat de grafiek van links naar rechts omhoog loopt,
terwijl een negatieve waarde van a betekent dat de grafiek naar beneden loopt (van links naar rechts).
De parameter p in y = ax + p bepaalt de verschuiving van de grafiek ten opzicht van de x-as en geeft
de plek waar de functie de y-as snijdt. Een positieve p schuift de grafiek naar boven ten opzichte van
de x-as en een negatieve p schuift de grafiek naar beneden ten opzichte van de x-as.
Figuur 4: Kwadratische (twee-orde) grafieken De vergelijking y = ax2 + bx + c beschrijft een parabool,
als a > 0 dan is de parabool een dalparabool en als a < 0 dan is het een dalparabool. Hoe groter
de absolute waarde van a hoe steiler de parabool. De parameter c bepaalt de verschuiving van de
grafiek ten opzicht van de x-as en geeft de plek waar de functie de y-as snijdt. De parameter b
geeft de horizontale verschuiving ten opzchte van de y-as. We kunnen uitrekenen dat de horizontale
b
verschuiving gegeven wordt door − 2a
. We kunnen dit doen door de extreme waarde (maximum
or minimum) van de functie uit te rekenen. Op dit punt is de afgeleide van de functie nul dus
b
(ax2 + bx + c)0 = 2ax + b = 0. De x coordinaat van het extremem is gegeven door xv = − 2a
, oftewel in
b
andere woorden de parabool wordt verschuiven met xv = − 2a van zijn centrale lokatie in de grafiek.
De parabool kan hoogstens twee punten hebben waar hij de x-as snijdt. Deze snijpunten kan je vinden
door middel van de abc-formule. Als deze twee snijpunten (p, q) uitgerekend kunnen worden, kan je
de grafiek makkelijk tekenen met behulp van deze punten. Want in dit geval bevindt het minimum
of het maximum zich altijd in het midden tussen deze twee snijpunten. Wat verder belangrijk is, is
dat als de discriminant D = b2 − 4ac van de abc-formule > 0 dat we dan inderdaad twee snijpunten
met de x-as hebben met de extreme waarde in het midden. Als de D = 0 dan hebben we maar 1 punt
waar de parabool de x-as raakt en dat raakpunt is ook de extreme waarde van de parabool is. Als de
D < 0 dan raakt of snijdt de parabool de x-as niet. Want dan heeft de abc formule geen oplossing
(wortel uit een negatieg getal).
3
y=−x3
y
y
y=x3
y
y=ax3 +bx 2 +cx +d
x
y=a(x−p)(x−q)(x−r)
x
q
p
b
a
x
r
c
Figuur 5: Cubische (derde orde) grafieken Voor een cubische functie van de vorm y = ax3 +bx2 +cx+d
zijn er in het algemeen veel meer mogelijkheden die we hier niet allemaal bespreken. Twee simpele
vormen worden gegeven door de functies y = x3 en y = −x3 afgebeeld in Fig.5a. Van belang voor
een derde orde functie is ten eerste het asymptotische gedrag. Als de cubische term (x3 )vooraf wordt
gegaan door een positieve parameter (bijvoorbeeld 2), dan x → ±∞ dan gaat y naar ∞ en bij
x → ±−∞ gaat y naar −∞. Verder kan een functie van de vorm y = ax3 +bx2 +cx+d tot 3 snijpunten
met de x-as hebben. Deze snijpunten kan je vinden door de vergelijking ax3 + bx2 + cx + d = 0
op te lossen. Ten slotte kan een cubische functie hoogstens twee extremen hebben (1 maximum
en 1 minimum) De extremen zijn punten waar de afgeleide van de functie nul is. De extremen
zijn voor deze functie dus te vinden door het oplossen van de volgende kwadratische vergelijking:
(ax3 + bx2 + cx + d)0 = 3ax2 + 2bx + c = 0. Als de snijpunten met de x-as (p, q, r), de extremen en het
assymptotisch gedrag bekend zijn kan de je functie makkelijk schetsen zoals geillustreerd in Fig.5c.
y
y
x=y 2
x
a
y
y= x
x
x
b
3
y= x
c
Figuur 6: Grafieken van machtsfuncties met machten kleiner dan nul We laten hier twee voorbeelden
van grafieken van machtsfuncties xa met 0 < a < 1 zien. Als 0 < a < 1, dan stijgt de functie langzamer
√
dan de functie y = x en krijg je een afvlakkende curve. Om de functie y = x te tekenen gaan we
eerst eens de functie x = y 2 tekenen. Als we in de functie x = y 2 de x en y omdraaien dat krijgen
we y = x2 . Daarom kan de functie van de functie x = y 2 gevonden worden door de x en y-as van de
parabool y = x2 (zoals in Fig.4a) om te ruilen en dan verkrijgen we de curve zoals je ziet in fig.6a.
√
Gegeven dan dat x = y 2 equivalent is aan y = ± x. Dus het bovenste deel van de curve in fig.6a
√
√
komt overeen met y = x, terwijl de onderste deel van de curve overeenkomt met y = − x. Dus
we hoeven alleen maar het bovenste deel van de curve gegeven door de functie x = y 2 te nemen om
√
√
y = x te verkrijgen. Op vergelijkbare wijze kan je de functie van y = 3 x (Fig.6c) vinden door een
rotatie met 90o van de functie y = x3 zoals gegeven in Fig.5a.
4
y=
y
y
y= 1
x
1 +b
x+a
b
x
y= x+a
1
a
x
y
slope 1
a
x
x
c
b
a
Figuur 7: Grafieken van hyperbolische functies 1 We laten hier voorbeelden zien van grafieken van
1
hyperbolische functies van het type p(x)
q(x) . De grafiek van de functie y = x (Fig.7a) heeft een verticale
1
assymptoot (x = 0) en een horizontale assymptoot (y = 0). De grafiek van de functie y = x+a
+b
1
kan je simpel tekenen door de grafiek van de functie y = x met b in de y (verticale) richting te
verplaatsen en door met −a in de x (horizontale) richting te verplaatsen. In dit geval ligt de verticale
asymptoot (de waarde waarbij x naar ±∞ gaat) op de lijn x = −a, omdat op dit punt de noemer in
1
1
x+a gelijk is aan nul. De horizontale asymptoot van de grafiek van de functie y = x+a + b verplaatst
1
1
zich ook en is y = b. De functies y = x en y = x+a + b worden ook wel hyperbolische functies,
oftewel hyperbolen genoemd. Een andere bekende hyperbolische functies vinden we in de klassieke
x
Michaelis-Menten kinetiek: y = x+a
. Fig.7c laat de grafiek van deze functie zien. Aangezien voor
biologische toepassingen er altijd vanuit gegaan wordt dat x en a niet negatief zijn (x ≥ 0, a > 0),
laten we nu de grafiek alleen maar in het stuk van assenstelsel zien waar x en y groter dan nul zijn.
Je kan zien dat onafhankelijk van de waarde van de parameter a de horizontale asymptoot altijd op
x
= 1. De hellingshoek van deze functie bij x = 0 is gegeven door
y = 1 loopt, aangezien lim x → ∞ x+a
x 0
a
1
0
0
de afgeleide van de functie f (x) = ( x+a
) = (x+a)
2 bij x = 0, wat zcih vertaalt in f (0) = a .
y=
y
1
y= x2
y
1 +b
2 2
x+a
y
x2
y= x2+ a2
1
x
b
x
x
slope=0
c
b
a
Figuur 8: Grafieken van hyperbolische functies 2 In figuur 8a,b laten we vergelijkbare functies zien als
1
1
in Fig.7 maar nu met x tot de tweede macht: y = x12 en y = x2 +a
2 . Je kan zien dat de functie y = x2
een grafiek heeft die veel lijkt op de functie y = x1 maar dat y positief blijft, omdat x2 altijd positief
1
is. Een belangrijk verschil voor de functie y = x2 +a
2 is dat hij niet langer een verticale asymptoot
2
heeft bij x = −a, omdat x altijd positief is en dus nooit gelijk kan zijn aan −a2 . In plaats van een
2
asymptoot heeft ie nu een maximum bij x = 0. De functie y = x2x+a2 (en z’n meer algemene versie
n
y = xnx+an )worden vaak in de biologie gebruikt (o.a. andere voor populatiegroei naar een maximum).
x
De grafiek van deze functie (Fig.8c) heeft een horizontale asymptoot op y = 1 (zoals y = x+a
, maar de
2
x
groeisnelheid van y = x2x+a2 voor kleine waarden van x is langzamer dan voor y = x+a
: de hellingshoek
van de raaklijn bij x = 0 is 0 in plaats van 1/a, hetgeen je kan achterhalen door de afgeleide van deze
functie op x = 0 uit te rekenen.
5
1−
λt
e
λt
e
λ<0
a
t
λ>0
1−
b
−π
t
sin(x)
1
π
−1
c
Figuur 9: Grafieken van exponentiele en trigoniometische functies Ten slotte willen we in fig.9 nog
grafieken laten zien van twee functies die belangrijk zijn voor de systeembiologiecursus: eλt en sin(x).
Het is belangrijk om in te zien dat als t groeit de functie eλt naar nul gaat als λ < 0 en dat het de
functie juist naar oneindig gaat voor λ > 0. De functie sin(x) oscilleert met een periode 2π tussen −1
en +1.
6
3
Tekenen van grafieken
Het tekenen van grafieken is vaak belangrijk, zo ook in de eerstejaars cursus systeembiologie. Veel
van de onderwerpen die we in de bijspijker cursus behandelen zijn nodig om de grafieken van functies
te kunnen tekenen (bijvoorbeeld limieten, differentiren). In de cursus systeembiologie is het nodig
om een grafiek te tekenen van f die afhangt van de variable x (dus f (x)), maar ook afhangt van
constante parameters zoals a, b, c. In de voorbeelden en opgaves behandelen we daarom naast functies
met getallen (i.e. ingevulde parameters) ook het schetsen van functies met parameters.
Hoe teken je nu een grafiek? Er zijn twee manieren mogelijk. Het eerst wat je kan doen, is met een
simpele rekenmachine, of gewoon met hoofdrekenen, een tabelletje te maken door relevante waarden
voor x in te vullen. Als je echter niet weet hoe een functie er ongeveer uit ziet, kan het aardig mis gaan
met deze methoden onder andere wanneer je niet de juiste waarden van x invult. Als er bijvoorbeeld in
1
wel de x waarden -100, -5, -1, 0, 1, 5, 100 in zou vullen zou je zomaar de verticale
de functie y = x−10
asymptoot bij x = 10 kunnen missen! Op dezelfde wijze mis je ook makkelijk andere belangrijke
punten (zoals minima en maxima). Het grootste probleem met deze aanpak, is echter dat je functies
met parameters in plaats van getallen er helemaal niet mee kan schetsen. Terwijl dat wel essentieel is.
Een betere oplossing is dus de zogenaamde analytische aanpak, waarbij je de functie analyseert met
als doel te bepalen waar de functie de x-as en y-as snijdt; of er asymptoten zijn en waar ze liggen; of
er extremen zijn (mimima en maxima) en waar ze liggen.
1. Snijpunten met de x-as vindt je door te stellen f (x) = y = 0 en deze vergelijking op te lossen voor
x (dus bij welke x is f (x) nul).
2. Intersectie punten met de y-as vindt je door x = 0 in te vullen in de functie f (x) en te kijken wat
er uitkomt voor f (x) = y.
Let wel op dat niet alle functies de x- en/of de y-as snijden. Dus als je vergelijking geen oplossing
heeft (zoals wanneer voor de parabool y = ax2 + bx + c de discrimant (D = b2 − 4ac) in de abc formule
kleiner dan nul is) dat snijdt de functie dus de x of y as niet.
3. Horizontale asymptoten vind je met de limieten y = lim x → +∞ en y = lim x → −∞. Er is
sprake van een horizontale asymptoot als de waarde van de limieten een getal is voor lim x → +∞ of
lim x → −∞. Als de functie bij lim x → +∞ of lim x → −∞ zelf naar lim x → +∞ of lim x → −∞ gaat
dan is er geen horizontale asymptoot maar dan weet je wel het gedrag van je functie bij lim x → +∞
of lim x → −∞.
4. Hyperbolische functies van de vorm f (x) = p(x)
q(x) hebben verticale asymptoten als er x waarden zijn
waarvoor q(x) = 0 en f (x) dus naar plus or min oneindig gaat.
Let op dat niet alle functies horizontale en verticale asymptoten hebben.
5. Je kan de locaties (de x-waarden) van de extremen (de minima en maxima) van een functie f (x)
vinden door de afgeleide f 0 (x) te bepalen en dan te achterhalen voor welke waarde van x de afgeleide
voldoet aan f 0 (x) = 0. Als je dan de waarde(n) van x in f (x) invult vindt je de hoogte (y-waarde)
van de maxima en minima.
6. Als je wilt weten of een functie stijgt of daalt als een functie van x voor een bepaald bereik van x
waarden (bijvoorbeeld tussen een minimum en een maximum), dan kan je de afgeleide f 0 (x) voor die
7
x waarde(n) bepalen. Als f 0 (x) > 0 dan stijgt f (x) lokaal als functie van x, en f 0 (x) < 0 betekent dat
f (x) lokaal daalt als functie van x.
y
y=f(x)=
p(x)
q(x)
y−intercept y=f(0)
zeros f(x*)=0
f(x)
horizontal asymptote y=lim
x−>
8
vertical asymptote q(x*)=0
Deze regels kan je samenvatten in de volgende figuur: fig.10.
x
relative extrema df/dx=0
Figuur 10:
Voor alle bovenstaande punten (snijpunten, asymptoten, extremen en afgeleiden) geldt dat ze afhangen
van de parameters. Als de parameters, bekend zijn (zoals in de meeste opgaven) dan zou je de functies
eventueel ook kunnen tekenen met de invullen van x waarde methoden die hieronder staat beschreven.
Maar voor vergelijkingen met parameters zoals a, b of c werkt deze strategie niet, en is het dus van
groot belang bij het schetsen van zo’n functie dat je snijpunten en dergelijke analytisch kan uitrekenen.
Dit is bijvoorbeeld vaak het geval bij de cursus systeembiologie. Daarom is de analytische methode,
de methode waar we de voorkeur aangeven.
4
4.1
Online studiemateriaal
Khan lectures over limieten
De khan lectures leggen goed en rustig uit wat de logica is achter het het tekenen van grafieken aan de
hand van minima, maxima, en snijpunten. Voor Khan lectures over limieten en het gedrag van functies
bij ∞ kan je op de webpagina van de bijspijkercursus wiskunde kijken bij het online lesmateriaal over
limieten van functies.
De volgende links bevatten online lezingen van de Khan acadamy op youtube.
Intuitie voor het achterhalen van maxima en minima uit de hellingshoek (afgeleide): http://www.
youtube.com/watch?feature=player_embedded&v=tpHz0gZfVss
Voorbeeld van het uitrekenen van minimum en maximum op een interval: http://www.youtube.com/
watch?v=gzmSKrwiG3g
8
Tekenenen van een kwadratische functie met behulp van het invullen van getallen (dit raden we dus
niet aan als goede strategie. Zie boven voor een toelichting.) http://www.youtube.com/watch?
feature=player_embedded&v=3a7UbMJpeIM
Een voorbeeld van het tekenen van functies met behulp van de afgeleide http://www.youtube.com/
watch?v=hIgnece9ins (alhoewel de lecture hier verder gaat dan voor ons nodig is, hij achterhaalt ook
of de punten met afgeleide nul, minima of maxima zijn door het analyseren van de tweede afgeleide
(de afgeleide van de afgeleide))
Voorbeeld van hoe een hyperbolische grafiek te tekenen: http://www.youtube.com/watch?v=ReEMqdZEEX0
Nog een voorbeeld van hoe je een hyperbolische functie tekent: http://www.youtube.com/watch?v=
p7ycTWq6BFk
Tekenen van een exponentiele functie (met “teveel” invullen van x-waarden): http://www.youtube.
com/watch?v=9SOSfRNCQZQ
Nog eens tekenen van een exponentiele functie http://www.youtube.com/watch?v=6WMZ7J0wwMI
4.2
DWO en MathAdore
Functies tekenen beslaat vrijwel de hele wiskunde dus op MathAdore kan je bijvoorbeeld eens rondkijken bij “functies en grafieken” en “Differentiaal- en integraalrekening” op hun wiskunde B deel van
de site: http://www.math4all.nl/MathAdore/StartVB.html
Extra opgaves kan je vinden bij het DWO pakket van het Freudenthal instituut. Ga naar http:
//www.fi.uu.nl/dwo/sk, login (als gast). Ga naar module B: Functies, grafieken en inversen, en doe
de activiteiten 1 t/m 5.
5
Opgaves
Voor de volgende functies, bepaal de waarden (en of ze bestaan) van de: snijpunten met de x- en
y-as; de verticale en/or horizontale asymptoot; de extremen (minima en maxima). Schets daarna de
functie.
1. y = 3 − 6x
2. y = x − 3x2
9
3. y = x3 − 5x2
4. y =
4x
x+2
+4
3x
+ 4. Naast het bepalen van de belangrijke punten, bepaal ook hoe de vorm van de
5. y = x+a
grafiek bij x, y ≥ 0 afhangt van de waarde van de parameter a voor relevante a > 0.