Wb 3.6 atoomtheorie - science.uu.nl project csg

Werkblad 3.6: Atoomtheorie
(auteur Leo van Dijk)
Project Moderne Natuurkunde
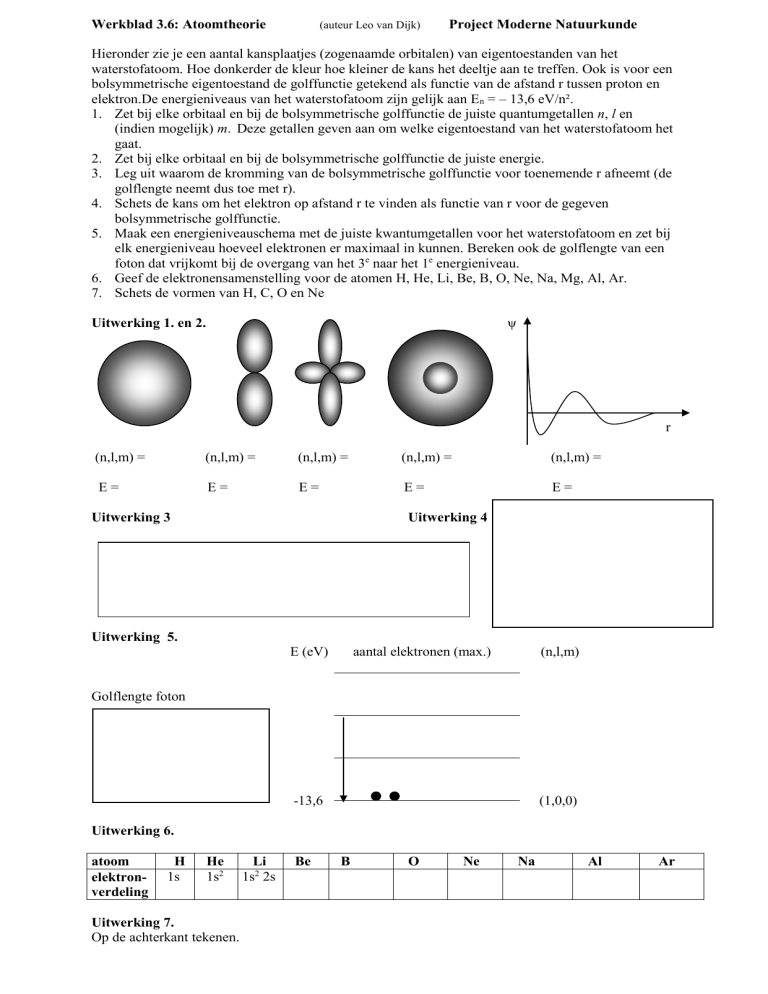
Hieronder zie je een aantal kansplaatjes (zogenaamde orbitalen) van eigentoestanden van het
waterstofatoom. Hoe donkerder de kleur hoe kleiner de kans het deeltje aan te treffen. Ook is voor een
bolsymmetrische eigentoestand de golffunctie getekend als functie van de afstand r tussen proton en
elektron.De energieniveaus van het waterstofatoom zijn gelijk aan En = – 13,6 eV/n².
1. Zet bij elke orbitaal en bij de bolsymmetrische golffunctie de juiste quantumgetallen n, l en
(indien mogelijk) m. Deze getallen geven aan om welke eigentoestand van het waterstofatoom het
gaat.
2. Zet bij elke orbitaal en bij de bolsymmetrische golffunctie de juiste energie.
3. Leg uit waarom de kromming van de bolsymmetrische golffunctie voor toenemende r afneemt (de
golflengte neemt dus toe met r).
4. Schets de kans om het elektron op afstand r te vinden als functie van r voor de gegeven
bolsymmetrische golffunctie.
5. Maak een energieniveauschema met de juiste kwantumgetallen voor het waterstofatoom en zet bij
elk energieniveau hoeveel elektronen er maximaal in kunnen. Bereken ook de golflengte van een
foton dat vrijkomt bij de overgang van het 3e naar het 1e energieniveau.
6. Geef de elektronensamenstelling voor de atomen H, He, Li, Be, B, O, Ne, Na, Mg, Al, Ar.
7. Schets de vormen van H, C, O en Ne
ψ
Uitwerking 1. en 2.
r
(n,l,m) =
(n,l,m) =
(n,l,m) =
(n,l,m) =
(n,l,m) =
E=
E=
E=
E=
E=
Uitwerking 3
Uitwerking 4
Uitwerking 5.
E (eV)
aantal elektronen (max.)
(n,l,m)
Golflengte foton
-13,6
(1,0,0)
Uitwerking 6.
atoom
elektronverdeling
H
1s
He
1s2
Uitwerking 7.
Op de achterkant tekenen.
Li
1s2 2s
Be
B
O
Ne
Na
Al
Ar