PARATE KENNIS & VAARDIGHEDEN WISKUNDE 1STE JAAR
1. TAALVAARDIGHEID BINNEN WISKUNDE
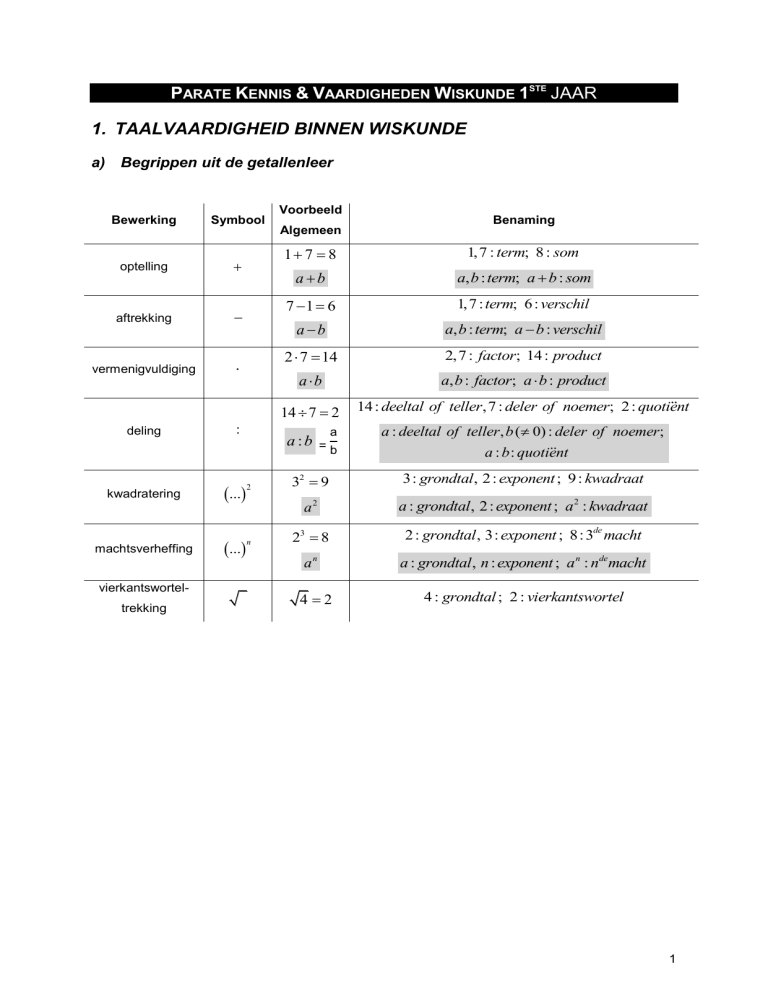
a) Begrippen uit de getallenleer
Bewerking
Symbool
optelling
aftrekking
vermenigvuldiging
deling
kwadratering
machtsverheffing
vierkantsworteltrekking
:
Voorbeeld
Algemeen
1 7 8
1,7 : term; 8 : som
ab
a, b : term; a b : som
7 1 6
1,7 : term; 6 : verschil
a b
a, b : term; a b : verschil
2 7 14
2,7 : factor; 14 : product
a b
a, b : factor; a b : product
14 7 2
14 : deeltal of teller,7 : deler of noemer; 2 : quotient
a :b =
...
2
...
n
Benaming
a : deeltal of teller , b ( 0) : deler of noemer;
a : b : quotient
32 9
3: grondtal , 2 : exponent ; 9 : kwadraat
a2
a : grondtal , 2 : exponent ; a 2 : kwadraat
23 8
2 : grondtal , 3: exponent ; 8: 3de macht
an
a : grondtal , n : exponent ; a n : nde macht
4 2
4 : grondtal ; 2 : vierkantswortel
1
b) Begrippen uit de meetkunde
Meetkundige voorstelling
punt
halfrechte
rechte
lijnstuk
Lees
het punt A
de halfrechte [AB,
A is het grenspunt
de rechte a of de rechte AB
het lijnstuk [AB],
de grenspunten zijn A en B
hoek
de hoek Â
loodrechte stand
rechte a staat loodrecht op rechte b
rechten
evenwijdige rechten,
niet samenvallend
evenwijdige rechten,
samenvallend
in symbolen:
ab
rechte a is evenwijdig met rechte b
in symbolen:
a / /b
a=b
snijdende rechten
a
b
kruisende rechten
a b
2
c) Lengte-, oppervlakte- en volumematen
Lengtematen
km
hm
100m
dam
10m
m
dm
cm
Mm
dm²
cm²
mm²
Oppervlaktematen
km²
ha
hm²
10000m²
a
dam²
100 m²
ca
m²
Volumematen
m3
dm3
cm3
dl cl ml
d) Letters uit het Griekse alfabet
Symbool
Lees
Alfa
Bèta
Gamma
Delta
Pi
3
e)
Instructietaal
Instructie
schets
Betekenis binnen wiskunde
WAT?
Binnen wiskunde betekent schetsen iets in grote lijnen
tekenen om een idee te krijgen van een gegeven
situatie.Om een schets te kunnen maken, maak je gebruik
v n, de gegevens, een definitie, eigensch ppen, …
NAUWKEURIGHEID?
Een schets hoeft helemaal niet nauwkeurig te zijn. Het
geeft jou een eerste indruk.
Voorbeeldopgave
Schets een kubus.
BENODIGDHEDEN?
Om te schetsen volstaat een potlood.
Je hebt geen lat, passer of geodriehoek nodig.
WAT?
Binnen wiskunde betekent tekenen een nauwkeurige
voorstelling of afbeelding maken van een situatie.
teken
NAUWKEURIGHEID?
Afhankelijk van het meetinstrument.
Voorbeelden:
Een lijnstuk op één millimeter nauwkeurig
Een hoek op één graad nauwkeurig
Teken de bissectrice
van de hoek ß.
Teken met behulp van
een geodriehoek een
hoek van 50° op één
graad nauwkeurig.
BENODIGDHEDEN?
Om te tekenen volstaat een potlood en geodriehoek.
We gebruiken geen passer.
WAT?
Binnen wiskunde betekent construeren in tekening
brengen, met passer en liniaal.
construeer
NAUWKEURIGHEID?
Als de constructie goed is uitgevoerd zou dit moeten
leiden tot een nauwkeurige tekening.
BENODIGDHEDEN?
Je maakt gebruik van potlood, passer en liniaal. Bij
constructies wordt er zo weinig mogelijk gemeten.
(bijvoorbeeld een passeropening van 4 cm, moet wel even
gemeten worden)
definieer
WAT?
Het duidelijk omschrijven van een nieuw begrip m.b.v.
reeds gekende begrippen; dit kan zowel in woorden als in
symbolen. Je maakt gebruik van eerder gezien begrippen.
Construeer de
middelloodlijn van
lijnstijk [ AB] .
Een parallellogram is
een vierhoek met twee
paar evenwijdige zijden.
4
f)
Symbolen en afkortingen
Symbool
Lees
=
is gelijk aan
is niet gelijk aan
is bij benadering gelijk aan
<
is kleiner dan
>
is groter dan
is kleiner dan of gelijk aan
is groter dan of gelijk aan
...
is de absolute waarde van
...
1
is het omgekeerde van
hoek
staat loodrecht op
//
is evenwijdig met
//
Snijdend
~
is gelijkvormig met
p
is congruent met
A
oppervlakte
V
volume
r
straal cirkel
Ag
oppervlakte grondvlak
S
oppervlakte ruimtefiguur
omtrek
kruisend
5
2. GETALLENLEER
a) Terminologie i.v.m. bewerkingen (zie 1 a)
optelling, som, term
aftrekking, verschil
vermenigvuldiging, product, factor
deling, quotiënt, deeltal, deler, rest
machtsverheffing, macht, grondtal, exponent, kwadraat, vierkantswortel
Absolute waarde, tegengestelde en omgekeerde
Symbool
Voorbeeld
Lees
...
7 7
de absolute waarde van –7 is gelijk aan 7
...
7 7
het tegengestelde van –7 is gelijk aan 7
...
1
7 1
1
7
het omgekeerde van 7 is gelijk aan
1
7
b) Bewerkingen / Toepassen van tekenregels
Bewerking
Voorbeeld
Algemeen
2 7 2 7 9
optelling /
aftrekking
2 7 2 7 5
2 7 2 7 5
2 7 2 7 9
2 7 14
2 7 14
vermenigvuldiging
/ deling
2 7 14
2 7 14
35
7
5
35
7
5
35
7
5
35
7
5
72 7.7 49
kwadratering
vierkantsworteltrekking uitvoeren
tot de tweede macht verheffen
a² = a . a
49 7 want 72 49
Nooit de vierkantswortel trekken uit een negatief getal.
6
grondtal
exponent
uitkomst
voorbeeld
+
even
+
2² = 4
+
oneven
+
2³ = 8
-
even
+
(-3)² = 9
-
oneven
-
(-5)³= -125
machtsverheffing
uitvoeren
(
)
!!! - 3² = - 9 (er staan geen haakjes, 3 is grondtal)
Volgorde van bewerkingen
Voorbeeld
90 : 32 49 (12 10)3 .5
berekeningen tussen de haakjes moeten altijd
eerst worden uitgevoerd (haakjes wegwerken
van binnen naar buiten, eerst de ronde, dan de
90 : 32 49 23.5
vierk nte …)
de machtsverheffing en de vierkantsworteltrekking uitvoeren
de vermenigvuldiging en de deling
uitvoeren in de volgorde van links naar rechts
90 : 9 7 8.5
10 7 40
optellingen en aftrekkingen uitvoeren in de
volgorde van links naar rechts
43
Het mooie witte veulen draaft op en af.
7
Eigenschappen v. bewerkingen
Voorbeeld / Algemeen
37 7 3
3 7 7 3
commutativiteit
ab ba
a b ba
1 5 5 1 5 5 11
7 5 2 7 5 2 70
associativiteit
a b c a b c
a b c a b c
3 99 = 3 (100 - 1) = 300 - 3 = 297
distributiviteit
a b c a b a c
0 is het neutraal element voor de optelling in Q
a+0=a=0+a
neutraal element
1 is het neutraal element voor de vermenigvuldiging in Q
a.1=a=1.a
opslorpend element
0 is het opslorpend element voor de vermenigvuldiging in Q
a.0=0=0.a
Vergelijkingen van het type
x b c, a x b, ax b c
Voorbeeld
x 3 2
x 2 3
x 5
a 0
Oplossingsmethode
x+a=b
<=> x = b - a
x–a=b
<=> x = b + a
5
x 25
3
5
3
3
x 25.
5
x 15
x 25 :
ax = b
<=> x =
x:a=b
<=> x = b . a
8
5x 3 7
5x 7 3
5 x 10
ax + b = c
<=> ax = c – b
10
5
x2
x
<=> x =
c-
3. MEETKUNDE
Veel voorkomende symbolen:
ˆ
A, a, AB, AB , a b, AB , Aˆ , BAC
zie onderdeel 1.
Terminologie i.v.m. meetkundige begrippen:
vlak, punt, rechte
lijnstuk, halfrechte
lengte, afstand, hoek
Soorten hoeken
Hoek
Figuur
Omschrijving
Een rechte hoek is een hoek waarvan de
rechte hoek
gestrekte
hoek
benen loodrecht op elkaar staan. Â = 90°
Een gestrekte hoek is een hoek waarvan de
benen in elkaars verlengde liggen. Â =
180°
nulhoek
Een nulhoek is een hoek waarvan de benen
samenvallen. Â = 0°
scherpe
hoek
Een scherpe hoek is een hoek die kleiner is
dan een rechte hoek.
9
stompe
hoek
Een stompe hoek is een hoek die groter is
dan 90° en kleiner dan180°.
10
Merkwaardige lijnen
Lijnen
Figuur
Definitie
De middelloodlijn van een lijnstuk is
middelloodlijn van
een lijnstuk
een rechte die loodrecht door het
midden van het lijnstuk gaat.
De bissectrice (deellijn) van een
deellijn/bissectrice
hoek is een rechte die de hoek in
twee even grote hoeken verdeelt.
De hoogtelijn in een driehoek is een
rechte door een hoekpunt van de
hoogtelijn
driehoek die loodrecht staat op de
drager van de overstaande zijde
van dat hoekpunt.
De zwaartelijn in een driehoek is
een rechte door een hoekpunt van
de driehoek die door het midden
zwaartelijn
van de overstaande zijde van dat
hoekpunt gaat.
Schaal
Naam
breukschaal
Voorbeeld
1
de werkelijkheid is 1000 maal verkleind
1000
1: 4 de werkelijkheid is 4 maal verkleind
lijnschaal
50 km komt overeen met 5 cm
11
Soorten driehoeken
Een scherphoekige driehoek is een
driehoek met drie scherpe hoeken.
p som van de zijden
scherphoekige
driehoek
A
schuine zijde =
hypothenusa
rechthoekige
driehoek
bh
2
Een rechthoekige driehoek is een driehoek
met een rechte hoek.
rechthoekszijde
Een stomphoekige driehoek is een
driehoek met een stompe hoek.
stomphoekige
driehoek
top
gelijkbenige
driehoek
Een gelijkbenige driehoek is een driehoek
waarvan ten minste twee zijden even lang
zijn.
benen
basishoek
Een gelijkzijdige driehoek is een driehoek
waarvan de drie zijden even lang zijn.
gelijkzijdige
driehoek
De cirkel
p 2 r
cirkel
A r2
12
Soorten vierhoeken
Vierhoeken
Figuur
Definitie, Omtrek, Oppervlakte
Een trapezium is een vierhoek met
tenminste één paar evenwijdige zijden.
trapezium
p som van de zijden
A
b B h
2
Een parallellogram is een vierhoek met
twee paar evenwijdige zijden.
parallellogram
p som van de zijden
A bh
Een ruit is een vierhoek met vier even
lange zijden.
ruit
p 4.z
A
Dd
2
Een rechthoek is een vierhoek met vier
rechte hoeken.
rechthoek
p 2 l b
A l b
Een vierkant is een vierhoek met vier
rechte hoeken en vier even lange zijden.
vierkant
p 4 z
A z2
13
Kubus, balk, prisma, piramide, cilinder, kegel, bol
Ruimtefiguur
Figuur
Oppervlakte
Volume
V z3
kubus
S = 6z²
balk
S = 2.(l.b+l.h+b.h)
V = Ag.h = l.b.h
cilinder
S = 2.π.r² + 2 π.r.h
V = Ag.h = π.r².h
prisma
kegel
bol
V=
.r³.π
14