toets 3h blok D (t/m opg 25)

Schoolexamen HAVO 4 Wiskunde B
MW9 WB deel 1: Hfd. 1 t/m 4
Januari 2008
Geef bij elk antwoord een berekening of een toelichting.
Indien je gebruik maakt van de bijzondere functies van je GR schrijf dan elke stap op!
Opgave 1
Gegeven is de functie f ( x)   x3  4x2
3p.
a
Bereken exact coördinaten van de nulpunten van f(x).
3p.
b
Ga na voor welke x-waarden de grafiek van f(x) horizontaal loopt.
3p.
c
Voor de afgeleide functie geldt:
f ' ( x)  3x 2  8x .
Voor welke waarde van x is de helling van de grafiek van f(x) het grootst?
Geef je antwoord in één decimaal nauwkeurig.
Opgave 2
Los de volgende vergelijkingen en ongelijkheden exact op.
4p.
a
5(1  x)  3  2( x  3)
4p.
b
(3  2 x)(2  3x)  6 x 2  8x  1
4p.
c
3p.
d
2
 x 1
x 1
4p.
e
x  x  7  7  2x
x 2  4 x  19  2 x  2
y
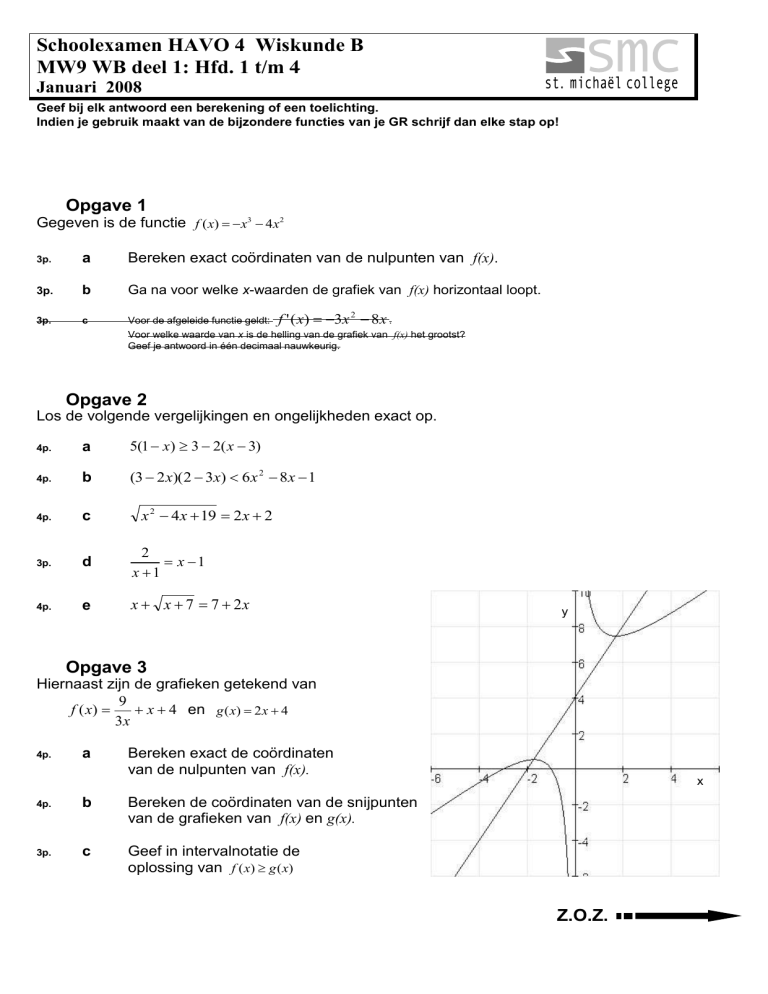
Opgave 3
Hiernaast zijn de grafieken getekend van
9
f ( x) 
 x  4 en g ( x)  2 x  4
3x
4p.
a
Bereken exact de coördinaten
van de nulpunten van f(x).
4p.
b
Bereken de coördinaten van de snijpunten
van de grafieken van f(x) en g(x).
3p.
c
Geef in intervalnotatie de
oplossing van f ( x)  g ( x)
x
Z.O.Z.
Opgave 4
Los exact op:
3p.
a
32 x1  19
3p.
b
25x3  5
3p.
c
8  24 x  32
3p.
d
1
7
 49 x  7 x
2
Opgave 5
Gegeven is de functie h( x) 
(2 x  6)
x
2p.
a
Bereken de coördinaten van het randpunt van de grafiek van h(x).
2p.
b
Geef de coördinaten van het maximum van de grafiek van h(x).
5p.
c
Plot én schets de grafiek van h(x). Geef de belangrijke punten aan.
3p.
d
Geef het domein én het bereik van h(x) in de intervalnotatie.
Opgave 6
(vervalt)
Opgave 7
2p.
a
Schrijf g ( x)  ( 19 ) x  2 in de vorm g ( x)  b  ( 19 ) x en geef de waarde van b.
3p.
b
Herschrijf de functie h( x)  3  ( 12 ) 3 x 1 in de vorm h( x)  b  g x
3p.
c
Bereken a als de functie f(x) als volgt wordt herschreven: f ( x)  81  3x  3x2a
Opgave 8
In een Wombatkolonie van 2500 Wombats (een soort zanddraak in West-Australië) breekt een
dodelijke ziekte uit. Het aantal zieke Wombats groeit exponentieel. Per 12 dagen wordt het
aantal zieke Wombats drie maal zo groot.
2p.
a
Bereken de groeifactor per dag (in 3 decimalen nauwkeurig).
3p.
b
Op het moment dat men de ziekte ontdekt (t=0) zijn er 15 Wombats ziek .
Bereken na hoeveel dagen er 1500 Wombats ziek zullen zijn.
-----