Vervalreeks - CMA

Vervalreeks
NATUURKUNDE
Radioactiviteit
Toelichting
Radioactief verval
Radioactief verval wordt met de volgende formule(s) beschreven.
1)
N (t) = N0 · e(
t)
N (t) = N0 ·
t
1 th
2
Waarin λ de vervalconstante is en th de halveringstijd. N0 is de beginhoeveelheid atomen.
De vervalconstante wordt meestal weergegeven met de eenheden s-1 of min-1. De
vervalconstante of halveringstijd zijn karakteristiek voor een bepaalde radioactieve stof.
Met de meting van deze grootheden is de radioactieve atoomsoort te bepalen. De
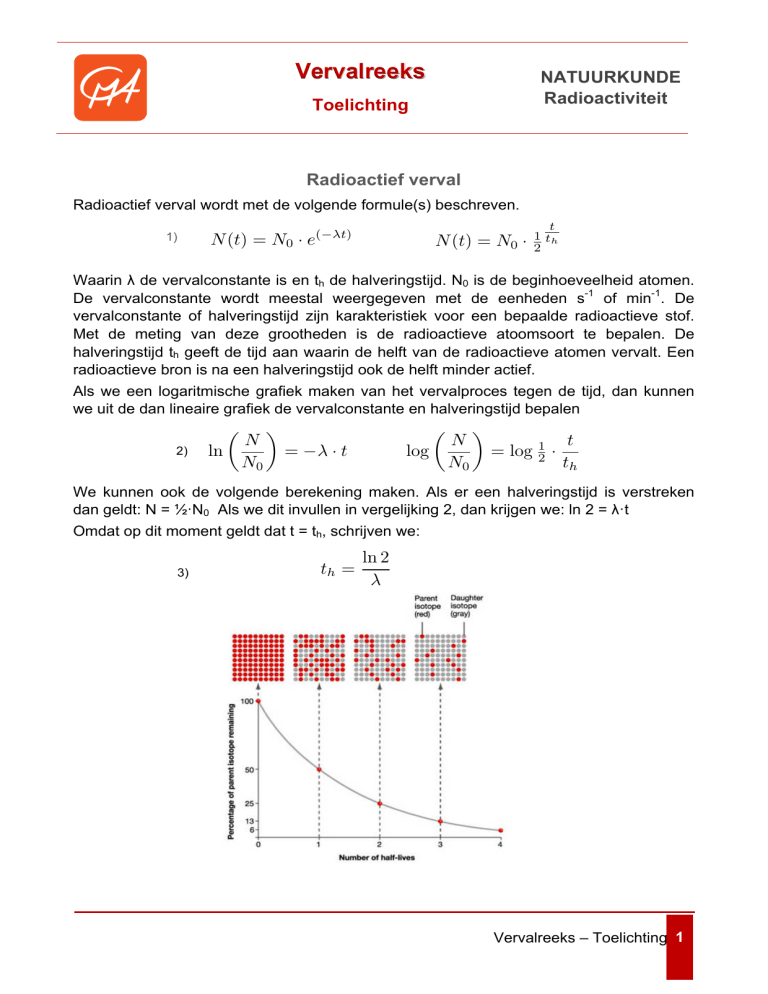
halveringstijd th geeft de tijd aan waarin de helft van de radioactieve atomen vervalt. Een
radioactieve bron is na een halveringstijd ook de helft minder actief.
Als we een logaritmische grafiek maken van het vervalproces tegen de tijd, dan kunnen
we uit de dan lineaire grafiek de vervalconstante en halveringstijd bepalen
2)
ln
✓
N
N0
◆
=
·t
log
✓
N
N0
◆
= log 12 ·
t
th
We kunnen ook de volgende berekening maken. Als er een halveringstijd is verstreken
dan geldt: N = ½·N0 Als we dit invullen in vergelijking 2, dan krijgen we: ln 2 = λ·t
Omdat op dit moment geldt dat t = th, schrijven we:
3)
th =
ln 2
Vervalreeks – Toelichting 1
De halveringstijd van radioactieve stoffen varieert. Sommige radioactieve atoomsoorten
zijn erg onstabiel en vervallen heel snel. Zij hebben een halveringstijd van minder dan een
seconde. Andere radioactieve atoomsoorten hebben halveringstijden in orde van
duizenden of zelfs miljoenen jaren. De kortlevende isotoop Ba-137m is erg geschikt om te
meten en is gemakkelijk te maken met een Cs-137/Ba-137m isotopen generator of ‘koe’.
Radioactief Verval Modelleren
Bij het radioactief verval wordt het volgende aangenomen:
•
•
•
Er is een bepaalde hoeveelheid radioactief materiaal, dat bestaat uit een aantal
kernen N.
De verandering van de hoeveelheid radioactief materiaal dN/dt wordt weergegeven
door zijn activiteit (A), deze grootheid geeft aan hoeveel kernen per tijdseenheid
vervallen.
De activiteit van een bron is gerelateerd aan de waarschijnlijkheid van het verval en
hangt af van het aantal aanwezige kernen en de waarschijnlijkheid dat de kern zal
vervallen in een bepaalde tijdseenheid (verval constant λ)
In formulevorm:
4)
A(t) =
dN (t)
=
dt
· N (t)
In de modelomgeving van Coach wordt dit gegeven vertaald naar een grafisch model.
Na het runnen van het model geeft de analytische oplossing het exponentiele verval weer
zoals dat in vergelijking 1 te zien is.
Tevens zullen we in deze modelleeractiviteit het verval van dochterkernen mee gaan
modelleren.
Voor de activiteit A geldt:
5)
2
CMA Lesmateriaal
A(t) = A0 · e(
t)
Als zowel moeder (P) en dochterkern (D) radioactief zijn, dan wordt hun activiteit gegeven
door:
AP (t) = AP,0 · e(
6)
th,P
AD (t) = AP,0
th,P th,D
t)
✓
= e(ln 2/th )
e
ln 2
th,P t
e
ln 2
th,D t
◆
waarin t1/2, de respectievelijke halveringstijden zijn van de moeder- en dochterkern.
In deze activiteit zullen we het verval van moeder en dochterkern in een grafisch model
modelleren en de effecten van de verschillende halveringstijden onderzoeken, op zowel
het verval van het aantal kernen, als op de activiteit van beide radioactieve bronnen.
In deze activiteit kijken we vooral naar het verval van Ca-47 naar Sc-47. Sc-47 vervalt zelf
ook weer naar het stabiele Ti-47. Deze reeks is gebaseerd op de opgave uit het CE
natuurkunde 6VWO van 2016, 1e tijdvak.
Vervalreeks – Toelichting 3