I KINEMATICA

Deel 1: KINEMATICA
2.1 Positie en verplaatsing
1. Een trein rijdt van Tongeren naar Hasselt, 20km verder, naar Aarschot, nog 50km verder.
Dan rijdt hij terug naar Hasselt. We beschouwen het traject als rechtlijnig.
Bereken de verplaatsing en de afgelegde weg:
 Voor de rit Tongeren-Aarschot
 Voor de rit Tongeren-Aarschot-Hasselt
2. Jan fietst naar Ben toe die 5km verder woont. Zijn plaatscoördinaat als functie van de tijd
is gegeven in de volgende figuur:
Bereken de verplaatsing en de afgelegde weg:
 Als Jan heen fietst;
 Als Jan terug fietst;
 Over het hele traject;
 Wat betekent het horizontale stuk?
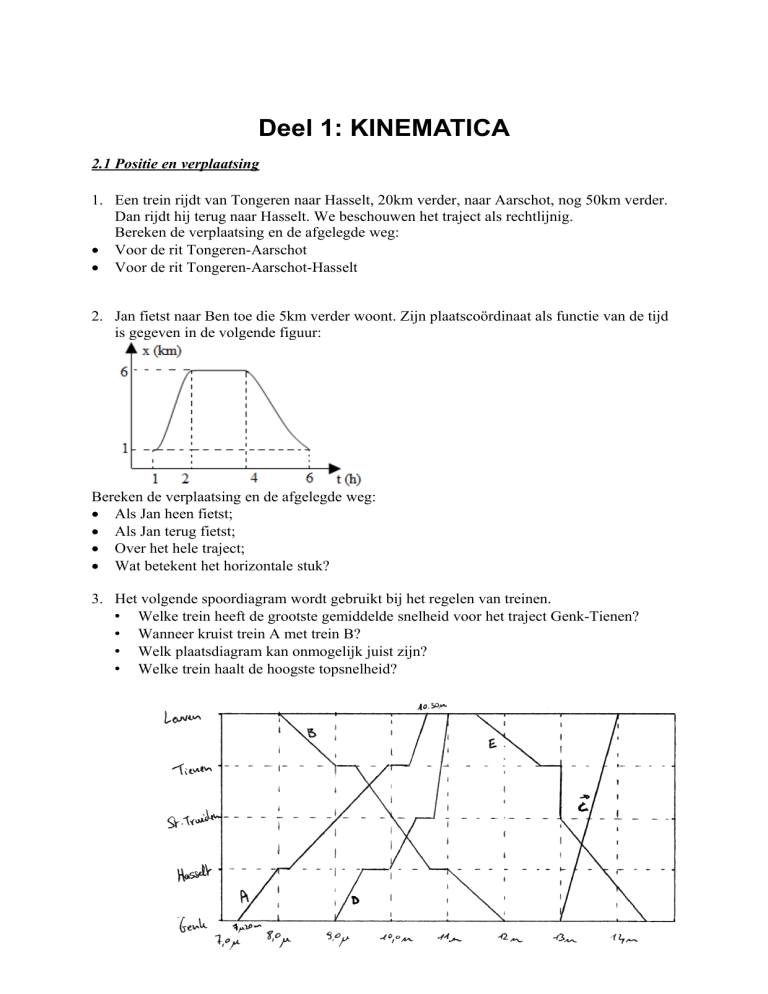
3. Het volgende spoordiagram wordt gebruikt bij het regelen van treinen.
• Welke trein heeft de grootste gemiddelde snelheid voor het traject Genk-Tienen?
• Wanneer kruist trein A met trein B?
• Welk plaatsdiagram kan onmogelijk juist zijn?
• Welke trein haalt de hoogste topsnelheid?
4.
Belle fietst van Sluizen naar Val-Meer (A→B). Zoek de afgelegde weg. De schaal van de
kaart is 1:50000
2.2.1 Gemiddelde snelheid
1.
Een auto rijdt op een rechte baan van Herentals naar Lier, een afstand van 15,0km. Hij legt
die afstand af in 720s. Bereken de gemiddelde snelheid van de auto.
2.
De snelheid van een sprinter is 10m/s. Zet deze snelheid om in km/u.
3.
Een fietser rijdt 500m met een gemiddelde snelheid van 8,5m/s. Dan rijdt hij nog 2500m in
een tijd van 7min 30s. Bereken zijn gemiddelde snelheid voor het hele traject.
4.
De grafiek geeft de beweging aan van twee treinen. Bereken de gemiddelde snelheid van elke
trein tussen:
a) t=0s en t=20s
b) t=10s en t=20s.
x (m)
400
200
100
10
20
t (s)
2.2.2 Ogenblikkelijke snelheid
1.
De plaatscoördinaat in functie van de tijd tussen 0s en 3s wordt gegeven door:
x(t )  1,5 . t 2  2.t
Bereken v(t=3,0s).
2.
De plaatscoördinaat van een fietser als functie van de tijd wordt voor tijden tussen 0 s en 3s
gegeven door: x(t )  1.t 2  0,5.t  0,25
a. Teken de x(t)- en v(t)-grafiek voor tijden tussen 0 s en 3 s.
b. Bereken zijn snelheid op t=1,0s.
c. Bereken zijn snelheid op het ogenblik t=2,0s.
d. Wat is de gemiddelde snelheid van 0 s tot 2,0s?
3.
Een voorwerp voert een beweging uit op een rechte lijn volgens de volgende
bewegingsvergelijking:
x (t )  3. t 2  4. t  2
a. Maak een x(t)-grafiek en een v(t)-grafiek van t = 0s tot t = 2s (om de 0,25s)
b. Bereken de gemiddelde snelheid gedurende de eerste seconde van de beweging en de
laatste seconde.
x (m)
4.
De positie van een wagen, werd gemeten op
verschillende tijdstippen. De resultaten vind je
in de figuur. Zoek de snelheid op t = 2,0s.
14
12
10
8
6
4
2
0
0
1
2
3
4
t (s)
5
6
7
8
2.5 De eenparige beweging
1.
Een fietser vertrekt op een bepaald ogenblik om een afstand van 100km af te leggen en rijdt
tegen een constante snelheid van 20,0 km/h. Een tweede fietser vertrekt 30,0min later en rijdt
tegen een constante snelheid van 25,0 km/h.
 Wanneer komt de eerste fietser aan?
 En wanneer de tweede?
 Waar en wanneer haalt de tweede fietser de eerste in?
 Controleer de juistheid van je antwoord met een x(t)-diagram.
2.
Een auto vertrekt uit een plaats A met een constante snelheid van 60,0 km/h. Op hetzelfde
ogenblik vertrekt er ook uit A een andere wagen met een constante snelheid van 30,0 km/h.
Na 1,00 h valt de tweede wagen stil en kan slechts twee uur later verder rijden, dit keer met
een snelheid van 90,0 km/h.
 Construeer voor beide wagens het plaatsdiagram.
 Waar en wanneer komen ze samen?
3.
De afstand Tongeren - Antwerpen is 138 km. Tezelfdertijd vertrekken twee treinen: een uit
Tongeren naar Antwerpen met een constante snelheid van 100 km/h en een vanuit Antwerpen
naar Tongeren met een constante snelheid van 90,0 km/h. Waar en wanneer kruisen beide
treinen elkaar? Controleer aan de hand van een x(t)-diagram. (t-as van 0 tot 1h uitzetten)
4.
Fons en Jaak bevinden zich op 1,00 km van elkaar en komen naar elkaar toe. Jaak vertrekt
100 s na Fons en beweegt dubbel zo vlug. De ontmoeting gebeurt 400 m van het vertrekpunt
van Fons. Bereken de snelheden en stel de beweging grafisch voor.
5.
Tessy en Philip voeren op een rechte en vanuit hetzelfde beginpunt een eenparige beweging
uit. Tessy vertrekt 100s voor Philip. Met een snelheid die het dubbel is van de snelheid van
Tessy haalt Philip Tessy in op 400 m van het vertrekpunt. Bereken beide snelheden en stel ze
grafisch voor.
6.
Frens en Let bevinden zich op 2000 m van elkaar en komen naar elkaar toe. Frens wandelt
aan een snelheid van 0,50 m/s en Let verplaatst zich met 1,30 m in 1,0 s en vertrekt 800 s
later.
a) Waar en wanneer kruisen ze elkaar?
b) Controleer je antwoordt met een x(t)-grafiek.
7.
Raf en Ronny bevinden zich op 100m van elkaar en komen naar elkaar toe. Ronny loopt
1,5keer sneller als Raf maar vertrekt 10s later. Ze kruisen op 64m van het beginpunt van Raf.
Bereken hun snelheden. Maak een x(t)-grafiek.
8.
Bij een wielerwedstrijd staat een reporter op 528m van de finish. Op een zeker ogenblik fietst
Pantani voorbij. De reporter drukt dan zijn chronometer in. 5,0s later rijdt Armstrong langs.
Aan de finish heeft Armstrong 38m voorsprong op Pantani. Armstrong fietste 1,2 keer sneller
als Pantani.
Bereken hun snelheden.
9.
Twee ridders staan aan weerszijde van een 100m lange rechte baan. Een zwarte ridder vertrekt
2s later als de witte. De snelheid van zwart is dubbel zo groot als die van wit. Als de witte
ridder 40m heeft afgelegd, raakt hij de zwarte met zijn lans. (lengte van de lans=5m).
Bereken hun snelheden. Maak een x(t)-grafiek.
2.3.1 De gemiddelde versnelling
1.
Een bus rijdt met een snelheid van 3,0m/s. Na 15 s is de snelheid 20m/s. Wat is de
gemiddelde versnelling?
2.
Beoordeel de volgende uitspraak:
“Als de versnelling negatief is, is de beweging vertraagd.”
3.
Een raket heeft op een bepaald ogenblik een snelheid van 110m/s; 50,0s later is die snelheid
gelijk aan 220m/s. Gedurende de volgende 10,0s neemt de snelheid toe; de versnelling is dan
2,85m/s².
Bereken:
a. de gemiddelde versnelling van de raket in de eerste 50,0s.
b. de snelheid van de raket 60,0s later
c. de gemiddelde versnelling over het hele traject.
2.3.2 De ogenblikkelijke versnelling
1.
Een auto op afstandsbesturing heeft als plaatscoördinaat:
x(t )  1,0m  3,0m / s ².t ²
Bereken:
a. de snelheid op t=0,0s en t=3,0s
b. de gemiddelde versnelling in het tijdsinterval t=0s tot t=3,0s
c. de versnelling op t=3,0s
2.
Gegeven: x(t )  t 3  9.t
- Op welk ogenblik is de snelheid nul?
- Waar bevindt de massa zich op dat ogenblik?
- Hoe groot is de versnelling op dat ogenblik?
- Wanneer is het voorwerp in de oorsprong?
3.
Bart beweegt volgens de plaatscoördinaat:
x(t )  2.t 2  10.t  10
Joke beweegt volgens de plaatsfunctie:
x(t )  t 2  2.t  2
- Op welke tijdstippen ontmoeten ze elkaar?
- Hoe groot zijn hun snelheden op die ogenblikken?
- Op welk ogenblik kruisen ze elkaar? Wanneer halen ze elkaar in?
4.
Een puntmassa beweegt volgens de plaatsfunctie:
x(t )  t 2  6.t  7
- Op welk ogenblik is de snelheid nul?
- Hoe groot is dan de versnelling?
- Op welk ogenblik is de massa in het vertrekpunt terug?
- Op welk ogenblik is de massa in de oorsprong?
5.
De versnelling van een vliegtuig bij de start neemt gelijkmatig toe:
a(t )  6.t  1
Het vliegtuig start vanuit de oorsprong met een snelheid van 2m/s.
Zoek zijn snelheids- en positievergelijking.
Wanneer is zijn snelheid gelijk aan 20m/s?
Wat is zijn plaatscoördinaat dan?
2.4 De eenparig veranderlijke beweging
1.
Een skiër daalt vanuit rust op t=0s een berghelling af met een constante versnelling van
4,0m/s².
Bereken:
a) de plaatscoördinaat na 3,0s.
b) de snelheid na 3,0s.
2.
Een auto rijdt aan 28m/s en remt met een constante versnelling van 4,0m/s².
a) Op welk ogenblik komt hij tot stilstand?
b) Wat is de plaatscoördinaat van de auto na het remmen?
3.
Jan rijdt vanuit stilstand met zijn fiets een helling van 240m af met een constante versnelling
van 0,60m/s².
Bereken:
a) de verplaatsing na 2,0s,
b) op welk ogenblik hij beneden aankomt,
c) de snelheid waarmee hij beneden aankomt.
4.
Twee fietsers vertrekken gelijktijdig om een afstand van 200 m af te leggen. De eerste rijdt
met een constante snelheid van 4,0 m/s, terwijl de tweede vertrekt met een snelheid van
1,00m/s en de afstand van 200 m met een EVRB met een versnelling van 0,20 m/s² aflegt.
Waar zal de tweede fietser de eerste inhalen en wanneer?
5.
Het snelheidsdiagram van een auto die van een horizontaal vlak naar een helling overgaat, is
rechts voorgesteld. De snelheid staat in m/s.
Bepaal:
 de soort beweging;
 de versnelling;
 wanneer de snelheid nul is;
 de verplaatsing gedurende de
eerste 30 s;
 de gemiddelde snelheid
gedurende deze 30 s.
v (m /s )
70
60
50
40
30
20
10
0
0
5
10
15
20
25
30
t (s )
6.
Het snelheidsdiagram van een racewagen is op de figuur voorgesteld.
 Beschrijf de beweging (soort beweging en
versnelling);
 bereken de verplaatsing tussen de tweede
en de achtste seconde;
 bereken de gemiddelde snelheid tussen de
tweede en de achtste seconde.
v (m /s)
48
36
24
12
0
0
1
2
3
4
5
6
7
8
t (s)
7.
Bij een wagen, die eerst een helling af -, en vervolgens een helling oprijdt, ziet het
snelheidsdiagram er zoals op de figuur uit:
v (m /s )
120
 Beschrijf de beweging (soort beweging en
versnelling);
 bereken de positie na 20 s;
 bereken de gemiddelde snelheid gedurende
deze 20 s.
80
40
0
0
5
10
15
20
t (s)
8.
Een voorwerp, dat eenparig veranderlijk rechtlijnig beweegt, bevindt zich op t = 0 s in een
punt 30 m links van de oorsprong. Het heeft een beginsnelheid van 20 m/s naar rechts en een
versnelling van 4,0 m/s² naar links. Wanneer is zijn snelheid 0 m/s, Waar bevindt het zich
dan? Wanneer is de beweging vertraagd, en wanneer is ze versneld?
9.
Een bal wordt omhoog geschoten met een snelheid van 20m/s. Hoelang zal het duren
vooraleer deze bal het hoogste punt bereikt heeft?
10.
Een auto A rijdt aan een constante snelheid v over een rechte weg. Een tweede auto B zit s
meter achter A, heeft een snelheid v’ en remt met een versnelling |a’|. Bewijs dat ze tegen
elkaar zullen botsen als:
 2. a' .s  (v'v)²  0
11.
Van op een 300m hoge mast valt een steen vrij naar beneden. Op hetzelfde ogenblik dat de
steen vertrekt, werp iemand een tweede steen verticaal de lucht in met een beginsnelheid van
60m/s.
Op welke hoogte passeren de stenen elkaar?
12.
Je laat een steen vanuit rust in een waterput vallen. Na 1,50s neem je een plonzend geluid
waar. Zoek de diepte van de put indien je weet dat de geluidssnelheid constant is en gelijk aan
300m/s. We nemen aan dat er geen wrijvingskrachten zijn.
13.
Een voorwerp voert een EVRB uit. De positie op enkele ogenblikken kan afgelezen worden in
de volgende x(t)-grafiek:
Zoek de snelheid op t=4,0s.
160
140
120
x (m)
100
80
60
40
20
0
0
1
2
3
t (s)
4
5
3.1-3.3 Positievector, snelheidvector, versnellingsvector
1.
Een papieren vliegtuigje wordt uit het raam geworpen. Het verwijdert zich met een constante
snelheid van 0,8m/s van de muur. Door de wind wijkt het van haar rechtlijnige baan af
volgens de formule:
d  0,4.t ²
a) Schets de baan die het vliegtuig aflegt in de eerste vier seconden
b) Teken en bereken de verplaatsing voor deze periode
c) Teken en bereken de gemiddelde snelheid voor deze periode
d) Teken en bereken de snelheid op t=2,0s
e) Teken de versnelling op t=2,0s
2.
Je bekijkt van bovenuit de beweging van een mier. De baan is geschetst in de volgende figuur.
Construeer en bereken (indien mogelijk):
x ( t )   t ²  5.t
2.
y( t )  4. sin(
.t )
4
5
4
3
2
1
0
0
2
4
6
8
10
-1
-2
-3
-4
-5
a) de verplaatsing en de gemiddelde snelheid in het tijdsinterval van t=0s tot t=4,0s
b) de ogenblikkelijk snelheid op t=2,0s en t=3,0s
c) de gemiddelde versnelling in het tijdsinterval van t=2,0s tot t=3,0s
3.5. De schuine worp
1.
Een pijl wordt afgeschoten onder een hoek van 30° met een snelheid van 15m/s.
a) Maak een schets van de baan.
b) Bereken de maximale hoogte.
c) Hoe groot is de snelheid op een halve meter hoogte?
2.
Een kogelstoter stoot een kogel weg onder een hoek van 30° met een beginsnelheid van
8,0m/s. De bal is dan 2,20m boven de grond.
Bereken:
a) de plaatsvector na 0,50s
b) de snelheidsvector na 0,50s
c) de horizontale plaatscoördinaat van de kogel als die op de grond valt.
3.
Een kogel wordt in horizontale richting met een snelheid van 800m/s afgeschoten op een
schietschijf die zich op 100m afstand van de schutter bevindt. Als hij precies op de roos mikt,
over welke afstand is de kogel afgezakt als hij de schijf treft?
4.
Een tennisspeler, die 9,0m voor het net staat, slaat de bal in horizontale richting met een
snelheid van 25m/s. Het racket raakt de bal 1,8m boven de grond. De bovenkant van het net is
1,00m boven de grond. Vliegt de bal over het net, of er tegenaan?
5.
Een auto rijdt door een brugleuning en komt 5,2m lager in het water terecht. De horizontale
afstand tussen de plaats waar hij door de leuning ging en waar hij in het water terecht kwam,
is 22m. Met welke snelheid reed de bestuurder door de leuning?
6.
Een projectiel wordt met een beginsnelheid van 350m/s onder een hoek van 30° met de
horizontale afgeschoten.
- Welke hoogte bereikt het projectiel?
- Bereken de dracht.
7.
Verschillende tennisballen worden weggeschoten met een even grote snelheid maar onder een
verschillende hoek. De tennisbal die de grootste dracht bereikt, wordt afgeschoten onder een
hoek van: …..°.
8.
Van op de top van een kerktoren van 75,0m hoog schiet men een projectiel onder een hoek
van 40° met de horizontale weg. De grootte van de beginsnelheid is 400m/s. Na hoeveel tijd
bereikt het projectiel de grond, en op welke afstand van de toren?
9.
Els skiet een schans af. Op het einde van de schans is haar snelheid 9,0m/s en volledig
horizontaal. De helling daaronder ligt 2,0m onder de schans en daalt aan een hoek van 30°.
Zoek het bereik van haar sprong.
2,0m
30°
3.7 De cirkelbeweging
1.
Een atleet slingert een hamer in een horizontaal vlak rond. De ketting is 1,2m lang, de hamer
draait in 2,0s vijfmaal rond.
Zoek:
a) de periode
b) de frequentie
c) de grootte van de hoeksnelheid
d) de grootte van de snelheid
e) de grootte van de versnelling
2.
Een wagen kan een versnelling ondergaan van 0,91.g zonder te slippen. Wat is de straal van
de kleinste cirkel die de auto met een snelheid van 45m/s kan beschrijven.
3.
Het achterwiel van Frank VdB heeft een straal van 42cm en maakt 272 omwentelingen per
minuut.
Zoek:
a) de frequentie achterwiel
b) de periode
c) de snelheid van zijn fiets
d) Vergelijk de periode van het wiel met deze van zijn pedalen (groter?, kleiner?, gelijk?) en
verklaar waarom.
4.
Een steen wordt aan een touw rondgeslingerd.
a) Welke vector stelt de snelheid voor?
b) Welke vector stelt de versnelling voor?
5.
De figuur hiernaast toont het bovenaanzicht van de baan die
gevolgd wordt door een auto. Ze bestaat uit rechte en
cirkelvormige stukken.
Van 1 tot in 5 is v constant. Tussen 5 en 6 komt de auto tot
stilstand.
a) Duid in het midden van elk stuk de snelheidsvector aan.
b) Is er in die punten een versnelling? Duid ook die aan.
c) Vergelijk de grootte van de versnelling tussen 2 en 3 met
die tussen 4 en 5.
Deel 2: DYNAMICA
1 De wetten van Newton
1.1 De eerste wet
1.
Waarom slaat de koffie over de rand, als we met de kop een plotse beweging maken?
2.
Waarom vliegen we over de stuurstang, als we plots met onze fiets remmen? Wat is er in zo'n
geval gevaarlijker: remmen op het voorwiel of remmen op het achterwiel?
3.
Verklaar waarom een caravan nooit met een kabel met de auto mag verbonden worden.
4.
Moet een fietser, die op een horizontale weg eenparig rechtlijnig fietst, toch blijven trappen?
Verklaar.
5.
Waarom is het te verwachten, dat de topsnelheid bij een hovercraft veel hoger ligt dan bij een
schip, als beide hetzelfde vermogen ontwikkelen?
6.
Waarom is een met boomstammen geladen vrachtwagen voor de bestuurder zo gevaarlijk, als
hij bruusk moet remmen, of bij een botsing betrokken raakt?
7.
Als je van een rijdende tram wilt springen, moet je een stuk in de rijrichting meelopen. Leg
uit.
8.
Je stapelt een tiental identieke ronde schijven netjes op elkaar. Met een lat, die iets dunner is
dan de dikte van een schijf geef je een korte fikse tik tegen de onderste schijf. De schijf vliegt
onder de stapel uit en de stapel kipt niet om. Verklaar.
9.
De aarde beweegt rond de zon volgens een haan die benaderend cirkelvormig is. Hoe kan dat?
10.
Een schuin omhooggeworpen lichaam beschrijft geen rechtlijnige baan, en zijn snelheid
verandert zowel in grootte als in richting. Waarom?
11.
Is het je ooit opgevallen dat een auto heel moeilijk of helemaal niet kan vertrekken op een
spiegelglad wegdek of in de modder? Verklaar!
1.2&1.3 De tweede en derde wet
1.
Als twee krachten F⃗ 1 en F⃗ 2 in grootte onveranderd blijven, maar een veranderlijke
hoek kunnen insluiten, wat is dan de minimale en de maximale waarde van de grootte van hun
resultante. Bij welke ingesloten hoek is dit zo?
2.
Bepaal de resultante van twee krachten die op eenzelfde lichaam in hetzelfde punt inwerken
en waarvan de dragers loodrecht op elkaar staan. Hun respectieve grootten zijn 17,0 N en
24,0 N.
3.
Op een tafel staat een fles wijn. Teken en benoem de krachten die daarbij op de fles wijn
aangrijpen. Door welke lichamen worden deze krachten uitgeoefend?
4.
Een fietser met een massa van 60,2 kg rijdt op een rechte baan met een constante snelheid die
25,0 km/h bedraagt. Hoe groot is de inwerkende resulterende kracht?
5.
Beoordeel volgende uitspraak: ‘Op een voorwerp in rust kunnen er geen uitwendige krachten
werkzaam zijn.’
6.
Is het zinvol te zeggen dat een voorwerp 'kracht bezit' ? Bespreek.
7.
Boer Bavo en zijn zoon willen hun ezel verplaatsen. Deze is echter koppig en is niet vooruit te
krijgen. Van bovenaf bekeken hebben we de situatie zoals op de figuur weergegeven. Hoe
groot is de resultante van de krachten die beide mannen samen op de ezel uitoefenen?
8.
Een zak cement met massa m hangt aan drie touwen zoals weergegeven op de figuur. Het
geheel is in rust.
-
-
Bewijs dat de grootte van de spankracht
in het linkertouw te berekenen is uit:
m.g . cos( 2 )
F1 
sin( 1   2 )
Als de massa van de cement 20,4 kg
bedraagt,  1 = 10,0° en  2 = 25,0° hoe
groot zijn dan de spankrachten in de
drie touwen?
θ1
θ2
CEMENT
9
Als eenzelfde kracht inwerkt op twee verschillende massa's, dan geldt dat:
a de verkregen versnellingen gelijk zijn;
b de grootste massa de grootste versnelling heeft;
c de grootste massa de kleinste versnelling heeft;
d er over de versnellingen geen uitspraak kan gedaan worden.
10
Bereken de spannings- en drukkrachten,
die de aangeduide kracht op staaf ab en
kabel ac uitoefent.
c
a
30°
1500N
b
11
Een bol met massa m is aan een touw vastgemaakt.
Hij wordt in een verticaal vlak aan het slingeren
gebracht. De figuur stelt een momentopname voor.
Teken en benoem de krachten die op de bol aangrijpen.
Door welke lichamen worden ze uitgeoefend?
12
Een lichaam met een massa van 200 kg vertrekt uit rust en bereikt onder invloed van een
constante kracht na 50s een snelheid van 90 km/h. Bereken de grootte van de inwerkende
kracht.
13
Op een lichaam met een massa van 5,00 kg werkt gedurende 5,0 s een kracht van 10,0 N in.
Bereken de snelheid die het lichaam hierdoor krijgt.
14
Een fietser met een massa van 60,0kg rijdt op een fiets van 15,0kg. Rij vertrekt met een
beginsnelheid van 2,00 m/s en bereikt na 5,0 s zijn maximale snelheid van 36,0 km/h.
Bereken de grootte van de kracht nodig om die snelheid te bereiken.
15
Welke constante kracht moeten de remmen op de wielen van een auto met een massa van
1200 kg uitoefenen als de wagen met een snelheid van 90,0km/h rijdt en over een afstand van
60,0 m stopt?
16
Een zwaluw met een massa van 50,0 g vliegt tegen een snelheid van 54,0 km/h. Op een
afstand van 1,50 m van zijn nest begint de zwaluw te remmen en komt op zijn nest tot
stilstand. Bereken de grootte van de uitgeoefende remkracht.
17.
Een trein van 300 ton, die met een snelheid van 90 km/h rijdt, kan in 40 s tot stilstand
gebracht worden. Bereken de grootte van de remmende kracht en de remafstand.
18.
Een elektron en een proton vertrekken vanuit rust in een homogeen elektrisch veld. De
elektrische veldsterkte bedraagt 520 N/C. Hoe groot is de snelheid van elk deeltje na
48.10-9 s? Welke afstand heeft elk deeltje in deze tijd afgelegd?
Gegevens:
me = 9,1095.10-31 kg
mp = 1,6726. 10-27 kg
e = 1,6022.l0-19C
19.
Zowel bij de studie van de horizontale als van de schuine worp werd gezegd dat de beweging
een samenstelling was van een ERB met een EVRB. Maak gebruik van het tweede beginsel
van Newton om dit aan te tonen. Er werd geen rekening gehouden met de invloed van de
lucht.
20.
Drie blokken zijn op een horizontaal wrijvingsloos oppervlak met elkaar verbonden met
massaloze touwen en twee dynamometers A en B zoals op de figuur aangeduid. De massa van
deze dynamometers is eveneens te verwaarlozen.

Op het ste1sel werkt er een kracht F met een grootte van 60 N. Als m1 = 10 kg, m2 = 20 kg
en m3 = 30 kg, hoe groot is dan de kracht die de dynamometer B tussen de blokken 2 en 3
aangeeft?
21.
Twee personen staan op rolschaatsen en zijn door een touw verbonden. Wat gebeurt er, en
verklaar:
- als de ene persoon het touw inhaalt?
- als de andere persoon het touw inhaalt?
- als ze allebei gelijktijdig het touw inhalen?
22.
Je springt vanuit een roeibootje naar de oever. Verklaar wat er kan gebeuren als het roeibootje
niet of wel vastgemeerd is.
Wanneer je nu vanaf een groot binnenschip naar de oever springt, wat zou het resultaat dan
zijn? Verklaar!
23.
Wat word je gewaar als je met een wapen een kogel afvuurt? Waarom druk je best de kolf
stevig tegen de schouder aan?
24.
Waarom staat het affuit van een kanon steeds op wielen of rails?
25.
Waarom gebruikt men bij een sprint startblokken, terwijl dat bijvoorbeeld voor een
5000 m- of 10 000 m- loopwedstrijd niet hoeft?
26.
Een grote magneet oefent op een ijzeren spijkertje een kracht uit. Welke van volgende
uitspraken is dan juist ?
a) Het spijkertje zelf oefent op de magneet geen kracht uit.
b) De kracht die het spijkertje op de magneet uitoefent is veel kleiner dan deze door
de magneet op het spijkertje uitgeoefend.
c) De kracht die het spijkertje op de magneet uitoefent is even groot als deze door de
magneet op het spijkertje uitgeoefend.
d) Over de grootte van de kracht die het spijkertje op de magneet uitoefent kan niets
met zekerheid gezegd worden.
27.
Superman en Schanulleke trekken elk aan een verschillend uiteinde van hetzelfde touw.
Oefent Superman dan de grootste kracht uit op het touw of is het Schanulleke? Of oefenen
beiden een even grote kracht uit op het touw'?
1.4 Kracht bij enkele soorten beweging
1.
Welk lichaam is verantwoordelijk voor de middelpuntzoekende kracht in de onderstaande
gevallen?
 de modder op de buitenomtrek van een draaiend fietswiel;
 een trein die een bocht neemt;
 een auto in een bocht bij een horizontaal wegdek;
 het ronddraaien in een horizontaal vlak van een steen aan een touw;
 een wagentje dat een looping maakt in een achtbaan;
 een persoon in een ronddraaiende ton.
2.
Hoe groot moet de snelheid van ‘Diavolo’ zijn om bovenaan de looping het contact met de
baan niet te verliezen? De looping heeft een straal van 2,7m.
3.
Een stuntman rijdt met zijn auto over de top van een heuvel. Deze is boven bolvormig met
een straal van 250m. Wat is de grootste snelheid die hij mag hebben om het contact met de
weg niet te verliezen?
4.
Een vliegtuig vliegt in een horizontaal vlak en voert een cirkelbeweging uit met een snelheid
van 480km/h. De vleugels maken een hoek van 40° met de horizontaal. Zoek de straal van de
cirkelbeweging.
Neem aan dat de nodige kracht gegeven wordt door de ‘aerodynamische lift’ die loodrecht
staat op de vleugels.
5.
Een elektron met een snelheid van 2,0.107m/s komt in een magnetisch veld terecht. De
magnetische inductie staat loodrecht op de snelheid en heeft een grootte van 4,5.10-2T. Zoek
de straal van de cirkelbeweging. (me=9,1095.10-31kg)
6.
Tijdens het trainen van Frank De Winne wordt deze in een cirkelvormige baan gebracht met
een zetel, die zich aan het uiteinde van een horizontale arm van 5,00m lengte bevindt. Indien
de versnelling tot 10.g mag oplopen, wat is dan de toegelaten maximale snelheid?
7.
Gegeven is de volgende opstelling:
m1 voert een eenparige cirkelbeweging uit in een horizontaal vlak.
  11,5
m1  10 g
  0,30m
Zoek haar snelheid. Hoe groot is de tweede massa in dit geval?
2 De gravitatiekracht
2.2 De gravitatiekracht
1.
Bepaal de grootte van de gravitatiekracht die de planeet Mars uitoefent op een marslander die
juist geland is. De massa van de marslander is 4,0 ton.
2.
In de volgende figuur zij drie homogene bollen weergegeven. Bepaal de gravitatiekracht die
werkt op m.
3.
Waarom heeft de gravitatiekracht maar een merkbare uitwerking indien minstens één van
beide massa’s zeer groot is?
4.
Twee puntmassa’s oefenen op elkaar een gravitatiekracht uit met als grootte F . Hoe groot is
de kracht als de afstand verdubbelt?
5.
Twee sterren met respectievelijke massa’s m en 4.m bevinden zich op een afstand d van
elkaar. Waar op de verbindingslijn tussen deze sterren zou er op een derde massa geen
resulterende kracht inwerken?
2.3 Gravitatie en zwaartekracht
1.
Bereken de gravitatieversnelling op de planeet Venus.
2.
Bereken de gravitatieversnelling op 400km hoogte van de aarde. Wat is de gravitatiekracht
van de aarde op een satelliet van 2,5ton die zich op die hoogte bevindt?
3.
Een satelliet draait in een cirkelbaan rond de aarde op een hoogte van 300 km. De straal van
de aarde is 6378 km en haar massa 5,98.1024kg.
Bereken:
a de periode van de satelliet,
b de snelheid van de satelliet.
4.
Wat zijn geostationaire satellieten? Op welke hoogte draaien ze rond de aarde?
5.
In zijn ruimtepak leest Neil Armstrong op een weegschaal op aarde 245kg af.
a) Hoe groot is het gewicht op aarde?
b) Hoe groot is die massa op de maan?
c) Hoe groot is het gewicht op de maan?
d) Welke waarde leest hij op een weegschaal af op de maan?
6.
Lien staat in een lift en draagt een zak levensmiddelen met massa 12,6kg.
a) Waar grijpt het gewicht van de zak aan?
b) Bereken het gewicht van de zak
• als de lift in rust is;
• als ze opwaarts vertrekt met een versnelling van 3,0m/s².
7.
De spaceshuttle draait rondjes rond de aarde. Waarom zijn de astronauten gewichtloos?
3 Wrijvings- en weerstandskrachten
1.
Een massa van 50,0g wordt door een horizontale kracht van 0,065N voortbewogen. Het legt
onder de werking van deze kracht en de wrijvingskracht vanuit de rusttoestand in 10,0s op een
rechte baan een afstand af van 40,7m. Hoe groot is de wrijvingskracht en de wrijvingsfactor?
2.
Op de luchthaven trekt een vrouw door middel van een riem haar koffer met een constante
snelheid verder. De riem maakt een hoek  met de horizontale. De massa van het koffer is
20,5kg. De vrouw trekt aan de riem met een kracht van 35,6N terwijl de grootte van de
wrijvingskracht op de valies 20,3N bedraagt.
• Teken de krachten die op het koffer aangrijpen.
• Hoe groot is de hoek tussen de riem en de horizontale?
• Hoe groot is de normaalkracht?
• Bepaal de wrijvingsfactor.
3.
Een hockeyschijfje of puck op een bevroren vijver krijgt een horizontale slag waardoor het
met een snelheid van 20,5m/s vertrekt. Na 120m komt de puck tot rust.
a) Teken en benoem de krachten die op de puck aangrijpen nadat het de slag heeft gekregen.
b) Hoe groot is de wrijvingsfactor?
4.
Bepaal de remafstand van een auto in functie van haar snelheid. De wrijvingsfactor (rubberbeton) is 0,80.
5.
Een motorfietser neemt een scherpe bocht met een straal van 30m tegen een snelheid van
72km/h. Het wegdek in de bocht is horizontaal. Hij helt naar de binnenzijde van de bocht. De
totale massa van de man en motorfiets bedraagt 100kg.
Zal hij in de bocht blijven als gegeven is dat de grootte van de maximale wrijvingskracht van
de weg op de banden gelijk is aan de grootte van de zwaartekracht? Hoe groot is de
wrijvingsfactor?
6.
Waarom is het noodzakelijk dat een aardsatelliet buiten de dampkring rond de aarde moet
draaien?
7.
Twee bollen met dezelfde straal worden vanop een hoog gebouw losgelaten. De ene is van
hout, de andere van ijzer. Welke bol ondervindt dan tijdens zijn val de grootste
weerstandskracht vanwege de lucht? Of is de weerstandskracht op beide bollen even groot?
8.
In Nevada en Zuid-Californië laten stenen sporen achter in het harde droge zand. Het lijkt
alsof de stenen vanzelf over de bodem rollen.
Jarenlang zocht men naar een verklaring hiervoor. Het antwoord kwam in 1970, toen er
toevallig een storm woedde over de woestijn. De bovenlaag veranderde in een dunne laag
modder, dat de wrijvingscoëfficiënt tussen steen en bodem fel deed dalen. Als dit bovendien
gepaard gaat met een stevige wind, kunnen de stenen door deze duwkracht beginnen te rollen
zodat ze een spoor achterlaten dat later hard gebakken wordt door de zon.
Veronderstel dat een steen een massa heeft van 300kg en dat de wrijvingscoëfficiënt verkleind
is tot 0,15. Hoe groot moet de kracht zijn om de steen in beweging te brengen?
Hoe snel waait de wind als de steen bolvormig is en een diameter heeft van 0,40m?
9.
Onmiddellijk na zijn sprong uit het vliegtuig valt Eddy gedurende een zekere tijd door de
lucht met toenemende snelheid. Tijdens deze valbeweging zal de grootte van de versnelling:
• toenemen
• afnemen;
• constant blijven
• eerst afnemen en dan toenemen.
10
Zoek de topsnelheid van een bal van 0,50kg (r = 0,15m) als ge deze vanop grote hoogte laat
vallen. ( C x  0,50 en   1,2kg / m ³ )
11.
Maak een grafiek voor een standaardfiets waarbij je de snelheid uitzet in functie van het
vermogen. Doe hetzelfde voor de racefiets.
12.
Zoek de topsnelheid van een Mini Austin als we mogen aannemen dat het vermogen van 5 pk
volledig gebruikt wordt om de weerstandskracht te overwinnen.( 1 pk = 7,355.10²W )
Cx waarden
Cx
0,30
0,31
0,35
0,35
0,39
Audi 100
Porsche 924
Opel Corsa SR
Renault 5
Mini Austin
M5 Lowracer met sandwichkuip
M5 Lowracer met staartpunt
M5 Lowracer
Racefiets
Standaardfiets
Bol
0,50
A (m²)
2,05
1,79
1,73
1,75
1,73
Cx.A (m²)
0,62
0,56
0,61
0,62
0,67
0,123
0,193
0,244
0,593
0,70 – 0,80
Deel 3: ARBEID EN ENERGIE
1. Arbeid
1.
Bereken de arbeid in volgende gevallen. De kracht is steeds gelijk aan 20N, de verplaatsing
40m.:
F
F
F
2
Een ruimtetuig heeft zich van de aantrekkingskracht van alle sterren en planeten
losgemaakt en beweegt eenparig rechtlijnig in de ruimte. Geen enkele motor, noch de raket
is ingeschakeld. Wat kun je hier vertellen over de arbeid door of op het ruimtetuig
geleverd?
3
Toontje verplaatst een zware kist van 100 kg 3,2 m horizontaal over de vloer. Welke arbeid
levert de zwaartekracht tijdens deze verplaatsing?
4
Een steen, aan het uiteinde van een touw vastgemaakt, wordt in een horizontaal vlak
rondgeslingerd. De snelheid waarmee de cirkel doorlopen wordt, blijft steeds even groot.
Hoe groot is de arbeid die de spankracht van het touw op de steen levert?
5
Een arbeider met een massa van 75,0 kg draagt een zak van 50,0 kg twee verdiepingen van
elk 3,50 m hoog. Bereken de geleverde arbeid.
6
Een blok wordt met een kracht van 120 N over een afstand van 150 m voortgetrokken.
Bereken de arbeid door deze kracht geleverd, als kracht en verplaatsing:
- dezelfde richting en zin hebben;
- een hoek van 31,4° insluiten.
7
Een ophaalkraan verricht een arbeid van 36. 105J om een massa van 4000 kg op te tillen.
Bereken de hoogte waarover de massa verplaatst werd.
8
Een tractor trekt een schip op een kanaal voort. De kabel, die de tractor met het schip
verbindt, sluit met de as van het kanaal een hoek van 20,0° in. De tractor trekt met een
kracht van 45.102 N. De boot verplaatst zich, vo1gens de as van het kanaal, over een
afstand van 650m. Bereken de geleverde arbeid.
9
Een auto start met een versnelling van 0,75m/s² voor een rit van 40s op een rechte weg. De
massa is 1200 kg. Bereken de arbeid tijdens deze rit op de auto geleverd.
10
Een wagen met een massa van 1200kg rijdt tegen een sne1heid van 72,0 km/h. P1ots remt
de bestuurder en komt in 10,0s tot sti1stand. Bereken de grootte van de inwerkende kracht,
en de geleverde arbeid tijdens het remmen.
11
De kracht die op een deeltje inwerkt, verandert als functie
van de plaats zoals op de figuur getekend. Bepaal de
arbeid door de kracht geleverd als het deeltje beweegt:
a) van x = 0m tot x = 8m,
b) van x = 8m tot x = 10m,
c) en van x= 0m tot x= l0m.
12
De kracht verandert als functie van de plaats volgens de betrekking: F ( x)  3.x 2  5 .
Bereken de ontwikkelde arbeid op een voorwerp als het beweegt van x = 4,0 m tot x = 7,0
m.
13
Indiana Jones komt in het midden van een moeras terecht. Om in de X-richting uit het
moeras te komen, wordt verondersteld dat de getalcomponent van zijn ontwikkelde kracht
voldoet aan de betrekking: F ( x)  1000  2,5.x 2
a) Maak de F(x)-grafiek.
b) Als Indiana Jones een afstand van x = 20 m moet afleggen om uit het moeras te
geraken, hoe groot is dan zijn geleverde arbeid?
c) Bereken de grootte van zijn gemiddelde kracht om uit het moeras te geraken.
14.
Hoeveel arbeid verricht de gravitatiekracht op een raket van 20ton als deze beweegt van op
de aarde tot op een hoogte van 400km? We nemen aan dat de massa van de raket constant
blijft.
m .m
Fg  G. 1 2 2 , met Fg negatief omdat deze tegen de verplaatsing in is gericht.
r
15
Bewijs dat de arbeid geleverd door de zwaartekracht onafhankelijk is van het gevolgde
traject:
Tip: Verdeel het tweede traject in twee stukken.
16
Een luchtbel van 10-5m² bevindt zich op een diepte van 10m. Boven het wateroppervlak
heerst er een druk van 1000hPa. Bereken de arbeid geleverd door de Archimedeskracht
geleverd gedurende het hele proces van opstijgen ( x  0m  x  10m ).
F  x   .g .
p0 .V0
p atm  .g .(h  x)
17
Een trein van 450 ton rijdt tegen een sne1heid van 54.0 km/h. Welke snelheid zou een
vrachtwagen van 50,0 ton moeten kunnen ontwikkelen om een energie te verkrijgen die
even groot is?
18
Een vallend rotsb1ok heeft. op het ogenblik dat het de grond raakt, een kinetische energie
van 100. 104 J. De grootte van de snelheid waarmee het de grond raakt. is 50,0 m/s.
Bereken hieruit de massa van het rotsblok.
19
Een kracht met een grootte van 30,0 N versnelt een voorwerp van 20,0 kg uit rust over een
afstand van 3,00 m over een glad horizontaal oppervlak. Bereken hieruit de kinetische
energie van dit voorwerp na het afleggen van die afstand.
20
Een plat cilindervormig blokje van 100 g voert door middel van een touwtje een eenparige
cirkelbeweging uit op een glad horizontaal oppervlak. De spankracht in het touw bedraagt
0,98 N en de straal van de cirkel 50 cm. Hoe groot is de kinetische energie van het blokje?
21
Op een massa van 5,0 kg werkt in de X-richting een
kracht F. F(x) is in het nevenstaand diagram als functie
van de plaats voorgesteld.
Indien de massa vanuit rust vertrekt in y = 0,0 m,
bedraagt haar snelheid in het punt y = 6,0m?
22
Een automonteur duwt een auto van 2500 kg vanuit rust in beweging. Hij levert daarbij
over een afstand van 25,1 m een arbeid van 50.102 J. Hoe groot is de eindsnelheid van de
auto? Hoe groot is de horizontale kracht door de mecanicien uitgeoefend?
Houd geen rekening met de wrijving tussen de auto en de baan.
23
Bij een ballistische demonstratie vuurt een FBI-agent een kogel van 55 g horizontaal in een
hoop zand. De beginsnelheid van de kogel is 350 m/s en hij komt tot rust na 18 cm. Hoe
groot is de gemiddelde kracht die het zand op de kogel uitoefende?
24
Een massa van 6,4 kg wordt met een touw over een
afstand van 2,0 m omhoog getrokken. De spankracht in
het touw is 80 N.
d) Bereken de arbeid door de spankracht geleverd.
e) Bereken de arbeid door de zwaartekracht geleverd.
f) Hoe groot is de snelheid van de massa na deze
afstand, als ze vanuit rust vertrekt?
25
Een doos van 40,2 kg, oorspronkelijk in rust, wordt door een horizontaal uitgeoefende
kracht van 130 N over een afstand van 5,23 m voortgetrokken over een horizontale vloer.
De wrijvingsfactor bedraagt 0,300.
Bereken:
- de arbeid geleverd door de uitgeoefende kracht;
- de arbeid geleverd door de wrijvingskracht;
- de kinetische energie van de doos;
- de grootte van de snelheid van de doos.
26
Op een bevroren vijver krijgt een slede een trap, waardoor ze rechtlijnig beweegt met een
beginsnelheid van 2,3 m/s. De wrijvingsfactor tussen de slede en het ijs is 0,012. Welke
afstand legt de slede af voor ze tot rust komt?
27
Op een deeltje met een massa van 2,00 kg dat op de X-as beweegt, werkt een resulterende
kracht in F = 3 x² - 4 x + 5,2. Bereken de arbeid op het deeltje geleverd als het zich
verplaatst van x = 1,0 m tot x = 3,0 m.
Als de snelheid van het deeltje in y = 1,0 m gelijk is aan 5,2 m/s, hoe groot is ze dan in
x = 3,0m ?
2. Energie
1
Een kindje met een massa van 11,2 kg glijdt vanuit rust vanaf de top van een glijbaan naar
beneden. Hoe groot is de snelheid van het kind onderaan, in de veronderstelling dat de
glijbaan volkomen glad is en een hoogte van 6,50 m heeft?
2
De uitgestoten lava van de vulkaan Loki op de maan Io van de planeet Jupiter,
kan hoogten bereiken van 100 km. De gravitatieversnelling op de maan Io is
1,80 mIs2 en wordt constant verondersteld. Rond deze maan lo is er geen
atmosfeer aanwezig zodat er geen wrijvingsverliezen zijn. Hoe groot moet de
snelheid van de lava aan de kratermond zijn opdat deze hoogte van 100 km
zou bereikt worden?
a 600m/s;
b 180m/s;
C 20m/s;
d deze snelheid hangt af van de massa van de uitgestoten lavabrokken.
3
Fientje wil uit drie wrijvingsloze glijbanen, hieronder afgebeeld, deze kiezen die haar de
grootste snelheid bezorgt onderaan.
Als ze bovenaan steeds vanuit rust vertrekt, welke keuze moet ze dan maken?
a 1;
b 2;
c 3;
d om het even.
4
Twee gladde banen van gelijke lengte hebben 'deuken': bij A omhoog en bij B omlaag. Ze
hebben dezelfde kromming.
Als twee identieke ballen gelijktijdig en met dezelfde beginsnelheid starten, dan:
a zal bal a eerst aankomen;
b zal bal b eerst aankomen;
c zullen de ballen gelijktijdig aankomen;
d zal er niet kunnen voorspeld worden welke bal er eerst aankomt.
5
Een blok met massa m glijdt vanuit rust langs een gladde helling van een hoogte h naar
beneden. Onderaan botst het tegen een veer waardoor deze ingedrukt wordt. Over welke
afstand wordt de veer ingedrukt?
6
Bij de studie van de schuine worp werd de hoogte berekend die een lichaam kan bereiken:
2
v 0 . sin 2 
h
2.g
Leid deze formule af steunende op de energiebehoudswet.
7
Vanaf een hoogte van 10,0 m laat men een bal met een massa van 100 g naar beneden vallen.
Bij het botsen van de bal tegen de grond wordt 35 % van de mechanische energie omgezet in
warmte en vervormingsarbeid.
Hoe hoog botst de bal terug? Houd geen rekening met de luchtweerstand.
8
Op een hoogte van 3,00 m heeft een verticaal vallend voorwerp, met een massa van 0,200kg,
een snelheid van 12,0 m/s. Dit voorwerp botst op een horizontale vloer en bereikt daarna een
hoogte van 1,50 m. Verwaarloos de luchtweerstand. Hoeveel energie is er in
vervormingsarbeid en warmte omgezet bij de botsing met de vloer?
9
Bij een slingerproef heeft men een bolletje aan een draadje opgehangen en uit zijn
evenwichtsstand gebracht. Men laat het bolletje los, en als het de evenwichtsstand passeert, is
het 30,0 cm gezakt. Het passeert deze evenwichtsstand met een snelheid van 2,00 m/s.
Hoeveel % van de mechanische energie van het bolletje is er tijdens het dalen door de
weerstand met de lucht in andere energievormen, zoals warmte, omgezet?
10
Een metselaar wordt van stenen voorzien door zijn helper, die 3,0 meter onder hem staat en
die de stenen verticaal opgooit. Als de stenen een snelheid van 2,0 m/s hebben als ze de
metselaar bereiken, welk percentage van de aanvankelijke kinetische energie van de steen was
dan nutteloos? Houd geen rekening met de luchtweerstand.
a) Ongeveer 94%.
c) Ongeveer 25%.
b) Ongeveer75%.
d) Ongeveer 6%.
11
Praktisch elk pretpark bezit een waterbaan.
In Bobbejaanland is die zodanig geconstrueerd dat een wagentje van 500kg op 10,0m hoogte
een snelheid heeft van 15,0m/s. Na de waterplas kan het wagentje nog net een platform van
2,0m hoogte bereiken waar het tot stilstand komt.


Hoe groot is de kinetische energie voor en na de waterplas?
Kan je uit deze gegevens de grootte van de gemiddelde wrijvingskracht halen? Indien
niet, over welke gegevens zou men dan nog moeten beschikken?
12.
Een pijl wordt omhoog geschoten. Er is geen wrijving.
Hoe groot moet de snelheid zijn onderaan om op 10m hoogte met een snelheid van 5m/s in
een dak te schieten?
13.
Johan beklimt een rots. Hij verplaatst zich van x=0m tot x=120m. De kracht die hij uitoefent
is gelijk aan F ( x)  2.10 6.x 2  0,05.x  3 .
a) Bereken de toegenomen energie.
b) Zoek de hoogte van het eindpunt.
Deel 5: TRILLINGEN
1 Trillingen
1.2 De harmonische trilling
1.
Bereken de uitwijking na 1s, 2s, 3s, … 8s en 12s als:
a) A=0,04m T=8s 0=/4
b) A=0,05m T=12s 0=-/6
2.
Bepaal de amplitude, frequentie, periode en beginfase van de volgende HT’en:
y (cm)
4
2
0.5
1
1.5
2
2.5
3
t (s)
-2
-4
3.
Stel twee HT’en met identieke frequenties (1Hz) A1=1m en A2=2m voor in een y(t)-grafiek,
als
a)   0
b)   

c)  
2
4.
Gegeven een HT voorgesteld door:

y (t )  3. sin(2. .t  )
3
 Wat is de amplitude?
 Wat is de frequentie?
 Wat is de beginfase?
5.
Twee puntmassa’s beschrijven met dezelfde frequentie een harmonische trilling volgens
dezelfde lijn en met hetzelfde centrum. De ene is /2 rad in fase op de andere voor; hun
amplitudes zijn 120mm.
Op welke posities ‘ontmoeten’ ze elkaar?
1.4 Voorbeelden van harmonisch trillende systemen
1.4.1 De trilling van een massa aan een veer
1.
Hoe kun je de massa aan een veer in beweging brengen als de beginfase van de trilling gelijk
is aan respectievelijk 0, /2 rad?
2.
Welke waarde heeft de beginfase bij de volgende harmonische trillingen:
y (t )  A. cos( .t )
y (t )   A.sin( .t )
3.
Een veer wordt door een massa van 10,0 kg over 10,0 cm uitgerekt. Bereken de
eigenfrequentie van de trilling door deze massa om haar evenwichtsstand uitgevoerd.
4.
Een man van 75 kg staat op het uiteinde van een springplank. Dit uiteinde zakt hierbij 0,30 m
ten opzichte van zijn onbelaste stand. Indien de man nu zachtjes op en neer wipt, welke zal
dan de periode van de harmonische trilling zijn, die het uiteinde van de plank krijgt?
5.
Door aan een veer een massa van 10,0 kg te hangen wordt deze 1,00 cm uitgerekt. Men
vervangt deze massa door een van 100 kg en laat ze om haar evenwichtsstand trillen. Bereken
de frequentie.
6.
Een lange stalen bladveer is aan één zijde vastgeklemd zoals aangegeven
op de figuur. Aan de andere zijde is een bol bevestigd met een massa van
2,0 kg. Om deze bol een uitwijking uit de evenwichtsstand van 0,10 m te
geven is een kracht nodig van 4,0 N. Als de bol daarna wordt losgelaten
ontstaat een periodieke beweging. De periode van deze beweging is:
a) 0,71s;
b) 4,5s;
c) 28s;
d) 1,4s.
7.
Een stalen veer is 0,200 m lang, heeft een veerconstante van 20,0 N/m, werd verticaal
opgehangen en is belast met een massa die een zwaartekracht van 0,98 N ondervindt.
Bereken:
de massa die er aan hangt;
de uitrekking die daar een gevolg van is;
de periode van een opgewekte verticale harmonische trilling van die massa.
8.
De veren van een auto worden 4,00 cm ingedrukt als er 4 personen, met een gezamenlijke
massa van 280 kg, in gaan zitten. Het chassis heeft een totale massa van 950 kg. Bereken de
frequentie van de trilling die de volle auto uitvoert, nadat hij in een put in de baan gereden is.
1.4.3 De projectie van een ECB
1.
Maak het fasorendiagram van twee trillingen als hun faseverschil respectievelijk 0 rad en 
rad bedraagt.
2.
Twee puntmassa’s beschrijven met dezelfde frequentie een harmonische trilling volgens
dezelfde lijn en met hetzelfde centrum. De ene is /2 rad in fase op de andere voor; hun
amplitudes zijn 120mm.
Op welke posities ‘ontmoeten’ ze elkaar?
Wat is de maximale afstand tussen beide?
1.5 Energie van een systeem dat een HT uitvoert
1.
Een deeltje trilt harmonisch met een amplitude van 50,0 mm en een maximale snelheid van
0,250 m/s. Bereken de pulsatie, de periode en de maximale versnelling van het deeltje.
2.
De top van een been van een stemvork heeft een maximale snelheid van 4,00 m/s, terwijl hij
een harmonische trilling met een frequentie van 512 Hz uitvoert. Hoe groot is de amplitude?
3.
Een deeltje beschrijft een harmonische trilling met uitwijking:
y (t )  2,00. sin(3. .t )
- Bereken de pulsatie, de periode, de amplitude en de maximale snelheid.
- Zoek op het tijdstip t = 0,72 s de uitwijking, de snelheid en de versnelling.
4.
Een lichaam, dat een harmonische trilling uitvoert met een amplitude van 7,00 cm, bezit een
snelheid van 70,0 cm/s op het ogenblik dat de uitwijking
5,00 cm is. Zoek hieruit de periode van de trilling.
5.
Een massa van 0,100 kg voert een harmonische trilling uit waarbij de amplitude A = 0,050 m,
de pulsatie ω=3,14 s−1 en de fasehoek op bet begintijdstip 0=/8 rad bedragen.
Bereken:
a) de periode en de frequentie van de trillende massa;
b) op welk ogenblik de uitwijking respectievelijk maximaal en minimaal is;
c) de grootte van de snelheid op het ogenblik dat de uitwijking respectievelijk maximaal
en minimaal is;
d) de grootte van de versnelling op bet ogenblik dat de uitwijking respectievelijk
maximaal en minimaal is;
e) de mechanische energie van de massa.
6.
Beoordeel volgende uitspraak: 'Bij een harmonische trilling is de versnelling in absolute
waarde het kleinst als de snelheid in absolute waarde het grootst is.
7.
Een zuiger van een automotor voert een harmonische trilling uit met een amplitude van 5,0
cm. De massa van de zuiger is geluk aan 2,00 kg. Bereken de maximale grootte van de
snelheid en van de versnelling van de zuiger als de frequentie van de motor 3600 toeren/min
bedraagt.
8.
Het diagram geeft de plaats weer als functie van de tijd van een
deeltje dat een harmonische trilling uitvoert.
Als dezelfde tijdsschaal genomen wordt, dan is de snelheidscomponent van de snelheid van
het deeltje het best weergegeven op figuur:
9.
Een deeltje voert een HT uit. Op welke plaats(en) bereikt de snelheid haar grootste waarde?
Op welke plaats(en) is de snelheid twee keer kleiner dan de maximale snelheid?
10.
Een wagentje voert om bet punt q een periodieke beweging uit. Aan de ene kant beweegt het
tegen een helling op tot aan r, terwijl het aan de andere kant tegen een veer drukt tot aan p. De
afstanden pq en qr zijn ongeveer even groot. Er is geen wrijving.
In welke van de onderstaande figuren wordt de grootte van de snelheid als functie van de tijd
best weergegeven?
1.7 Samenstellen van trillingen
1.
Zoek de amplitude en beginfase van de samenstelling (op twee manieren)
1
0.5
0.2
0.4
0.6
0.8
1
1.2
1.4
y1
-0.5
-1
y2
y
2.
Zoek de amplitude en beginfase van de samenstelling (op twee manieren)
1.5
1
0.5
0.2
-0.5
y1
-1
y2
-1.5
y
0.4
0.6
0.8
1
1.2
1.4
3.
Voor welk faseverschil is de amplitude van de resulterende trilling bij het samenstellen van
twee trillingen met dezelfde frequentie het grootst? Wanneer is ze het kleinst? Bereken haar
grootte in beide gevallen.
4.
De volgende trillingen hebben dezelfde richting. Stel ze telkens samen, vectorieel en grafisch,
en bereken de resulterende trilling
a) A1=A2=3cm, T=12s, 01=0, 02=/3
b) A1=A2=3cm, T=12s, 01=0, 02=/6
c) A1=3cm, A2=4cm, T=12s, 01=0, 02=/3
d) A1=3cm, A2=4cm, T=8s, 01=0, 02=/3
5.
Stel drie HT’en met dezelfde trillingsrichting samen (vectorieel) indien ze dezelfde amplitude
en frequentie hebben, doch respectievelijk beginfasen van 0°, 120° en 240°.
6.
Een puntmassa is tegelijk onderworpen aan twee trillingen volgens dezelfde lijn. Hun
vergelijkingen zijn:
y1 (t )  0,050. sin(250. .t )
y 2 (t )  0,050. sin(240. .t )
a) Schrijf de bewegingsvergelijking op van de resulterende trilling.
b) Zoek de maximale en minimale amplitude van de trilling.
c) Bepaal de frequentie van de zwevingen.
7.
Beschouwen we de volgende trillingen met onderling loodrechte richtingen:
y1 (t )  A. sin( .t )

y 2 (t )  A. sin( 2. .t  )
4
Construeer de samenstelling.
2 Golven
2.2 Begrippen
1.
Vanuit een vuurtoren ziet men de zeegolven aankomen met een snelheid van 10m/s. Er is een
afstand van 5,5m tussen twee opeenvolgende golftoppen. Bereken de frequentie en de
periode van deze golfbeweging.
2.
In een zwembad worden kunstmatig golven aangemaakt. Een paaltje wordt om de 5,0s
ondergedompeld door het water. De golflengte is 3,5m. zoek de golfsnelheid.
3.
Radio Donna zendt vanuit Brussel uit op een frequentie van 88,3MHz. Als de radiogolven
zich voortplanten met een snelheid van 2,99.108m/s, bereken dan de golflengte.
4.
Bereken de golflengte van een la (440Hz), als je weet dat de geluidssnelheid in lucht 340m/s
is.
5.
De vergelijking van een lopende golf is:
  t
x 
y  4.sin  2 
  
  0,2 10  
Bepaal de golflengte, de frequentie en de voortplantingssnelheid van de golf.
6.
Twee punten, op 30cm van elkaar gelegen, hebben bij een lopende golf in een koord een
faseverschil van 270°. Welke frequentie heeft de trilling die zich in het koord voortplant met
een snelheid van 3,6m/s?
7.
Een dobber trilt op stilstaand water. De veroorzaakte golven planten zich voort met een
snelheid van 0,80m/s en de golflengte bedraagt 30cm. Bereken de frequentie.
Geef de trillingsvergelijking van een punt op 2,4m van het storingscentrum als de amplitude
in dit punt 3,0cm is. Is dit punt in fase of in tegenfase met de bron?