Kracht en beweging

Domein D: Kracht en beweging
Subdomein: Krachten, rust en eenparige beweging
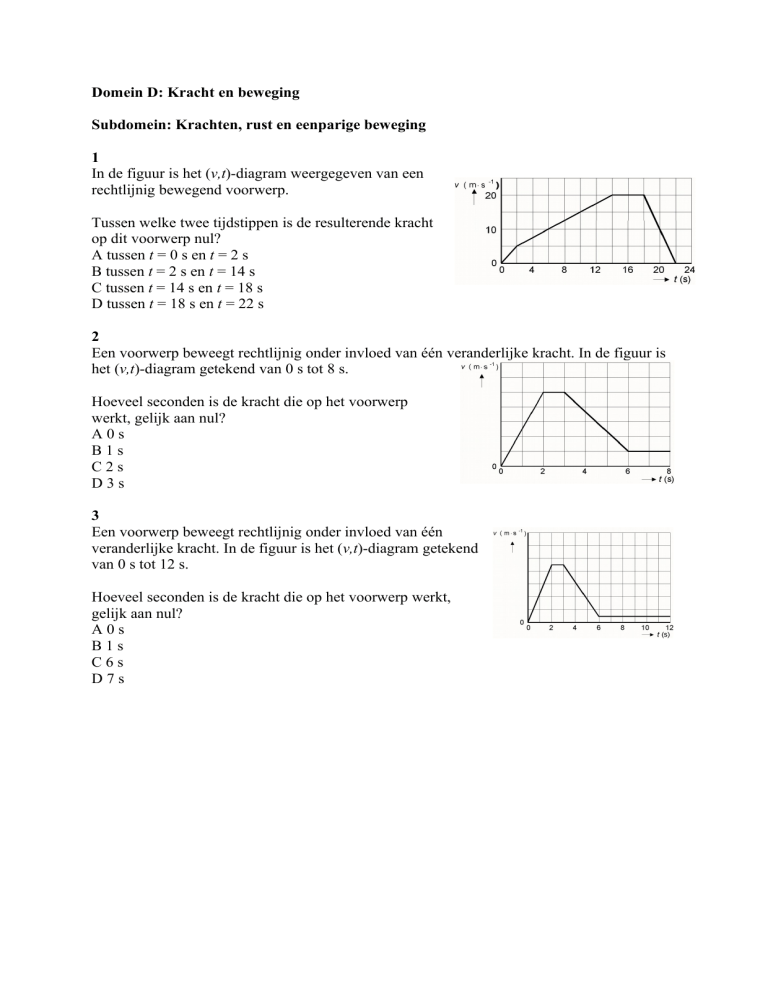
1
In de figuur is het (v,t)-diagram weergegeven van een
rechtlijnig bewegend voorwerp.
Tussen welke twee tijdstippen is de resulterende kracht
op dit voorwerp nul?
A tussen t = 0 s en t = 2 s
B tussen t = 2 s en t = 14 s
C tussen t = 14 s en t = 18 s
D tussen t = 18 s en t = 22 s
2
Een voorwerp beweegt rechtlijnig onder invloed van één veranderlijke kracht. In de figuur is
het (v,t)-diagram getekend van 0 s tot 8 s.
Hoeveel seconden is de kracht die op het voorwerp
werkt, gelijk aan nul?
A0s
B1s
C2s
D3s
3
Een voorwerp beweegt rechtlijnig onder invloed van één
veranderlijke kracht. In de figuur is het (v,t)-diagram getekend
van 0 s tot 12 s.
Hoeveel seconden is de kracht die op het voorwerp werkt,
gelijk aan nul?
A0s
B1s
C6s
D7s
4
In figuur 1 is het (x,t)-diagram van een
voorwerp P weergegeven. In figuur 2 is
het (x,t)-diagram van een voorwerp Q
weergegeven.
Wat weet je van de resulterende kracht
FP op voorwerp P en de resulterende
kracht FQ op voorwerp Q?
A
B
C
D
FP
FQ
is 0
is 0
is 0
is constant (≠ 0)
is constant (≠ 0) is constant (≠ 0)
is constant (≠ 0)
neemt toe
5
Op een tafel ligt een voorwerp van 0,50 kg. Een kracht van 3,0 N, verticaal omhoog, trekt aan
het voorwerp.
Wat is de grootte van de normaalkracht Fn?
A Fn = 7,9 N
B Fn = 4,9 N
C Fn = 3,0 N
D Fn = 1,9 N
6
Een voorwerp met een massa van 3,1 kg ligt op een tafel. Op het
voorwerp wordt een horizontale kracht van 40 N uitgeoefend.
Het voorwerp blijft in rust.
Welke pijl geeft de richting aan van de resulterende kracht die
de tafel op het voorwerp uitoefent?
A1
B2
C3
D4
7
Een voorwerp met een massa van 4,0 kg ligt op een hellend vlak met hellingshoek α, waarbij
sin α = 0,30. Om te voorkomen dat het voorwerp gaat bewegen, oefent men er een kracht F op
uit, evenwijdig aan de helling omhoog gericht.
De maximale wrijvingskracht bedraagt 4,0 N.
Wat is de minimale en wat is de maximale waarde van F?
A
B
C
D
minimale waarde van
F
0,0 N
7,8 N
7,8 N
11,8 N
maximale waarde van F
7,8 N
11,8 N
15,8 N
15,8 N
8
Een voorwerp met een massa van 5,0 kg ligt op een
hellend vlak met hellingshoek α, waarbij sin α = 0,20.
Om te voorkomen dat het voorwerp gaat bewegen,
oefent men er een kracht F op uit, evenwijdig aan de
helling omhoog gericht. De maximale wrijvingskracht
bedraagt 4,0 N.
Wat is de minimale en wat is de maximale waarde van F?
A
B
C
D
minimale waarde van
F
0N
5,8 N
5,8 N
9,8 N
maximale waarde van F
5,8 N
9,8 N
13,8 N
13,8 N
9
Op een hellend vlak (hellingshoek α met sin α = 0,60 en
cos α = 0,80) bevindt zich een voorwerp met een massa van
2,0 kg. Om te voorkomen dat het voorwerp gaat bewegen
wordt een kracht F op het voorwerp uitgeoefend. F is 10 N en
evenwijdig aan het vlak omhoog gericht.
Hoe groot is de wrijvingskracht Fw en welke richting heeft deze?
A
B
C
D
grootte van Fw richting van Fw langs de helling
1,8 N
omhoog
1,8 N
omlaag
5,7 N
omhoog
5,7 N
omlaag
10
Een blok P met een massa van 5,0 kg bevindt zich op een
hellend vlak (hellingshoek 30). Door een koord dat over een
pen loopt, is het met een ander blok Q met een massa van 2,0
kg verbonden.
De massa van het koord en de wrijving bij de pen worden
verwaarloosd. P glijdt met een constante snelheid langs het
vlak naar beneden.
Hoe groot is de wrijvingskracht die P ondervindt?
A 4,9 N
B 19,6 N
C 29,4 N
D 49,0 N
11
Een 2,0 m lange lijn is horizontaal gespannen. In het
midden van de lijn wordt een blok van 1,0 kg gehangen.
Het midden van de lijn daalt hierdoor 10 cm. Het blok is
dan in rust.
Hoe groot is de spankracht in de belaste lijn?
A 4,9 N
B 9,8 N
C 49 N
D 98 N
12
Een voorwerp P is opgehangen aan twee even lange draden v en w, die aan een horizontaal
plafond zijn bevestigd. De figuur is op schaal getekend. De massa van de draden wordt
verwaarloosd. De zwaartekracht op het voorwerp P bedraagt 24 N.
Hoe groot is de spankracht in de ophangdraden?
A 12 N
B 15 N
C 24 N
D 30 N
13
Aan een koord van 50 cm lengte hangt een voorwerp P. Het
ophangpunt is O. De massa van het koord wordt
verwaarloosd. Onder invloed van een horizontale kracht F van
60 N gaat P 30 cm naar links en 10 cm omhoog. De figuur laat
de nieuwe evenwichtsstand zien.
Hoe groot is de massa van P?
A 6,1 kg
B 7,7 kg
C 8,2 kg
D 9,8 kg
14
Een voorwerp P is opgehangen aan twee
even lange draden v en w, die aan een
horizontaal plafond zijn bevestigd. De
draden maken een hoek van 150 met
elkaar. De massa van de draden wordt
verwaarloosd. De zwaartekracht op het
voorwerp P bedraagt 20 N.
Hoe groot is de spankracht in de ophangdraden?
A 10 N
B 21 N
C 39 N
D 77 N
15
Een blokje glijdt langs een ruwe helling naar beneden. In de
tekening hiernaast heeft men de krachten die op het blokje
werken getekend. Hierbij is Fz (vector 1) ontbonden in de
vectoren 2 en 3.
Welke vectoren moet je bij elkaar optellen om de resulterende
kracht op het blokje te krijgen?
A vector 1, 3 en 5
B vector 1, 4 en 5
C vector 2, 3 en 4
D vector 2, 3 en 5
16
Op een tafel ligt een voorwerp P. Op P werken (evenwijdig aan
het tafelblad) drie krachten van respectievelijk 3,0, 4,0 en 6,0 N.
Bovendien werkt op P een wrijvingskracht die maximaal 2,0 N
bedraagt.
Hoe groot is de resulterende kracht op P?
A 9,0 N
B 11 N
C 13 N
D 15 N
17
Een homogene staaf van 1,0 kg is vrij draaibaar in punt P en
wordt door een touw in de horizontale stand gehouden. De massa
van het touw wordt verwaarloosd. In punt P wordt door de muur
een kracht op de staaf uitgeoefend.
Welke pijl in de figuur geeft de richting van deze kracht het best
weer?
A pijl 1
B pijl 2
C pijl 3
D pijl 4
18
Op welke volgende wijze kan de joule in grondeenheden worden uitgedrukt?
A kg · m2 · s
B kg · m2 · s-2
C kg · m · s-2
D kg2 · m · s-1
19
Een karretje van 2,0 kg staat aan de voet van een helling van 30. Men trekt het 3,0 m langs
het vlak omhoog.
Hoeveel arbeid verricht de zwaartekracht daarbij?
A -59 J
B -29 J
C +29 J
D +59 J
20
Drie personen (1, 2 en 3) verplaatsen alle drie een even zware emmer van de begane grond
naar het dak van een huis.
Persoon 1 draagt de emmer via een ladder omhoog.
Persoon 2 staat op het dak en hijst de emmer met behulp van een touw omhoog.
Persoon 3 staat beneden en hijst de emmer met behulp van een takel omhoog.
We verwaarlozen alle wrijvingskrachten en het gewicht van de touwen en de takel.
De kleinste hoeveelheid arbeid wordt verricht
A uitsluitend door persoon 2.
B uitsluitend door persoon 3.
C door de personen 1 en 2.
D door de personen 2 en 3.
21
Een bal wordt verplaatst van de vloer naar een rek dat zich boven de vloer bevindt. Het
gewicht van de bal is 10 N. Om de arbeid te kunnen berekenen die voor deze verplaatsing
nodig is, heeft men nog een gegeven nodig, namelijk
A de massa van de bal.
B de hoogte van het rek.
C de tijd gedurende welke de bal verplaatst wordt.
D de snelheid waarmee de bal verplaatst wordt.
22
Een jongen met een massa van 60 kg brengt langs een ladder 20 kg stenen op 5 m boven de
grond. Een man hijst met een takel 50 kg stenen tot een hoogte van 6 m omhoog. De wrijving
wordt verwaarloosd.
Welke bewering over de hoeveelheid arbeid die beide personen verrichten, is juist?
A De man verricht meer arbeid dan de jongen.
B De man verricht evenveel arbeid als de jongen.
C De man verricht minder arbeid dan de jongen.
D Men kan niet zeggen wie de meeste arbeid verricht, omdat de massa van de man niet
gegeven is.
23
Twee even zware vrachtauto's P en Q moeten elk eenzelfde vracht 100 m omhoog brengen.
De wrijving met de weg en de lucht is voor beide vrachtauto's gelijk. Het vermogen van
vrachtauto P is groter dan het vermogen van vrachtauto Q.
Gegeven zijn onderstaande beweringen.
1 Vrachtauto P zal de vracht sneller omhoog kunnen brengen dan vrachtauto Q.
2 Vrachtauto P zal minder arbeid verrichten dan vrachtauto Q.
Welke van deze beweringen is juist?
A zowel 1 als 2
B alleen 1
C alleen 2
D geen van beide
24
Iemand tilt in 2 s een koffer met een massa van 20 kg van de grond af, op een kast die 1,5 m
hoog is.
Welke van onderstaande uitspraken is onjuist?
A Als de koffer op de kast staat, levert de kast een reactiekracht van 196 N.
B De kast verricht arbeid om de koffer op de kast te laten staan.
C Met deze gegevens kun je de energie berekenen die nodig is om de koffer op de kast te
zetten.
D Met deze gegevens kun je het geleverde vermogen van de persoon berekenen.
25
Een hijskraan heeft een vermogen van 1,5 · 10³ W.
Hoeveel tijd is er nodig om een hoeveelheid stenen met een totale
massa van 3,0 ·10² kg 51 m omhoog te hijsen?
A 1,0 · 10-1 s
B 1,0 · 101 s
C 1,0 · 10² s
D Dit is niet te berekenen.
26
Een hijskraan heeft een vermogen van 1,5 kW. Men wil een partij
stenen met een totale massa van 300 kg ophijsen.
Met welke maximale snelheid kan de kraan de stenen omhoog
hijsen?
A 0,51 m/s
B 1,0 m/s
C 3,1 m/s
D 5,1 m/s
27
Een takel die wordt aangedreven door een elektromotor kan in 20 seconden een voorwerp met
een massa van 100 kg, 10 meter omhoog hijsen.
Het vermogen van de elektromotor bedraagt
A 49 W
B 0,49 kW
C 19,6 kW
D 196 kW
28
Een hijskraan brengt een massa van 400 kg in 20 seconden 5,1 meter omhoog.
De motor van de hijskraan heeft dan een vermogen geleverd van
A 1,0 · 10² W
B 1,0 · 10³ W
C 2,0 · 10³ W
D 2,0 · 104 W
29
In de figuur is een koevoet getekend. Dat is een stuk
gereedschap waarmee een spijker uit een plank gehaald
kan worden. Daartoe wordt op de koevoet in punt P een
kracht uitgeoefend. De pijltjes geven richtingen aan. De
massa van de koevoet wordt verwaarloosd.
In welke richting moet de kracht staan opdat deze zo klein
mogelijk is om de spijker er uit te halen?
A pijl 1
B pijl 2
C pijl 3
D pijl 4
30
In een L-vormige inhomogene plaat zijn gaten geboord, waardoor de plaat op verschillende
manieren aan een pen kan worden opgehangen. In
figuur 1 zijn twee evenwichtsstanden van de plaat te
zien. De wrijving wordt verwaarloosd.
In welke van de onderstaande figuren is de plaat ook in
een evenwichtsstand?
31
Twee homogene bollen van 2,0 kg en 1,0 kg zijn verbonden meteen starre staaf waarvan de
massa wordt verwaarloosd. Het geheel wordt op een steunpunt geplaatst zodat de staaf zich in
de horizontale stand bevindt en in evenwicht is.
In welk van de getekende punten moet het steunpunt dan geplaatst worden?
A punt P
B punt Q
C punt R
D punt S
32
Een bezem wordt door een vinger
ondersteund en is in evenwicht. De massa
van het deel van de bezem dat zich in de
figuurlinks van de vinger bevindt bedraagt
mL, de massa van het rechterdeel mR.
Welke conclusie betreffende mL en mR is juist?
A mL< mR
B mL= mR
C mL> mR
D Er is geen conclusie te trekken.
33
Om een caravan in evenwicht te houden moet men in punt P
een verticale kracht uitoefenen van 120 N. In plaats van P kan
ook in Q een verticale kracht F uitgeoefend worden om de
caravan in evenwicht te houden. De tekening is op schaal.
Hoe groot is de kracht F in Q?
A 80 N
B 120 N
C 150 N
D 180 N
34
Een homogeen blok kan niet over de horizontale vloer glijden. Het kan
wel gekanteld worden. Om het blok te laten kantelen wordt een kracht
F uitgeoefend van 50 N. Slechts in één van de getekende situaties blijkt
het blok te kantelen.
In welke situatie is dat?
35
Een balk PQ is verticaal opgesteld en kan om Q draaien. De
zwaartekracht op de balk is 100 N en de kracht F, die in Pop de
balk werkt, is 50 N. De aan de balk bevestigde kabel zorgt voor
evenwicht. De massa van de kabel wordt verwaarloosd.
Hoe groot is de kracht die in Q op de balk werkt?
A 100 N
B 112 N
C 125 N
D 175 N
36
Een rechthoekig blok van 30 kg ligt horizontaal op de grond.
Een stang van 2,0 kg is star aan dit blok verbonden. De
tekening geeft de situatie op schaal. Op het uiteinde van de
stang wordt een horizontale kracht F uitgeoefend. Het blok
gaat niet schuiven.
Hoe groot moet kracht F zijn opdat het geheel op het punt staat
te kantelen?
A 98 N
B 109 N
C 118 N
D 127 N
37
Een homogene lat is draaibaar om een vaste as door S.
Het gewicht van de lat bedraagt 100 N. Bekijk onderstaande vier evenwichtsituaties, waarin
soms gebruik gemaakt wordt van één of meer katrollen K. Verwaarloos de wrijving.
In welke van bovenstaande situaties is de kracht op de lat in S het kleinst?
A in situatie 1
B in situatie 2
C in situatie 3
D in situatie 4
38-a
De druk in een stoomketel kan worden geregeld met een hefboom KL. De figuur is op schaal.
In welke van onderstaande figuren zijn de drie krachten die de hefboom in evenwicht houden,
het best getekend?
38-b
De ballast oefent een kracht van 50,0 N op de staaf KL uit. De massa van de staaf KL en de
stop wordt verwaarloosd. De hefboom is in evenwicht. De as in K oefent een verticale kracht
op de staaf uit.
Hoe groot is deze kracht en hoe is hij gericht?
A 150 N, omhoog gericht
B 150 N, omlaag gericht
C 200 N, omhoog gericht
D 200 N, omlaag gericht
39
In de figuur is een staaf PR getekend die in P scharnierend is bevestigd.
In Q werkt een verticale kracht FQ omhoog en in R een verticale kracht FR omlaag, zodat de
staaf in evenwicht is.
De massa van de staaf wordt verwaarloosd.
Men verandert de kracht in R. Om de staaf in evenwicht te houden moet de kracht in Q dan
ook veranderen.
Welk diagram geeft het verband tussen de grootte van FQ en die van FR het best weer?
40
Een starre staaf PQ is horizontaal ingeklemd in P en wordt in het midden M ondersteund. De
lengte van PQ is 4,0 m.
Op een afstand x van P hangt een massa R. De zwaartekracht op massa R bedraagt 10 N.
In P ondervindt de staaf een verticaal gerichte kracht FP.
De grootte en de richting van FP hangen af van x.
In een diagram wordt FP uitgezet als functie van x.
Daarbij wordt een omhoog gerichte kracht aangegeven met een positieve waarde van FP en
een omlaag gerichte kracht met een negatieve waarde.
In welk diagram wordt de kracht FP als functie van x juist weergegeven?
41
Een starre staaf PQ is horizontaal ingeklemd in P en wordt in het midden M ondersteund. De
lengte van PQ is 4,0 m.
De massa van de staaf PQ wordt verwaarloosd.
Op een afstand x van P hangt een massa R. De zwaartekracht op massa R bedraagt 10 N.
In P en M ondervindt de staaf een verticaal gerichte kracht van respectievelijk FP en FM. De
grootte en de richting van FP en FM hangen af van x.
In een diagram worden FP en FM uitgezet als functie van x.
Daarbij wordt een omhoog gerichte kracht aangegeven met een positieve waarde van F en een
omlaag gerichte kracht met een negatieve waarde.
In welk diagram worden de krachten FP en FM als functie van x juist weergegeven?
42
In een kruiwagen van 25 kg ligt een berg aarde met een
massa van 90 kg. Het zwaartepunt van het geheel is Z.
Hoe groot is de kracht die voor evenwicht in P verticaal
omhoog moet worden uitgeoefend?
A 3,5 · 10² N
B 5,0 · 10² N
C 7,8 · 10² N
D 2,5 · 10³ N
43
Jan houdt een spijkertje vast met een tang.
Hij knijpt bij de punten P en Q met een
kracht van 3,5 N.
Hoe groot is de kracht op het spijkertje?
A 1,3 N
B 2,1 N
C 5,8 N
D 9,3 N
44
Om een fles te openen moet bij de
kroonkurk een kracht F van 60 N omhoog
worden uitgeoefend. De afstand l1 = 2,0 cm,
de afstand l2 = 7,0 cm.
Hoe groot is de kracht die aan het uiteinde
moet worden uitgeoefend en in welke
richting moet deze worden uitgeoefend?
A
B
C
D
grootte
17 N
17 N
24 N
24 N
richting
omhoog
omlaag
omhoog
omlaag
45
Op een nijptang wordt een spierkracht F van
200 N uitgeoefend.
Hoe groot is de kracht die P van de nijptang
ondervindt?
A 2,2 kN
B 3,2 kN
C 4,8 kN
D 5,4 kN
46
Een verticaal opgestelde balk PQ kan in Q vrij draaien.
In P werkt op de balk een horizontaal gerichte kracht F
van 1,2 kN. Een aan de balk bevestigde kabel zorgt voor
evenwicht. De massa van de kabel is te verwaarlozen.
In de figuur is de situatie op schaal getekend.
Hoe groot is de spankracht in de kabel?
A 0,9 kN
B 1,5 kN
C 2,0 kN
D 2,5 kN
47
Een balk moet horizontaal opgesteld worden aan een muur. Het
einde S is aan de muur bevestigd en kan daar vrij draaien. Er moet
nog een kabel tussen balk en muur bevestigd worden.
De kabel kan aan de punten K, L, M en N bevestigd worden. De
massa van de kabel wordt verwaarloosd. Tussen welke twee punten
moet de kabel bevestigd worden opdat de spankracht in de kabel zo
klein mogelijk is?
A K en M
B K en N
C L en M
D L en N
48
Een niet-homogene lat ST is vrij draaibaar om S. De zwaartekracht op de lat bedraagt 10 N.
In P wordt op de lat een horizontaal gerichte kracht F uitgeoefend. De lat is in rust en maakt
een hoek van 30 met het horizontale vlak. Het zwaartepunt van de lat bevindt zich in Z.
SP = PZ = ZT.
Hoe groot is de kracht F?
A 12 N
B 17 N
C 20 N
D 35 N
49
Twee schijven zijn op elkaar geplakt en kunnen draaien om een gemeenschappelijke as. De
straal van de grote schijf is 5 × zo groot als die van
de kleine. Om de kleine schijf is een touw T1
geslagen waaraan met een kracht van 60 N
getrokken wordt. Aan de as is een touw T2
bevestigd. De spankracht in T2 en de wrijvingskracht met de grond beletten de schijven te
gaan bewegen.
Hoe groot is de spankracht in T2 ?
A 48 N
B 72 N
C 240 N
D 360 N
50
Een massa van 100 kg wordt opgetakeld via een touw dat over een losse en een vaste katrol is
geslagen. Daarvoor is een kracht F nodig.
Hoe groot is F?
A 2,45 · 10² N
B 4,90 · 10² N
C 9,80 · 10² N
D 19,6 · 10² N
51
Twee schijven zijn op elkaar geplakt en kunnen draaien om een
gemeenschappelijke as. De straal van de grote schijf is 2 × zo groot als die
van de kleine. Om de twee schijven zijn touwen gewikkeld met aan elk een
blokje. De zwaartekracht op het blokje P is 2,0 N. De massa van de touwen
en de schijven wordt verwaarloosd, evenals de wrijving. Het geheel is in
rust.
Hoe groot is de kracht die de as op het tweetal schijven uitoefent?
A 0,0 N
B 2,0 N
C 4,0 N
D 6,0 N
52
In de figuur is het aandrijfmechanisme van
een fiets schematisch weergegeven. De
tandwielen hebben stralen van 10 en 5,0 cm.
Het achterwiel heeft een straal van 30 cm. De
trapper is 15 cm lang en staat horizontaal.
Terwijl de fiets wordt vastgehouden, oefent
men op het pedaal een kracht van 6,0 N uit,
recht naar beneden. Daardoor oefent het wiel
een wrijvingskracht op de weg uit.
Hoe groot is deze wrijvingskracht?
A 1,5 N
B 3,0 N
C 12 N
D 24 N
53
Welke van de onderstaande eenheden is geen eenheid van energie?
A watt (W)
B joule (J)
C newtonmeter (Nm)
D kilowattuur (kWh)
54
Een man duwt een kar over een klinkerweg. Na enige tijd gaat
de klinkerweg over in een zandweg, de zandweg in een
asfaltweg en de asfaltweg gaat over in een betonweg. De
wrijving is niet te verwaarlozen.
De hele weg loopt horizontaal. Hiernaast is een diagram
getekend, waarin de spierkracht van de man als functie van de
weg is weergegeven.
Op welke weg verricht de man de meeste arbeid op de kar?
A klinkerweg
B zandweg
C asfaltweg
D betonweg
Subdomein: Energie en beweging
55
Twee krachten met een grootte van 12 N en 16 N, welke
onderling loodrecht op elkaar staan, werken op een voorwerp
van 4,0 kg.
Hoe groot is de versnelling die dit voorwerp krijgt?
A 1,0 m/s²
B 3,0 m/s²
C 5,0 m/s²
D 7,0 m/s²
56
Bekijk de onderstaande tikkerband.
Door de tijdtikker werden 50 stippen per seconde op de strook gezet.
De gemiddelde snelheid van het karretje tussen T en U is ongeveer
A 0,026 m/s.
B 0,065 m/s.
C 0,65 m/s.
D 1,3 m/s.
Stroboscopisch belichte kogelbaan
De figuur hiernaast stelt de stroboscopisch
belichte foto voor van een stuiterend
kogeltje dat vanuit O beweegt langs de
punten P, Q, ... U.
De tijd tussen twee opeenvolgende
lichtflitsen van de stroboscoop is 1 s.
Op tijdstip t = 0 s bevindt het kogeltje zich
in O.
Zijn baan wordt door de stippellijn
voorgesteld.
Bovenstaande gegevens horen bij de
volgende twee vragen.
57-a
Ga de volgende beweringen na.
1 Tussen t = 0 s en t = 6 s is de verplaatsing meer dan 15 m.
2 In R is de grootte van de snelheid 0 m/s.
Welke van deze beweringen is juist?
A zowel 1 als 2
B alleen 1
C alleen 2
D geen van beide
57-b
Noem de x-component en de y-component van de snelheid van het kogeltje op een bepaald
ogenblik vx en vy. Men beweert:
1 vx verandert tijdens de beweging
2 vy verandert tijdens de beweging
Welke van deze beweringen is juist?
A zowel 1 als 2
B alleen 1
C alleen 2
D geen van beide
58
In de figuur hiernaast is de grafiek van een relatie tussen de
grootheden plaats (x) en tijd (t) getekend.
Wat stelt de figuur voor?
A de veranderlijke beweging van een punt
B de baan van een rondgaand punt
C het (x,t)-diagram van een rondgaand punt
D de figuur kan onmogelijk het (x,t)-diagram van een bewegend
punt zijn
59
Een deeltje P beweegt langs een rechte lijn. Zijn
plaats als functie van de tijd wordt weergegeven in
de figuur. De verplaatsing van P in het tijdsinterval
van t = 0 s tot t = 6 s bedraagt
A -15 m.
B -10 m.
C -5 m.
D 25 m.
60
De tekening hiernaast stelt het (x,t)-diagram voor van een
rechtlijnige beweging.
Hoe groot is de verplaatsing van t = 0 s tot t = 8 s?
A2m
B3m
C5m
D meer dan 5 m
61
Punt P beweegt langs een rechte lijn.
Zijn plaats wordt gegeven door het (x,t)-diagram.
Hoe groot is de snelheid van punt P?
A -2 m/s
B -0,5 m/s
C 0,5 m/s
D 2 m/s
62
Onderstaande figuur stelt het (x,t)-diagram voor van twee fietsers P en Q die beiden op
dezelfde weg rijden.
In welk diagram is de afstand tussen de twee fietsers als functie van de tijd het best
weergegeven?
63
Van een rechtlijnige beweging is het (x,t)-diagram tussen
t = 0 s en t = 4 s gegeven.
Welke figuur geeft het (v,t)-diagram van deze beweging weer?
64
De plaatsfunctie van een punt dat op een rechte lijn beweegt
wordt gegeven door het (x,t)-diagram hiernaast.
Hoe groot is de gemiddelde snelheid van dit punt in het
interval [3 s;7 s]?
A -6 m/s
B -1,5 m/s
C +1,5 m/s
D +6 m/s
65
Een onweersbui verwijdert zich met
constante snelheid van een waarnemer. Deze
noteert gedurende 1 minuut het tijdsinterval
t tussen de bliksem en de bijbehorende
donderslag als functie van de tijd.
Onderstaande grafiek geeft zijn
waarnemingen weer.
Hij weet dat de geluidssnelheid 340 m/s is.
De snelheid van de bui is
A 0,02 m/s.
B 0,03 m/s.
C 6,8 m/s.
D 10,2 m/s.
66
De tekening hiernaast stelt het bovenaanzicht van een
tafelblad voor, waarop een bal rechtlijnig beweegt met
een snelheid van 5,0 m/s in de getekende richting.
Hoe groot is de tijd waarin de bal vanuit de getekende
stand rand I bereikt?
A 0,4 s
B 0,5 s
C 0,67 s
D 1,5 s
67
De beweging van een karretje wordt nagegaan met een tijdtikker. Door de tijdtikker worden
50 stippen per seconde op een strook papier gezet.
Een gedeelte van de strook ziet er als volgt uit:
De punten P, Q, R, S, T, U en V zijn
punten die een tijdsinterval hebben van
1/50 seconde.
De strook wordt geknipt en naast elkaar
geplakt.
Als we de punten Q, R, S, T, U en V door een lijn verbinden ontstaat een
A (v,t)-diagram.
B (x,t)-diagram.
C (a,t)-diagram.
D (x,t2)-diagram.
68
Een wandelaar loopt over een rechte weg. Het
verband tussen de snelheid van de wandelaar en de
tijd wordt weergegeven door het (v,t)-diagram van de
figuur hiernaast.
Welke combinatie van oppervlakten I en II komt
overeen met de verplaatsing van de wandelaar tussen
t = 0 en t = 16 s?
A 10 + 6 m
B 10 - 6 m
C 2(10 + 6) m
D 2(10 - 6) m
69
Een voorwerp beweegt langs een rechte lijn. Het verband tussen de snelheid van het voorwerp
en de tijd in de eerste tien seconden wordt weergegeven door onderstaand (v,t)-diagram.
Hoe groot is de verplaatsing van het voorwerp in de eerste tien
seconden?
A 2(12 - 8) m
B 12 - 8 m
C 2(12 + 8) m
D 12 + 8 m
70
De tekening hiernaast stelt het (v,t)-diagram van een
wandelaar voor.
In welk diagram is de plaats x van de wandelaar als
functie van de tijd t het best weergegeven?
71
Van een rechtlijnig bewegend deeltje is het (v,t)-diagram gegeven.
De berekening van de gemiddelde snelheid in m/s tussen
t = 0 s en t = 10 s is de volgende:
A
B
C
D
0,5  2
3

2
4
0,5 2
15
 
8
2
16
0,5  8  2  2
0
10
0,5  8  2  2 4

10
5
72
Een steen wordt verticaal omhooggeschoten. Van het eerste
gedeelte van zijn vlucht is het (v,t)-diagram getekend.
De afgelegde weg tussen t = 0 s en t = 4 s is dan
A 40 m.
B 80 m.
C 160 m.
D niet uit dit diagram te bepalen.
73
Een raket wordt verticaal omhoog geschoten. Gedurende de
vlucht van de raket heeft men een aantal gegevens verzameld
waardoor men het (v,t)-diagram kon tekenen (zie figuur
hiernaast).
Op tijdstip t = 40 s bevindt de raket zich
A op het startpunt.
B op zijn hoogste punt.
C halverwege tussen het startpunt en het hoogste punt.
D op geen der genoemde plaatsen.
74
Op een planeet valt een steen zonder beginsnelheid naar beneden van een hoogte van 80,0 m.
Na 7,1 s is de steen 40,0 m gevallen.
Na hoeveel seconden, gerekend vanaf het begin van vallen, treft de steen de grond?
A na 10,0 s
B na 12,5 s
C na 14,2 s
D na 18,2 s
75
Op een planeet valt een steen zonder beginsnelheid naar beneden van een hoogte van 80,0 m.
Na 5,0 s is de steen 20,0 m gevallen.
Na hoeveel seconden, gerekend vanaf het begin van vallen, treft de steen de grond?
A na 10,0 s
B na 12,5 s
C na 16,0 s
D na 20,0 s
76
Een steen valt in het luchtledige, zonder beginsnelheid naar beneden. Na t seconden heeft de
steen een afstand van 25 m afgelegd.
Na 2t seconden heeft de steen een afstand afgelegd van
A 50 m.
B 100 m.
C 125 m.
D 500 m.
77
Vanuit een punt Q wordt een bal horizontaal weggeworpen. Q
bevindt zich h meter boven een punt P (zie figuur). De bal
komt s meter van P op de grond terecht. Hierna wordt de bal
vanuit Q met een viermaal zo grote snelheid horizontaal
weggeworpen.
Op welke afstand van P komt de bal dan terecht?
Asm
B 2s m
C 4s m
D 16s m
78
Van een hoogte van 1,60 m wordt een geweerkogel horizontaal afgevuurd naar een even hoge
paal op 15,0 m van de schutter. De aanvangssnelheid van de kogel is 30,0 m/s,
Waar treft de kogel de paal?
A treft de paal niet, maar de grond vóór de paal
B 1,23 m onder de top
C 1,23 cm onder de top
D op zijn top
79
Een eenheid van energie is
A kg · m² · s
B kg² · m · s-1
C kg · m · s-²
D kg · m² · s-²
80
Een bal wordt omhoog gegooid. Iemand beweert dat tijdens de beweging omhoog
1 de kinetische energie van de bal wordt omgezet in zwaarte-energie van de bal;
2 de zwaartekracht arbeid verricht op de bal.
Welke van deze beweringen is juist?
A zowel 1 als 2
B alleen 1
C alleen 2
D geen van beide
81
Men laat een steen vallen van een hoogte van 60 m. De wrijving met de lucht wordt
verwaarloosd. Op een bepaald moment tijdens de val is de bewegingsenergie gelijk aan de
zwaarte-energie.
Op dat moment bevindt de steen zich op een hoogte van
A 0 m.
B 15 m.
C 30 m.
D 60 m.
82
Men laat een steen vallen van een hoogte van 60 m. De wrijving met de lucht wordt
verwaarloosd.
Op welke hoogte boven de grond is de bewegingsenergie 2 × zo groot als de zwaarte-energie?
A0m
B 10 m
C 20 m
D 30 m
83
Een kogel wordt met een beginsnelheid van 30 m/s in horizontale richting weggeschoten van
een 80 m hoge toren. De wrijving met de lucht wordt verwaarloosd.
Hoe groot is de snelheid van de kogel als hij de grond treft?
A 30 m/s
B 40 m/s
C 50 m/s
D 70 m/s
84
Een voorwerp valt in de lucht van een hoogte van 100 m naar beneden. In een diagram wordt
van dit voorwerp de som van de zwaarte-energie en de bewegingsenergie (Ez + Eb) uitgezet
tegen de hoogte. De wrijving van het voorwerp met de lucht wordt verwaarloosd.
In welk van bovenstaande diagrammen 1 t/m 4 is de relatie tussen Ez + Eb en de hoogte juist
weergegeven?
A in diagram 1
B in diagram 2
C in diagram 3
D in diagram 4
85
Een kogel wordt verticaal omhoog geschoten. De grootste hoogte die
de kogel bereikt, noemen we htop. Het diagram hiernaast geeft het
verband aan tussen de zwaarte-energie Ez en de hoogte h.
Welk diagram geeft het verband tussen de kinetische energie Ek en de
hoogte h van dezelfde beweging het best weer?
86
Een bal wordt vanaf de grond met een snelheid van 15 m/s recht
omhoog geschoten. Iemand wil de snelheid berekenen waarmee de
bal punt P op de terugweg zou passeren als er geen wrijving zou
zijn. Punt P ligt 5 meter van de grond. Hij gebruikt de wet van
arbeid en kinetische energie.
Welk gegeven heeft hij naast bovenstaande gegevens ook nog nodig?
A de massa van de bal
B de plaats van het hoogste punt
C de tijd, die de bal erover doet om punt P te bereiken
D geen
87
In onderstaand diagram heeft men van een voorwerp de
zwaarte-energie Ezw uitgezet tegen de hoogte. Men brengt het
voorwerp vanaf een bepaalde hoogte naar een maal zo grote
hoogte.
Uit het diagram volgt dat de zwaarte-energie dan
A hetzelfde zal blijven.
B 2 maal zo groot zal worden.
C 3 maal zo groot zal worden.
D groter zal worden, maar hoeveel maal is niet af te leiden,
want de massa van het voorwerp is niet gegeven.
88
Twee kogeltjes P en Q bevinden zich op dezelfde hoogte boven de grond. Op hetzelfde
moment dat men P laat vallen, schiet men Q met een horizontale beginsnelheid weg.
De wrijving wordt verwaarloosd.
Beoordeel de volgende uitspraken:
1 P en Q treffen tegelijk de grond.
2 P en Q treffen de grond met even grote snelheid.
Welke van deze uitspraken is juist?
A zowel 1 als 2
B alleen 1
C alleen 2
D geen van beide
89
Auto P met een massa van 1000 kg heeft een snelheid van 100 km/h. Auto Q met een massa
van 500 kg heeft een snelheid van 50 km/h.
Hoe groot is de kinetische energie van auto P ten opzichte van de kinetische energie van auto
Q?
A 8× zo groot als die van auto Q
B 4× zo groot als die van auto Q
C gelijk aan die van auto Q
D de helft van die van auto Q
90
De kogels P, Q en R hebben dezelfde massa. Kogel P wordt van een hoge toren verticaal
omlaag geworpen met beginsnelheid. Kogel Q laat men van dezelfde toren vallen, zonder
beginsnelheid.
Kogel R wordt van dezelfde toren horizontaal weggeworpen.
In welk geval is de arbeid die door de zwaartekracht tijdens het vallen wordt verricht het
grootst?
A bij kogel P
B bij kogel Q
C bij kogel R
D bij alle drie de kogels even groot
91
Een auto rijdt met constante snelheid een helling op.
Bekijk onderstaande beweringen over de zwaarte-energie en bewegingsenergie van de auto.
1 De zwaarte-energie van de auto neemt toe.
2 De bewegingsenergie van de auto neemt toe.
Welke van deze beweringen is juist?
A zowel 1 als 2
B alleen 1
C alleen 2
D geen van beide
92
Een voorwerp P met een massa van 1 kg bevindt zich 20 meter boven de grond.
Een voorwerp Q met een massa van 4 kg bezit evenveel zwaarte-energie als voorwerp P.
Hoeveel meter bevindt het voorwerp Q zich boven de grond?
A 5 meter
B 16 meter
C 20 meter
D 80 meter
93
Voorwerp P heeft een grotere massa dan voorwerp Q. In hetzelfde diagram zet men van elk
van beide voorwerpen de zwaarte-energie uit tegen de hoogte. Men krijgt dan één van de
onderstaande diagrammen.
Voor beide voorwerpen is de relatie tussen de zwaarte-energie en de hoogte juist weergegeven
in
A diagram 1.
B diagram 2.
C diagram 3.
D diagram 4.
94
Een voorwerp met een massa van 5,1 kg beweegt
langs een helling van P via Q naar R. In R is zijn
zwaarte-energie 1,0 · 10² J groter dan in P.
Welke van onderstaande hellingen met de punten
P, Q en R voldoet aan dit gegeven?
A Beide hellingen.
B Alleen de helling in figuur I.
C Alleen de helling in figuur II.
D Geen van beide hellingen.
95
Een kogel met een massa van 1,0 kg hangt aan een koord met
een te verwaarlozen massa. De lengte van het koord bedraagt
1,60 m. Men geeft de kogel een uitwijking en laat de kogel
dan los (zie figuur).
Hoe groot is de maximale snelheid die de kogel krijgt?
A 2,8 m/s
B 4,0 m/s
C 5,7 m/s
D 16 m/s
96
Van een systeem van twee veren is in het diagram het verband
weergegeven tussen de belasting en de uitwijking.
Dit systeem van veren is 5,0 cm uitgetrokken.
Hoeveel arbeid is hierbij verricht?
A 11 · 10-2 J
B 15 · 10-2 J
C 19 · 10-2 J
D 30 · 10-2 J
97
Een blokje met een massa van 2,0 kg wordt op
een helling losgelaten in P en blijkt dan door
de wrijving niet verder te glijden dan tot R (zie
figuur). De afstanden zijn in de figuur
aangegeven.
A
B
C
D
de totale arbeid door de
wrijvingskracht verricht, is
-19,6 J
-19,6 J
-39,2 J
-39,2 J
de gemiddelde
wrijvingskracht is
3,3 N
3,9 N
6,5 N
7,8 N
98
Een voorwerp met een massa van 2 kg heeft een snelheid van 4 m/s. Op dit
voorwerp werkt gedurende korte tijd een kracht, waardoor dit voorwerp
een andere snelheid krijgt.
Tekening I geeft de snelheidsvector voordat de kracht werkt.
Tekening II geeft de snelheidsvector nadat de kracht heeft gewerkt.
Hoe groot was de arbeid die de kracht op het deeltje heeft uitgeoefend?
A1J
B3J
C6J
D9J
99
Een kogel van 8,0 kg heeft op een bepaald tijdstip een snelheid van 40 m/s in horizontale
richting en een snelheid van 30 m/s in verticale richting.
Hoe groot is de kinetische energie van de kogel op dat tijdstip?
A 3,6 · 103 J
B 6,4 · 103 J
C 10 · 103 J
D 20 · 103 J
100
Hieronder staan drie glijbanen getekend, die alle eindigen in Q. Het beginpunt P van alle
glijbanen is even hoog. Ook alle eindpunten Q liggen even hoog boven de grond.
Een jongen wil met een zo groot
mogelijke snelheid in punt Q de
glijbaan afkomen. De wrijving wordt
verwaarloosd.
Om een zo groot mogelijke snelheid in Q te bereiken zal de jongen
A glijbaan 1 moeten kiezen.
B glijbaan 2 moeten kiezen.
C glijbaan 3 moeten kiezen.
D elke glijbaan kunnen kiezen, want zijn snelheid in Q is bij alle glijbanen even groot.
Skischans
De figuur stelt een skischans voor. De skiër
beweegt zich volgens de door de stippellijn
aangegeven baan. Bij punt 4 raakt hij de
grond. Hierna remt hij af zodat hij in punt 6
stilstaat.
Beantwoord nu de volgende twee vragen.
101-a
De bewegingsenergie van de skiër is het grootst in
A punt 1.
B punt 2.
C punt 3.
D punt 4.
101-b
De zwaarte-energie van de skiër neemt toe
A van punt 1 naar punt 2.
B van punt 2 naar punt 3.
C van punt 3 naar punt 4.
D van punt 4 naar punt 6.
102
PQR stelt een gekromde goot voor. Men laat bij P een knikker los.
Die glijdt naar beneden en verlaat de goot bij R. De knikker
beschrijft daarna de gestippelde baan.
De wrijving wordt verwaarloosd. Welke uitspraak over de
kinetische energie van de knikker is juist?
A Deze is bij S groter dan bij R.
B Deze is bij S gelijk aan nul.
C Deze is bij Q en R even groot.
D Deze is bij R groter dan bij S.
103
Een kogel rolt heen en weer in een put, zoals is
aangegeven in de tekening. De kogel verlaat de put niet.
De wrijving van de kogel met de lucht en met de wand
van de put wordt verwaarloosd. De totale energie van de
kogel (de som van de zwaarte-energie en de
bewegingsenergie) is
A het grootst in punt X.
B het grootst in punt Y.
C het grootst in punt Z.
D in alle punten even groot.
104
Een honkballer krijgt een bal van 400 g toegeworpen, die
een snelheid van 10,0 m/s heeft. Hij raakt hem gedurende
0,010 s met het gevolg dat de bal in tegengestelde richting
vliegt met een snelheid van 15,0 m/s.
Hoe groot was de gemiddelde kracht die de knuppel
uitoefende op de bal?
A 200 N
B 400 N
C 600 N
D 1000 N
105
Botsende kogels
Een kogel P botst centraal tegen een kogel Q.
Op t = 0 s heeft kogel P een snelheid van 4,0 m/s
en kogel Q een snelheid van -2,0 m/s.
De snelheden voor, tijdens en na de botsing zijn in
het diagram weergegeven.
De massa van kogel P bedraagt 3,0 kg.
Hoe groot is de gemiddelde kracht die de kogel P tijdens de botsing ondervindt van kogel Q?
A 6,0 · 10² N
B 9,0 · 10² N
C 18 · 10² N
D 24 · 20² N
106
Op een trein die stil staat wordt door de motoren vanaf t = 0 een constante kracht uitgeoefend.
Tengevolge van deze kracht wordt de kinetische energie groter. De wrijving wordt
verwaarloosd.
In welk diagram is het verband tussen de kinetische energie en de tijd juist weergegeven?
Subdomein: Versnellen en vertragen
107
Welke van de volgende eenheden is te herleiden tot de eenheid van versnelling?
A N · kg
B N · kg-1
C N-1 · kg
D N-1 · kg-1
108
Bekijk de volgende beweringen:
1 Als een voorwerp in rust blijft, werken er geen krachten op dit voorwerp.
2 De versnelling van een voorwerp is recht evenredig met de resulterende kracht op dit
voorwerp.
Welke van deze beweringen is juist?
A zowel 1 als 2
B alleen 1
C alleen 2
D geen van beide
109
Een voorwerp ligt op de bodem van een lift die omhoog beweegt. De
snelheid van de lift verandert in de tijd zoals weergegeven wordt in het
(v,t)-diagram. De normaalkracht Fn op het voorwerp verandert in de tijd.
In welke figuur wordt het (Fn,t)-diagram het best weergegeven?
110
Een kracht F geeft aan een massa m1 een versnelling van 0,80 m/s². Deze kracht F geeft aan
een massa m2 een versnelling van 1,2 m/s².
Hoe groot is de versnelling die dezelfde kracht F geeft aan een massa m = m1 + m2?
A 0,40 m/s²
B 0,48 m/s²
C 1,0 m/s²
D 2,0 m/s²
111
Een kracht F van 30 N geeft een voorwerp met massa m1 een versnelling van 1,5 m/s².
Dezelfde kracht geeft aan een voorwerp met massa m2 een versnelling van 1,0 m/s².
Hoe groot is de versnelling die dezelfde kracht geeft aan een voorwerp met massa
m = m1 + m2?
A 0,50 m/s²
B 0,60 m/s²
C 1,25 m/s²
D 2,50 m/s²
112
Op een massa m1 werkt een kracht F van 2,4 N.
Massa m1 ondervindt een versnelling van 0,80 m/s². Als de kracht F op massa m2 werkt,
ondervindt deze een versnelling van 0,48 m/s².
Hoe groot is de versnelling die dezelfde kracht geeft aan een voorwerp met massa
m = m1 + m2?
A 1,28 m/s²
B 0,64 m/s²
C 0,32 m/s²
D 0,30 m/s²
113
Op een massa m1 werkt één kracht F. Massa m1 ondervindt een versnelling van 0,60 m/s².
Als de kracht F op een massa m2 werkt, ondervindt deze een versnelling van 0,40 m/s².
Hoe groot is de versnelling als kracht F op een massa m = m1 + m2 werkt?
A 1,0 m/s²
B 0,50 m/s²
C 0,24 m/s²
D 0,20 m/s²
114
Twee blokken met massa's 3,0 kg en 2,0 kg zijn op een
horizontaal vlak tegen elkaar geplaatst. Op het
linkerblok wordt horizontaal naar rechts een kracht van
4,0 N uitgeoefend, zoals in de figuur is aangegeven. De
blokken krijgen hierdoor een even grote, constante
versnelling.
Hoe groot is de kracht F die het linkerblok op het rechterblok uitoefent, als de
wrijvingskrachten worden verwaarloosd?
A F = 4,0 N
B F = 2,4 N
C F = 1,6 N
DF=0N
115
Twee blokken met massa's 2,0 kg en 3,0 kg zijn op een
horizontaal vlak tegen elkaar geplaatst. Op het linkerblok
wordt horizontaal naar rechts een kracht van 4,0 N
uitgeoefend, zoals in de figuur is aangegeven.
De blokken krijgen hierdoor een even grote, constante
versnelling.
Hoe groot is de kracht F die het linkerblok op het rechterblok uitoefent, als de
wrijvingskrachten worden verwaarloosd?
A 0,0 N
B 1,6 N
C 2,4 N
D 4,0 N
116
Op een horizontaal opgestelde luchtkussenbaan bevinden zich twee ijzeren sleetjes P en Q,
elk met een massa van 0,40 kg. Op sleetje P wordt een staafmagneet bevestigd, waarvan een
pool naar Q gericht is. De massa van de staafmagneet is 0,10 kg. De sleetjes worden op enige
afstand van elkaar losgelaten. De wrijving wordt verwaarloosd. Q krijgt een versnelling van
1,00 m/s².
Hoe groot is de versnelling die P krijgt?
A 1,25 m/s²
B 1,00 m/s²
C 0,80 m/s²
D 0,00 m/s²
117
Op een horizontaal opgestelde
luchtkussenbaan bevinden zich twee
ijzeren sleetjes P en Q, elk met een massa
van 0,20 kg. Op sleetje P wordt een
staafmagneet bevestigd, waarvan een pool naar Q gericht is. De massa van de staafmagneet is
0,10 kg. De sleetjes worden op enige afstand van elkaar losgelaten. De wrijving wordt
verwaarloosd. Q krijgt een versnelling van 0,6 m/s².
Hoe groot is de versnelling die P krijgt?
A 0,00 m/s²
B 0,40 m/s²
C 0,60 m/s²
D 0,90 m/s²
118
Op een horizontale tafel staat een karretje. Men oefent
hierop een horizontaal gerichte kracht F uit van 1,5 N.
De maximale wrijvingskracht op het karretje bedraagt
2,0 N.
Hoe groot is de resulterende kracht op het karretje?
A 0,0 N
B 0,5 N
C 1,5 N
D 3,5 N
119
Op een horizontaal vlak liggen twee blokken P en Q. Deze
zijn door koord 2 verbonden. De massa van P is 30 kg. De
massa van Q is 10 kg. Aan koord 1 trekt men P en Q over
een horizontaal vlak met een versnelling a = 0,20 m/s². De
wrijvingskrachten en de massa van de koorden worden verwaarloosd.
Hoe groot is de spankracht F1 in koord 1 en de spankracht F2 in koord 2?
A
B
C
D
F1
6,0 N
6,0 N
8,0 N
8,0 N
F2
2,0 N
6,0 N
2,0 N
8,0 N
120
Op een horizontale luchtkussenbaan bevindt zich
een sleetje met een massa van 0,40 kg. Dit sleetje
is met een koord, dat over een pen glijdt,
verbonden meteen blokje met een massa van
0,10 kg. De massa van het koord en de
wrijvingskrachten worden verwaarloosd.
Welke versnelling krijgen beide voorwerpen?
A 0,0 m/s²
B 2,0 m/s²
C 2,5 m/s²
D 9,8 m/s²
121
Voorwerp P, met een massa van 3,0 kg, bevindt zich op een
horizontaal tafelblad (zie tekening). Aan P is een koord
bevestigd dat over een pen kan glijden. Aan het andere
uiteinde van het koord hangt voorwerp Q met een massa van
2,0 kg. De massa van het koord en de wrijvingskrachten
worden verwaarloosd.
Hoe groot is de versnelling van de twee voorwerpen?
A 3,9 m/s²
B 5,9 m/s²
C 6,5 m/s²
D 9,8 m/s²
122
Twee voorwerpen P en Q zijn verbonden door een koord, dat over
een pen hangt. De massa van P is 0,6 kg, die van Q is 0,4 kg. De
massa van het koord en de wrijvingskrachten worden verwaarloosd.
De versnelling van de zwaartekracht is 10 m/s².
Welke van onderstaande formules geeft de juiste waarde van de
versnelling a van beide blokjes?
A (6 + 4) = (0,6 - 0,4)a
B (6 + 4) = (0,6 + 0,4)a
C (6 - 4) = (0,6 - 0,4)a
D (6 - 4) = (0,6 + 0,4)a
123
Op een ruw horizontaal vlak V ligt een voorwerp dat door een
kracht F in beweging wordt gebracht (zie figuur). F = 5,0 N.
De zwaartekracht Fz = 5,0 N, tan α = 0,75.
Hoe groot is de normaalkracht Fn?
A Fn = 8,0 N
B Fn = 5,0 N
C Fn = 3,0 N
D Fn = 2,0 N
124
Op een tafel ligt een voorwerp P. Op P werken (evenwijdig
aan het tafelblad) drie krachten van respectievelijk 3,0, 3,0 en
4,0 N (zie figuur). De maximale wrijvingskracht is 2,0 N.
Hoe groot is de resulterende kracht op P?
A 4,0 N
B 6,0 N
C 8,0 N
D 10,0 N
125
Op een tafel ligt een voorwerp P. Op P werken (evenwijdig
aan het tafelblad) drie krachten van respectievelijk 2,0, 3,0 en
4,0 N (zie figuur).
De maximale wrijvingskracht is 3,0 N.
Hoe groot is de resulterende kracht op P?
A 0,0 N
B 1,0 N
C 2,0 N
D 3,0 N
126
Op een tafel ligt een voorwerp P. Op P werken (evenwijdig
aan het tafelblad) drie krachten van respectievelijk 3,0, 3,0 en
4,0 N. Bovendien werkt op P een wrijvingskracht die
maximaal 3,0 N bedraagt.
Hoe groot is de resulterende kracht op P?
A 0,0 N
B 1,0 N
C 2,0 N
D 3,0 N
127
De relatie tussen de wrijvingskracht Fw, die een voorwerp ondervindt, en de snelheid v van het
voorwerp, is gegeven. Deze relatie is: Fw = C · v², waarin C een constante is.
Welke van de volgende eenheden is in het S.I. voor C een juiste eenheid?
A kg · m
B kg-1 · m
C kg · m-1
D kg-1 · m-1
128
In figuur 1 is het (v,t)-diagram van een
voorwerp P weergegeven. In figuur 2 is het
(v,t)-diagram van een voorwerp Q
weergegeven.
Wat weet je van de resulterende kracht FP
op voorwerp P en de resulterende kracht FQ
op voorwerp Q?
A
B
C
D
FP
FQ
is 0
is constant (≠ 0)
is 0
neemt af
is constant (≠ 0) is constant (≠ 0)
is constant (≠ 0)
neemt af
129
In figuur 1 is het (v,t)-diagram van een
voorwerp P weergegeven. In figuur 2 is het
(v,t)-diagram van een voorwerp Q
weergegeven.
Wat weet je van de resulterende kracht FP op
voorwerp P en de resulterende kracht FQ op
voorwerp Q?
FP
FQ
A
is 0
is constant (≠ 0)
B
is 0
neemt toe
C is constant (≠ 0) is constant (≠ 0)
D is constant (≠ 0)
neemt toe
130
De verplaatsing gedeeld door de tijdsduur waarin de verplaatsing plaatsvindt noemt men
A de snelheid.
B de gemiddelde snelheid in die tijdsduur.
C de afgelegde weg in die tijdsduur.
D de versnelling in die tijdsduur.
131
Een auto rijdt langs een rechte weg.
De snelheidsverandering gedeeld door de tijdsduur waarin de snelheidsverandering optreedt
noemt men
A de versnelling in die tijdsduur.
B de snelheid in die tijdsduur.
C de gemiddelde versnelling in die tijdsduur.
D de gemiddelde snelheid in die tijdsduur.
132
Bij een eenparig versnelde beweging verstaat men onder de versnelling
A de snelheidsverandering per seconde.
B de totale snelheidsverandering.
C de toename van de snelheid.
D de helft van de gemiddelde snelheid.
133
Gerda en Jaap spelen 'tikkertje'. Op een
zekertijdstip ziet Jaap Gerda op 20 m afstand
lopen. Haar snelheid is 7,0 m/s. Jaap kan met een
snelheid lopen van 9,0 m/s.
Jaap en Gerda lopen rechtdoor, zoals getekend.
Hoe groot is de hoek α tussen de baan van Gerda
en de baan van Jaap en na hoeveel seconde tikt
Jaap Gerda?
A
B
C
D
hoek
39
39
51
51
tijd
2,2 s
3,5 s
2,2 s
3,5 s
134
Twee sleetjes 1 en 2 met massa's m1 en m2, kunnen
wrijvingsloos op een luchtkussenbaan bewegen. Van beide
sleetjes bepaalt men de versnelling als ze met een bepaalde
kracht worden voortgetrokken. Men doet dit voor elk sleetje
bij vijf verschillende krachten en zet dan de versnelling uit
tegen de kracht (zie diagram).
Welke conclusie over m1 en m2 mag uit dit diagram worden getrokken?
A geen enkele, want er zijn geen getallen gegeven
B geen enkele, want er is niet met dezelfde krachten gewerkt
C m1 > m2, want de hellingshoek in het diagram die hoort bij slee 1 is groter
D m1 < m2, want slee 1 heeft voor dezelfde versnelling een kleinere kracht nodig
135
Een voorwerp met een massa van 0,50 kg wordt verticaal omhoog geworpen. De
wrijvingskracht met de lucht bedraagt op een bepaald moment tijdens de omhooggaande
verticale beweging 2,0 N.
Hoe groot is de vertraging op dat moment?
A 4,0 m/s²
B 5,8 m/s²
C 9,8 m/s²
D 13,8 m/s²
136
Op een voorwerp P van 3,0 kg werken slechts drie
krachten zoals in de figuur is weergegeven.
Hoe groot is de versnelling van P?
A 0,0 m/s²
B 2,0 m/s²
C 4,0 m/s²
D 6,0 m/s²
137
De plaatsfunctie van een bewegend punt P wordt gegeven door x = t + 2t2
Hoe groot is de gemiddelde snelheid van het punt P in de tijdsduur van t = 2 s tot t = 5 s?
A 7 m/s
B 9 m/s
C 15 m/s
D 45 m/s
138
Op het tijdstip t = 0 s begint een bal zonder beginsnelheid langs een hellend vlak naar beneden
te rollen. De plaats van de bal wordt vanaf t = 0 elke seconde aangegeven door een * (zie
figuur).
Hoe groot is de versnelling?
A 0,2 m/s²
B 0,4 m/s²
C 0,6 m/s²
D 1,2 m/s²
139
Iemand geeft een bal een trap, waardoor de bal langs een hellend vlak omhoog rolt.
De bal is 4,0 s later weer terug. Tijdens het rollen ondervindt de bal iedere seconde een
snelheidsverandering van 6,0 m/s. De wrijving wordt verwaarloosd.
Welke beginsnelheid had de bal?
A 4,0 m/s
B 6,0 m/s
C 12 m/s
D 24 m/s
140
Een auto rijdt met een snelheid van 40 m/s in de richting van een onbewaakte overweg.
Bij het zien van de rode knipperlichten remt de bestuurder af met een constante vertraging van
8,0 m/s² tot hij stil staat.
Hoe lang is de remweg?
A 40 m
B 60 m
C 80 m
D 100 m
141
Een kogel met een massa m wordt in een dikke boom geschoten.
Veronderstel dat de kracht F die de kogel in het hout ondervindt
constant is. De snelheid van de kogel vlak voor het binnendringen is v.
De weg die de kogel in het hout aflegt is s.
Welke van onderstaande relaties is juist?
A m · v = 2F · s
B m · v² = 2F · s
Cm·v=F·s
D m · v² = F · s
Subdomein: Cirkelbeweging
142
De versnelling bij een eenparige cirkelbeweging verandert
A steeds van richting en van grootte.
B steeds van richting, maar niet van grootte.
C steeds van grootte, maar niet van richting.
D noch van grootte, noch van richting.
143
Een punt beweegt eenparig langs een cirkelomtrek.
Welke uitspraak is juist?
De middelpuntzoekende versnelling
A is geen versnelling, want de beweging is eenparig.
B zorgt ervoor dat de snelheid groter wordt.
C is van het middelpunt af gericht.
D zorgt dat het punt op de cirkel blijft.
144
Op een horizontale draaischijf ligt een voorwerp P. De schijf maakt een
constant aantal omwentelingen per seconde in de aangegeven richting. P
blijft ten opzichte van de schijf in rust ('draait mee'). De wrijving met de
lucht wordt verwaarloosd.
Welke richting heeft de wrijvingskracht die P van de schijf ondervindt?
145
Op een horizontale draaischijf ligt een voorwerp P. De schijf maakt een
constant aantal omwentelingen per seconden in de aangegeven richting. P
blijft ten opzichte van de schijf in rust ('draait mee'). De wrijving met de
lucht wordt verwaarloosd.
Welke richting heeft de wrijvingskracht die P van de schijf ondervindt?
146
Op een draaiende schijf ligt een munt. Op de munt werkt een
wrijvingskracht.
Welke pijl geeft de richting van de wrijvingskracht weer?
A pijl 1
B pijl 2
C pijl 3
D pijl 4
147
In de figuur geven de stippen telkens de
plaats aan van een voorwerp dat van P via Q,
R en S naar T beweegt. De tijdsduur waarin
het voorwerp van de ene stip naar de
volgende stip beweegt is constant.
Op het voorwerp werkt in Q slechts één
kracht, namelijk FQ. In S werkt er op het
voorwerp ook slechts één kracht en wel FS.
Welke uitspraak over de richting van FQ en
FS is juist?
A FQ en FS staan loodrecht op elkaar.
B FQ is naar links gericht en FS naar rechts.
C FQ is naar rechts gericht en FS naar links.
D FQ en FS zijn beide naar links gericht.
148
Een stoeltje S is door een touw SQ aan een zweefmolen
verbonden. Deze draait om as PR.
S voert een eenparige cirkelbeweging uit.
Welke pijl geeft de richting van de
middelpuntzoekende versnelling aan?
A pijl 1
B pijl 2
C pijl 3
D pijl 4
149
Een voorwerp met massa m voert een eenparige cirkelbeweging uit. De straal van de
cirkelbaan is r. De grootte van de snelheid van het voorwerp is v en de grootte van de
resulterende kracht die op het voorwerp werkt is F.
Welke relatie tussen m, r, v en F is juist?
A F · r = m · v²
BFr=m·v
C F · r² = m · v²
D F · r² = m · v
150
Een voorwerp met massa m voert een eenparige cirkelbeweging uit. De straal van de
cirkelbaan is r. De grootte van de snelheid van het voorwerp is v en de grootte van de
resulterende kracht die op het voorwerp werkt is F.
Welke relatie tussen m, r, v en F is juist?
Am·v=F·r
B m · v = F · r²
C m · v² = F · r
D m · v² = F · r²
151
Een auto voert een eenparige cirkelbeweging uit. De massa van de auto is 800 kg en zijn
snelheid is 72 km/h. De middellijn van de cirkelbaan is 160 m.
Hoe groot is de middelpuntzoekende kracht die op de auto werkt?
A 2,0 kN
B 4,0 kN
C 26 kN
D 52 kN
152
Een auto voert een eenparige cirkelbeweging uit. De massa van de auto is 800 kg en zijn
snelheid is 72 km/h. De straal van de cirkelbaan is 80 m.
Hoe groot is de middelpuntzoekende kracht die op de auto werkt?
A 2,0 kN
B 4,0 kN
C 26 kN
D 52 kN
177
Twee coureurs nemen in identieke auto's naast elkaar een bocht, die een
kwart cirkel vormt. Ze doen even lang over de bocht. De stralen van de
cirkelbanen verhouden zich als 5 : 4. Bij het nemen van de bocht werkt
op de auto's een middelpuntzoekende ksracht van respectievelijk F1 en
F2.
Hoe groot is de verhouding F1 : F2?
A4:5
B5:4
C 16 : 25
D 25 : 16
178
Twee deeltjes P en Q voeren elk een eenparige cirkelbeweging uit. De massa's van P en Q zijn
even groot, evenals de middelpuntzoekende krachten (centripetale krachten) op P en Q. De
straal van de cirkelbaan van P is 4,0 m, die van Q is 1,0 m. De grootte van de snelheid van P
is 2,0 m/s.
Hoe groot is de snelheid van Q?
A 0,50 m/s
B 1,0 m/s
C 4,0 m/s
D 8,0 m/s