4.9 Lineaire benaderingen

4.9 Lineaire benaderingen
Versie 26 september
ü Inleiding
Er bestaat geen formule om alle functiewaarden van de sinus uit te rekenen. Voor
speciale hoeken kan de functiewaarde wel worden uitgerekend: sinH0L = 0,
sinJ N = , sinJ N =
p
6
1
2
p
4
1
2
2 etc. Een rekenmachine geeft de waarde 0.841471 voor
sinH1L. Dit is een goede benadering voor sinH1L. In de praktijk komt het vaak voor dat
men (functie)waarden niet exact kan bepalen. Men kan ze wel benaderen.
Beschouw een functie f met een punt a in het domein DH f L. Als men van f de
functiewaarde f HaL en de afgeleide f £ HaL kan berekenen, dan heeft men enig idee hoe
de grafiek van f rond het punt a loopt. Anders gezegd: men weet hoe f zich locaal
gedraagt rond a.
ü Idee
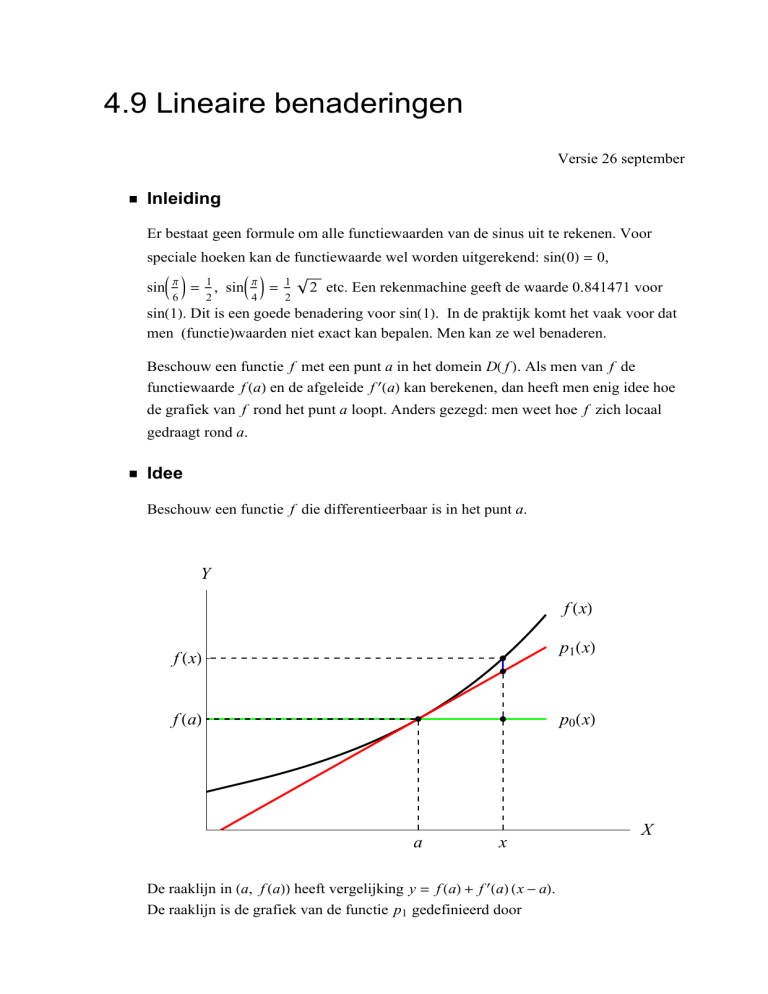
Beschouw een functie f die differentieerbaar is in het punt a.
Y
f HxL
p1 HxL
f HxL
f HaL
p0 HxL
a
x
De raaklijn in Ha, f HaLL heeft vergelijking y = f HaL + f £ HaL Hx - aL.
De raaklijn is de grafiek van de functie p1 gedefinieerd door
X
2
Section04_09.nb
p1 HxL = f HaL + f £ HaL Hx - aL.
De horizontale lijn door Ha, f HaLL is de grafiek van de functie p0 gedefinieerd door
p0 HxL = f HaL.
Als x º a, dan kan men f HxL door p1 HxL of p0 HxL benaderen. In het algemeen zal p1 HxL
een betere benadering zijn.
ü Lineaire benadering
Definitie
Beschouw een functie f die differentieerbaar is in het punt a.
Dan heet de functie p1 met p1 HxL = f HaL + f £ HaL Hx - aL de lineaire benadering
of de linearisatie van de functie f rond het punt a.
De functie p1 wordt ook met L aangegeven.
Laat de haakjes bij een lineaire benadering staan.
Als de lieaire benadering van een functie f rond het punt 1 gelijk is aan
p1 HxL = 2 - 3 Hx - 1L, dan moet f H1L = 2 en f £ H1L = -3. Natuurlijk is p1 HxL = 5 - 3 x,
maar f H1L en f £ H1L zijn nu niet gemakkelijk af te lezen.
ü Voorbeelden
Voorbeeld 1
Beschouw de functie f HxL =
x met afgeleide f £ HxL =
Rond a = 1 is de linearisatie LHxL = 1 +
1.1 = f H1.1L º LH1.1L = 1 +
1
2
Voorbeeld 2
Beschouw de functie f HxL =
1
x
1
4
1
10.2
1
4
Hx - 4L.
μ 0.1 = 2.025
met afgeleide f £ HxL = -
Rond a = 10 is de linearisatie LHxL =
Dan is
Hx - 1L.
= f H10.2L º LH10.2L =
1
10
x
μ 0.1 = 1.05
Rond a = 4 is de linearisatie LHxL = 2 +
4.1 = f H4.1L º LH4.1L = 2 +
1
2
1
2
1
10
-
1
100
-
1
100
Hx - 10L.
1
x2
μ 0.2 = 0.098
.
.
Section04_09.nb
3
Voorbeeld 3
Beschouw de functie f HxL = sinHxL.
Rond a = 0 is LHxL = x de linearisatie van f .
Nu is sinH0.1L = f H0.1L º LH0.1L = 0.1
We merken op dat sinH0.1L = 0.0998344, dus de benadering is niet slecht.
Voorbeeld 4
Neem f HxL =
Benader
36 + x . Dan
Deze is LHxL = 6 +
1
12
36 = 6, zal
37 = f H1L. We nemen de linearisatie van f rond a = 0.
37 met een linearisatie. Omdat
Hx - 1L. Dus
37 º LH1L = 6 +
Voorbeeld 5
De linearisatie van tanHxL rond a =
1
12
37 iets groter dan 6 zijn.
= 6.083
is p1 HxL = 1 + 2 Jx - N.
p
4
Een benadering voor tanI46° M = tanJ +
p
4
p
N
180
p
4
p
4
is LJ +
p
N
180
= 1+
p
90
ü Fout bij linearisatie
ü Stelling 11 Fout bij lineaisatie
Gegeven
functie f ,
interval I in DH f L met getallen a en x in I, x ∫ a,
f H2L is continu op I.
Dan geldt
(1) f HxL = f HaL + f £ HaL Hx - aL +
1
2
f ££ HsL Hx - aL2
voor een zeker punt s tussen a en x
De stelling zegt alleen dat er zo'n s bestaat en niet hoeveel het er zijn en hoe u ze kunt
vinden.
De term
1
2
f ££ HsL Hx - aL2 wordt de fout van de linearisatie genoemd en met E1 HxL
aangegeven.
Anders gezegd:
f HxL = p1 HxL + E1 HxL
4
Section04_09.nb
Zeker als x dicht bij a ligt, zal de fout klein zijn ten opzichte van Hx - aL.
Het teken van E1 HxL bepaalt of p1 HxL onder of boven f HxL ligt.
ü Voorbeelden
Voorbeeld 6
Geef benadering voor sinH0.1L met een geschikt interval er omheen.
Dan f HxL = sinHxL, a = 0 en LHxL = x.
Nu is x = 0.1 en sinH0.1L = LH0.1L + E1 H0.1L.
Nu is E1 H0.1L = - sinHsL H0.1L2 met 0 < s < 0.1.
1
2
Merk op dat 0 < sinHsL < sinH0.1L < 0.1.
Dus EH0.1L = -sinHsL ÿ 0.005 is negatief .
Er geldt dat -0.1 < -sinHsL < 0 ofwel -0.0005 < E1 H0.1L < 0.
Overal LH0.1L bij optellen levert 0.0995 < sinH0.1L < 0.1
De rekenmachine geeft sinH0.1L = 0.0998334.
Voorbeeld 7
Dan f HxL =
1.04 = f H1.04L, a = 1, f H1L HxL =
Geef benadering voor
x,
De linearisatie is LHxL = 1 +
x = 1.04; LH1.04L = 1 +
1
2
1
2
ÿ Hx - 1L.
1
2
Omdat 0 <
c
c
x
ÿ 0.04 = 1.02.
Er geldt f H1.04L = LH1.04L + E1 H1.04L en E1 H1.04L = 1
en f H2L HxL = -
1.04 met een geschikt interval er omheen.
1
< 1, vinden we -0.0002 < E1 H1.04L < 0.
Dus met optellen van LH1.04L vinden we 1.0198 <
8c
c
4x
x
.
H0.04L2 met 1 < c < 1.04.
1.04 < 1.02.
ü Opmerkingen
In LHxL haakjes van Hx - aL laten staan!
De linearisatie LHxL is een polynoom in x van de graad hoogstens 1.
Grafiek van linearisatie LHxL is rechte.
1