USolv-IT Toets

Formularium
Indienen
1.
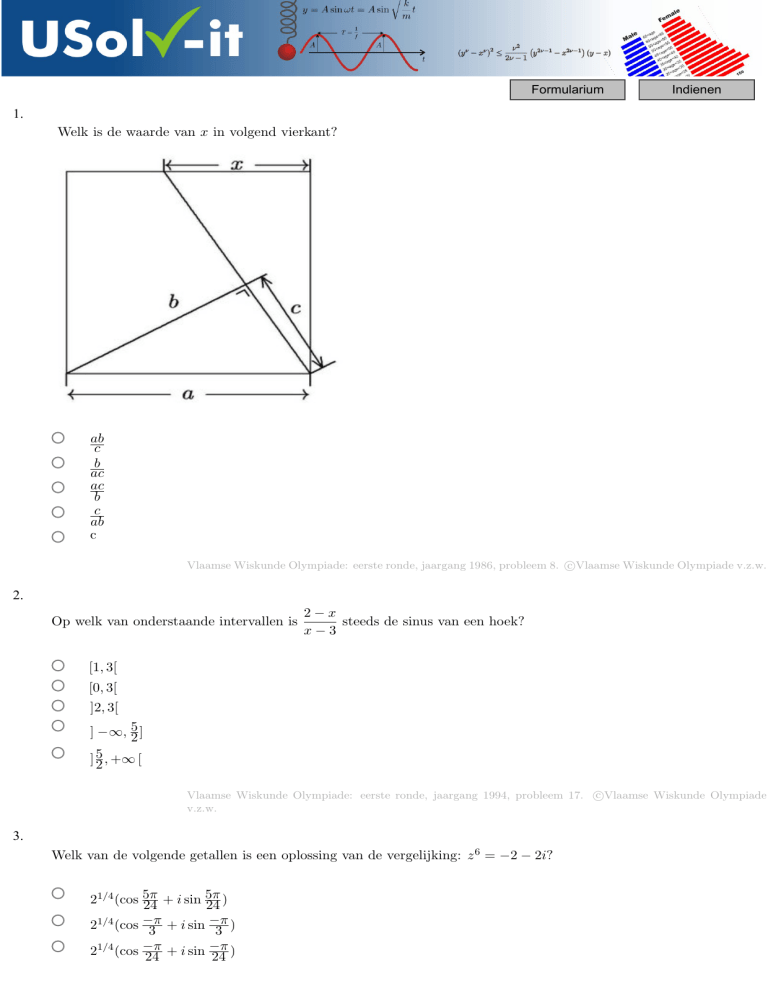
Welk is de waarde van x in volgend vierkant?
ab
c
b
ac
ac
b
c
ab
c
c
Vlaamse Wiskunde Olympiade: eerste ronde, jaargang 1986, probleem 8. Vlaamse
Wiskunde Olympiade v.z.w.
2.
Op welk van onderstaande intervallen is
2−x
steeds de sinus van een hoek?
x−3
[1, 3[
[0, 3[
]2, 3[
] −∞, 52 ]
] 25 , +∞ [
c
Vlaamse Wiskunde Olympiade: eerste ronde, jaargang 1994, probleem 17. Vlaamse
Wiskunde Olympiade
v.z.w.
3.
Welk van de volgende getallen is een oplossing van de vergelijking: z 6 = −2 − 2i?
5π
21/4 (cos 5π
24 + i sin 24 )
−π
21/4 (cos −π
3 + i sin 3 )
−π
21/4 (cos −π
24 + i sin 24 )
Info: auteur: Paul Igodt, Bram De Rock, id: 1014
4.
1 )) ?
Als f (x) = e3x−2 , wat is dan f (1 − ln( x
e
x3
ex3
e + x3
e + 13
x
Info: auteur: Tanja Costermans, Paul Igodt, bron: Oefenmateriaal 1ETEW - K.U.Leuven/KULAK, id: 1022
5.
In bijgaande figuur, opgebouwd met 2 congruente parallellogrammen is ~x + ~y gelijk aan
~a − 2~b
−2~b
3~a − 2~b
−~a − 2~b
−~a + 2~b
c
Vlaamse Wiskunde Olympiade: tweede ronde, jaargang 2001, probleem 14 Vlaamse
Wiskunde Olympiade
v.z.w
6.
Gegeven de functie
f (x) =


 x
als x < 1
x2
als 1 ≤ x ≤ 4
 √

8 x als x > 4
Welke van de volgende functies is de inverse van f ?
f1 (x) =


x
 √
als x < 1
x als 1 ≤ x ≤ 4


8x2 als x > 4


x
 √
als x < 1
x als 1 ≤ x ≤ 4
f2 (x) =
 x2

als x > 4
64


 x
√
als x < 1
x als 1 ≤ x ≤ 16
f3 (x) =
 x2

als x > 16
64


 x
√
als x < 1
x als 1 ≤ x ≤ 16
f4 (x) =
 x2

als x > 16
8
Info: inverse van een functie, auteur: Lutgarde Beernaert, bron: testnamiddag Analyse 1 nov 1996, id: 1558
7.
Welke uitspraak is juist ?
| x − 1| < 2
| x − 1| < 1
| x − 1| < 2
| x − 1| < 1
⇒
⇒
⇒
⇒
|f (x) − 0| < 1
|f (x) − 1| < 1
|f (x) − 2| < 2
|f (x) − 3| < 2
Info: auteur: Tanja Costermans, bron: oefenmateriaal 1ETEW - K.U.Leuven, id: 1596
8.
Beschouw de volgende functie:
f : R0 → R : x 7→
1−x x
e .
x
Dan geldt er:
f
f
f
f
heeft
heeft
heeft
heeft
geen extrema en geen buigpunten.
geen extrema maar wel een buigpunt.
wel een extremum maar geen buigpunten.
zowel een extremum als een buigpunt.
c
Info:
auteur: Wim Malfait, bron: Bavinck, ANALYSE, 250 tentamenopgaven met uitwerkingen, 1996, id:
1899
9.
Zij ~v , w
~ en ~u drie verschillende vectoren uit de euclidische vectorruimte R2 die voldoen aan
k~v k = kwk
~ = k~uk = 2
en
~v · w
~ =w
~ · ~u = 2.
Dan is
~v · ~u = 2.
~v · ~u = 4.
~v · ~u = −2.
~v · ~u uit de gegevens niet te bepalen.
c
Info:
Scalair product, auteur: Karel Dekimpe, Frederik Houpline, Kathleen Hoornaert, id: 2442
10.
Z
Bereken
1
2
1
2
1
2
1
2
t−
t+
t−
t−
sin2 t dt .
1
2
1
4
1
4
1
4
sin 2t + C
sin 2t + C
sin 2t + C
cos 2t + C , C ∈ R
Info: auteur: ann de bodt, tanja van hecke, id: 3804
11.
Voor welke van de volgende waarden

 2x
6x

2x
voor b1 , b2 , b3 is het onderstaande stelsel niet oplosbaar?
+ y + 7z = b1
− 2y + 11z = b2
− y + 3z = b3
(b1 , b2 , b3 ) = (1, 2, 3).
(b1 , b2 , b3 ) = (0, 5, 83 ).
(b1 , b2 , b3 ) = (5, 20, 7).
(b1 , b2 , b3 ) = (−1, 4, 0).
37
(b1 , b2 , b3 ) = ( 83 , 52 , 40
).
c
Info:
auteur: bron: Linear Algebra, Jin Ho Kwak and Sungpyo Hong, id: 6673
12.
Met de poolcoördinaten van een punt bedoelt men een afstand r en een hoek θ. Hierbij is
r de afstand van het punt tot de oorsprong van het assenstelsel.
θ is de hoek tussen de positieve X-as en de halve rechte die de oorsprong met het punt
verbindt. De hoek wordt gemeten in tegenwijzerzin.
Er bestaat het volgende verband tussen x, y enerzijds, en r, θ anderzijds:
x = r cos θ
y = r sin θ
Bij de vergelijking van een kromme in poolcoördinaten drukt men de afstand r van een punt
van de kromme tot de oorsprong uit als functie van de hoek θ. Welke van de onderstaande
figuren geeft de grafische voorstelling van
r = 2(1 − cos θ)
Info: Kromme poolcoord., auteur: Riet Callens, bron: Zomercursus, id: 7229
13.
Twee heel dunne staven zijn scharnierend verbonden in het punt A en vormen een hoek θ.
Tussen deze staven wordt een schijfje geklemd met straal R en centrum O. De afstand a = |OA|
tussen het centrum van het schijfje O en het scharnierpunt A van de staven hangt af van de
hoek θ zodat we de functie f kunnen definiëren met a = f (θ) . Wat is de afgeleide van deze
functie f voor θ = 2π/3?
−4R/3
−R/3
√
−R/ 3
Geen van voorgaande.
Info: goniometrie, auteur: Riet Callens, bron: Zomercursus, id: 7230
14.
Zij f : [0, 1] → R een integreerbare functie (niet noodzakelijk continu). Stel I =
Dan geldt:
Als I
Als I
Als I
Geen
≥ 0, dan is f (x) ≥ 0 voor alle x ∈ [0, 1].
= 0, dan bestaat er een x ∈ [0, 1] waarvoor f (x) = 0.
6= 0, dan is f (x) 6= 0 voor alle x ∈ [0, 1].
van vorige.
Z 1
f (t) dt.
0
Info: integralen, auteur: Johan Quaegebeur, Frederik Houpline, Tine Beernaert, Kaat Zeeuwts, bron: sept99,
Zomercursus, id: 7231
15.
Bepaal de vergelijking van het vlak door het punt (1, 0, 0) en dat de rechte met vergelijking
y +2z = 1
3x +4y +5z = 1
omvat.
x+y+z =1
x + 2y + 3z = 1
3x + 4y + 5z = 3
Geen van vorige vergelijkingen.
Info: Rechten vlakken, auteur: Jeroen Dehaene, bron: Zomercursus, id: 7232
16.
De k-de afgeleide (k ∈ N) van een reële functie f met één reële veranderlijke wordt bekomen
door de functie k maal af te leiden (k 6= 0), de 0-de afgeleide van de functie definiëren we als
f (0) = f .
k! is de faculteit van het natuurlijk getal k en heeft als definitie k! = 1 · 2 ··· (k − 1) · k voor
k 6= 0 en 0! = 1.
1 waarbij
De formule voor de k-de afgeleide van de reële functie f met voorschrift f (x) = 1 −
x
x ∈ R en x 6= 1 wordt gegeven door
f (k) (x) =
(−1)k k!
(1 − x)2k
f (k) (x) =
k!
(1 − x)k+1
f (k) (x) =
k!
(1 − x)k−1
(−1)k
k! (1 − x)k+1
geen van vorige.
f (k) (x) =
Info: k-de afgeleide, auteur: kaat zeeuwts, bron: Zomercursus, id: 7233
17.
Bepaal de som van de elementen van de laatste kolom van de inverse van
Ö
0 1 1
2 4 2
1 2 2
1
−2
3
Geen van voorgaande oplossingen.
è
.
Info: Inverse, auteur: Jeroen Dehaene, bron: Zomercursus, id: 7234
18.
Voor elke n ∈ N0 en elke x ∈ R0 is
n
X
nk xk−1 gelijk aan
k=1
n−1
X
(n − 1)k xk−1 .
k=0
n−1
X
nk+1 xk .
k=0
n−1
X
nk−1 xk−2 .
k=0
geen van vorige.
Info: sommatie(substitutie), auteur: Kaat Zeeuwts, bron: Zomercursus, id: 7235
19.
In onderstaande figuur zijn de grafieken van een functie f geschetst, haar eerste afgeleide f 0 en
haar tweede afgeleide f 00 . Welke kromme correspondeert met de grafiek van f , welke met die
van f 0 ?
De grafiek van f is een streepjeslijn, die van haar afgeleide f 0 is een volle lijn.
De grafiek van f is een streepjeslijn, die van haar afgeleide f 0 is een stippellijn.
De grafiek van f is een volle lijn, die van haar afgeleide f 0 is een stippellijn.
De grafiek van f is een stippellijn, die van haar afgeleide f 0 is een volle lijn.
Indienen
Info: Functieverloop van een functie m.b.v de eerste en de tweede afgeleide, auteur: Kathleen Hoornaert, Kaat
Zeeuwts, id: 7236
20.
Duid in volgende reeks alle alternatieven aan waarbij Uitspraak (1) precies dezelfde
betekenis heeft als Uitspraak (2).
(1)
(2)
(1)
(2)
(1)
(2)
(1)
(2)
(1)
(2)
Niet alle jongeren sporten en fuiven graag.
Er zijn jongeren die niet graag sporten en niet graag fuiven.
Niet alle domme jongeren zijn blonde meisjes.
Er bestaan domme meisjes die niet blond zijn.
Het is niet zo dat sommige mensen ongezond eten.
Sommige mensen eten niet ongezond.
Alle kinderen die niet goed zijn in wiskunde, zijn jongens.
Alle meisjes zijn goed in wiskunde.
Alle kinderen die goed zijn in wiskunde zijn meisjes.
Alle meisjes zijn goed in wiskunde.
Info: Logica neg contrapositie, auteur: Kaat Zeeuwts, bron: Zomercursus, id: 7237