Samenvattingen vwo b die niet in einddeel

JOBNAME: 9001.60655.5.MW9.vwo PAGE: 19 SESS: 31 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/104⫺4⫺
Hoofdstuk 4
Samenvatting
Machtsfunctie
De functie f共x兲 ⫽ x n heet een machtsfunctie. Het verloop van de grafiek
hangt af van de waarde van n.
Gebroken functie
Machtsfuncties waarbij n een negatief geheel getal is heten gebroken
functies.
Wortelfuncties
Machtsfuncties waarbij n een breuk is heten wortelfuncties.
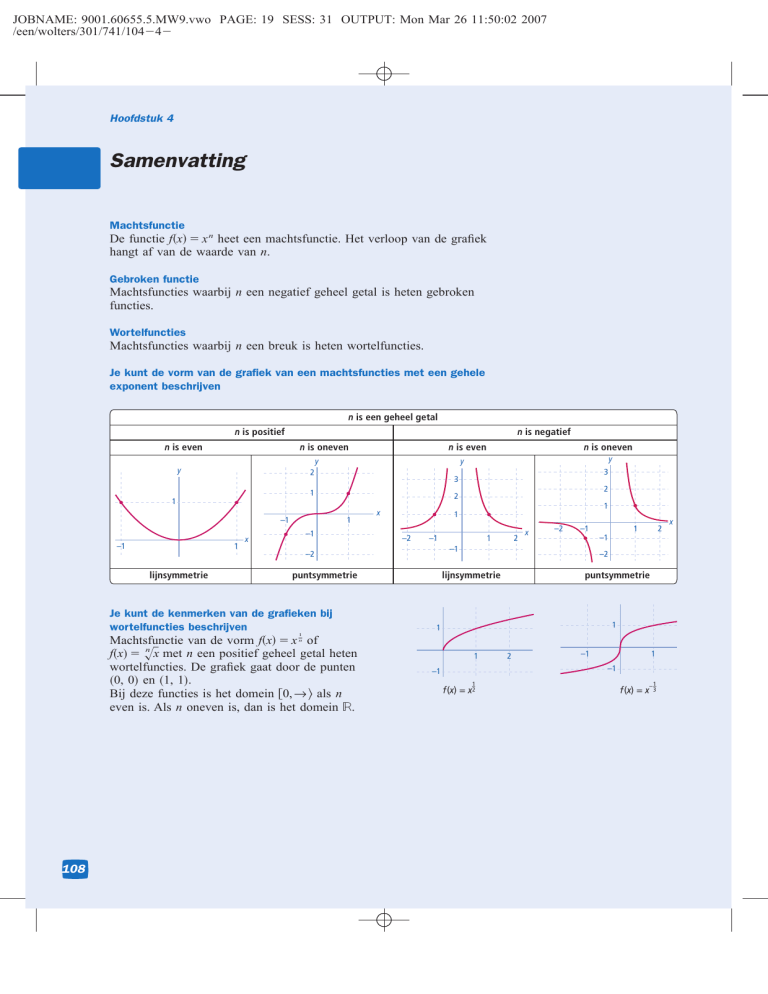
Je kunt de vorm van de grafiek van een machtsfuncties met een gehele
exponent beschrijven
n is een geheel getal
n is positief
n is even
n is negatief
n is oneven
n is even
y
y
2
–1
1
1
–1
1
x
1
–2
–1
puntsymmetrie
Je kunt de kenmerken van de grafieken bij
wortelfuncties beschrijven
Machtsfunctie van de vorm f共x兲 ⫽ x of
n
f共x兲 ⫽ 冪
x met n een positief geheel getal heten
wortelfuncties. De grafiek gaat door de punten
共0, 0兲 en 共1, 1兲.
Bij deze functies is het domein 关0, → 典 als n
even is. Als n oneven is, dan is het domein R.
1
2
x
–2
–1
1
2
–1
–1
–2
lijnsymmetrie
2
2
1
x
y
3
3
1
–1
n is oneven
y
–2
lijnsymmetrie
puntsymmetrie
1
1
1
n
108
1
2
–1
1
–1
–1
1
f(x) = x–2
1
f(x) = x– –3
x
JOBNAME: 9001.60655.5.MW9.vwo PAGE: 20 SESS: 31 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/104⫺4⫺
Hoofdstuk 4
Je kunt machtsfuncties met een negatieve exponent schrijven
als een gebroken functie
Er geldt f共x兲 ⫽ x ⫺n ⫽ 1n
x
Voorbeeld
Schrijf de functies f(x) = x–3 en
g(x) = x–8 zonder negatieve exponenten.
Oplossing
1
1
f(x) = ––
3 en g(x) = ––
8
x
x
Voorbeeld
Je kunt de vergelijking x n ⫽ c exact oplossen
De vergelijking x ⫽ c heeft 0, 1 of 2
oplossingen. Bepaal eerst, eventueel met een
plot, het aantal oplossingen.
Eén oplossing is x ⫽ c .
Als er twee oplossingen zijn dan is de andere
oplossing x ⫽ ⫺c .
Los exact op x4 = 3.
Je kunt vergelijkingen met twee machtsfuncties exact
oplossen
Voorbeeld
n
Oplossing
In een plot zie je dat er twee oplossingen zijn.
1
4
De ene oplossing is x = 3–4 = √3.
4
De andere oplossing is x = –√3.
1
n
1
n
Herleid de vergelijking op 0 en ontbind in factoren.
Uit de vorm A ⭈ B ⫽ 0 volgt A ⫽ 0 of B ⫽ 0.
Los exact op 9x2 = 3x6.
Oplossing
9x2 = 3x6
9x2 – 3x6 = 0
3x2(3 – x4) = 0
3x2 = 0 of x4 = 3
4
4
x = 0 of x = √3 of x = –√3
Je kunt het gedrag verklaren van functies die uit twee
machtsfuncties zijn samengesteld
Bekijk het gedrag voor heel grote waarden van x en voor
waarden van x dicht bij 0.
Voorbeeld
1
Omschrijf het gedrag van de functie f(x) = x2 – ––
4
y
x
Oplossing
1
Voor grote waarden van x wordt ––
4 een klein getal. De grafiek van f ligt dan dicht
f
4
x
bij de grafiek van g(x) = x2. Als je voor x een getal dicht bij 0 invult dan wordt x2
1
een klein getal. De grafiek van f lijkt op de grafiek van h(x) = – ––
4
x
g
6
2
g
–3 h –2
–1
1
2
h3
x
–2
–4
–6
f
109
JOBNAME: 9001.60655.5.MW9.vwo PAGE: 21 SESS: 36 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/104⫺4⫺
Hoofdstuk 4
Test jezelf
Op de computer vind je ook een Test jezelf met andere opdrachten.
T-1
a
b
c
Gegeven zijn de functies f共x兲 ⫽ x 4 en g共x兲 ⫽ x 7.
Welke symmetrie-eigenschappen hebben de grafieken van deze functies?
Onderzoek of de functie h共x兲 ⫽ f共x兲 ⫹ g共x兲 te schrijven is als een
machtsfunctie h共x兲 ⫽ x n. Zo ja welke exponent hoort er dan bij?
Beantwoord dezelfde vragen voor de functie k共x兲 ⫽ f共x兲 ⭈ g共x兲.
Deze opdracht hoort bij paragraaf 4-1.
T-2
a
b
c
Gegeven is de functie f共x兲 ⫽ 2 ⫹ x ⫺4.
Plot de grafiek van f en los exact op: f共x兲 ⫽ 4.
Los op: f共x兲 ⬎ 100.
Leg uit hoe je aan het functievoorschrift kunt zien dat de
grafiek van f de x-as niet snijdt.
Deze opdracht hoort bij paragraaf 4-2.
T-3
In Noord-Amerika is een verband geconstateerd tussen de oppervlakte van
een leefgebied en het aantal verschillende vogelsoorten dat er voorkomt.
De formule die het verband weergeeft is S ⫽ 40 ⭈ A .
S is het aantal vogelsoorten en A is de oppervlakte van het leefgebied in
vierkante mijl.
Bereken het aantal vogelsoorten in gebieden met een oppervlakte van
0,75 vierkante mijl en een oppervlakte van 1500 vierkante mijl.
In een gebied in Noord-Amerika komen zo’n 50 vogelsoorten voor.
Bereken de oppervlakte van dat gebied.
De oppervlakte van een gebied wordt tien keer zo groot genomen. Wordt
het aantal vogelsoorten ook tien keer zo groot? Verklaar je antwoord met
een berekening.
Een klein gebied en een groot gebied worden beide met 50 vierkante mijl
uitgebreid. Leg uit in welke van deze twee gevallen het aantal vogelsoorten
het meest zal toenemen.
Druk A uit in S.
De oppervlakte O in km 2 is te berekenen met de formule O ⫽ 2,56 ⭈ A.
Daaruit volgt dat S ⫽ c ⭈ O Bereken c.
Deze opdracht hoort bij paragraaf 4-3.
1
6
a
b
c
d
e
f
1
6
110
JOBNAME: 9001.60655.5.MW9.vwo PAGE: 22 SESS: 38 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/104⫺4⫺
Hoofdstuk 4
T-4
a
b
c
d
Los exact op.
x 3 ⫽ ⫺12
3x 2 ⫹ 2x 5 ⫽ 0
x ⫽ 23
x ⫺ ⫽ 23
Deze opdracht hoort bij paragraaf 4-4.
T-5
Gegeven is de functie f共x兲 ⫽ x 2 ⫹ 1
x
Bereken exact de coördinaten van het
nulpunt van f.
Voor grote waarden van x lijkt de grafiek van
f op de parabool met vergelijking y ⫽ x 2.
Leg met het functievoorschrift van f uit hoe
dat komt.
In de buurt van x ⫽ 0 lijkt de grafiek van f
op de grafiek van y ⫽ 1
x
Leg uit hoe dat komt.
Deze opdracht hoort bij paragraaf 4-5.
a
b
c
T-6
a
b
c
T-7a
b
T-8
a
b
c
T-9
x 5 ⫽ ⫺7x 3
x 3 ⱕ 2x 4
x ⫺ ⬎ ⫺ 12
4
冪x ⬍ 12
e
f
g
h
1
4
1
4
1
3
y
8
6
4
2
–4
–3
–2
–1
O
1
2
3
4
x
Gegeven is de functie f共x兲 ⫽ 2 ⫹ 2500 ⭈ x ⫺1 met x ⬎ 0.
Wat gebeurt er met de functiewaarden als de waarde van x toeneemt?
Alle functiewaarden van f liggen boven een bepaalde waarde. Beredeneer
met het functievoorschrift welke waarde dat is.
Los exact op: 4 ⱕ f共x兲 ⱕ 6.
Geef een voorbeeld van een machtsfunctie met domein 关0, → 典.
Geef een voorbeeld van een machtsfunctie met domein 具 ← , 0典.
Gegeven zijn de functies f共x兲 ⫽ x 2 en g共x兲 ⫽ 共x ⫺ 3兲 2.
Los exact op f共x兲 ⫽ 10.
Hoe kun je de oplossingen van g共x兲 ⫽ 10 hieruit afleiden?
Gegeven is de functie h共x兲 ⫽ 共x ⫹ a兲 2 met h共3兲 ⫽ 25.
Bereken de exacte waarde van h共4兲
Los exact op: g共x兲 ⫽ h共x兲.
Van de functies f共x兲 ⫽ x a ⫹ x b is gegeven dat de grafiek de x-as niet snijdt.
Wat weet je van de getallen a en b?
111
JOBNAME: 9001.60655.5.MW9.vwo PAGE: 21 SESS: 106 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/105⫺4⫺
Hoofdstuk 5
Samenvatting
Definitie
Met een definitie leg je een begrip vast. Daarvoor gebruik je
uitsluitend reeds bekende begrippen.
Stelling
Een stelling is een bewezen bewering of eigenschap. Je mag
bewezen stellingen gebruiken bij een volgend bewijs.
∠ A = 2 · ∠C
∠B = 30°
∠ A + ∠B + ∠C = 180°
⇒ ∠C = 50°
Implicatie en implicatieteken
Als je uit een aantal gegevens een conclusie trekt kun je dit
weergeven met het implicatieteken. Daarbij staan de gegevens
links van een accolade en het implicatieteken.
Dus: gegevens of definities ⇒ nieuwe eigenschap
Equivalent en equivalentieteken
Eigenschappen of definities zijn equivalent 共⫽ gelijkwaardig兲
als je uitgaande van de ene de andere kunt bewijzen en
omgekeerd. Dus: oude eigenschap of definitie ⇔ nieuwe
eigenschap of definitie
Bewijzen
Om een bewijs van een eigenschap of een stelling te vinden
moet je meestal de hiernaast genoemde stappen doorlopen.
Bij het uitschrijven van een bewijs volg je het bewijsschema
hiernaast.
Bewijs aanpak
1 Verkennen
2 Analyseren
• Vooruitdenken
• Terugdenken
• Plan maken
3 Bewijs geven
Gelijkvormigheid
Twee figuren zijn gelijkvormig als de ene figuur een
vergroting of een verkleining van de andere is.
Dan zijn overeenkomstige hoeken gelijk en is er een vaste
verhouding tussen de overeenkomstige zijden.
Bewijsschema
1 Gegeven
2 Te bewijzen
3 Bewijs
Congruentie
Twee driehoeken zijn congruent als overeenkomstige hoeken
en overeenkomstige zijden gelijk zijn.
Indirect bewijs
Een bewijs van een stelling kun je soms indirect geven door
gebruik te maken van gevalsonderscheiding. Je bewijst dan
dat alle mogelijkheden op één na tot een tegenspraak leiden.
Bij een bewijs uit het ongerijmde laat je zien dat het geval
onwaar tot een tegenspraak leidt. En dus blijft alleen het
geval waar over.
De onjuistheid van een bewering toon je aan door het geven
van tenminste één tegenvoorbeeld.
148
Voorbeeld
Bewijs dat een driehoek hoogstens één
stompe hoek heeft.
Oplossing
Stel dat in driehoek ABC de hoeken bij A en bij B
stomp zijn. Dan geldt:
∠A + ∠B + ∠C > 180°
Dit is in tegenspraak met de stelling van de
hoekensom.
JOBNAME: 9001.60655.5.MW9.vwo PAGE: 22 SESS: 107 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/105⫺4⫺
Hoofdstuk 5
Je kunt vaststellen of twee driehoeken gelijkvormig of
congruent zijn
De meest gebruikte gelijkvormigheidskenmerken voor twee
driehoeken zijn:
> alle overeenkomstige zijden hebben dezelfde verhouding
of
> twee paar overeenkomstige hoeken zijn gelijk.
Twee driehoeken zijn congruent als ze voldoen aan één van
de vijf congruentiegevallen ZZZ, ZHZ, HZH, ZHH of ZZR.
Voorbeeld
Gegeven: driehoek ABC is gelijkbenig,
∠Q = 90° en ∠R = 90°.
Bewijs dat PBQ ⵒ PAR.
Oplossing
∠Q = ∠R (= 90°)
∠B = ∠BAC = ∠PAR
PBQ ⵒ
C
Q
PAR
P
A
B
R
Je kunt bewijzen dat twee definities equivalent zijn
Je moet dan uitgaande van de ene definitie de andere definitie als
eigenschap bewijzen én uitgaande van de andere definitie de ene als
eigenschap bewijzen.
gelijkzijdige driehoek
gelijkzijdige driehoek
Een gelijkzijdige driehoek is een driehoek waarvan alle zijden
Een gelijkzijdige driehoek is een driehoek waarvan alle hoeken
even lang zijn.
gelijk zijn.
Voorbeeld
A
Bewijs de equivalentie van de definities hierboven.
Oplossing
Bewijs ⇒
Gegeven: ABC met |AB| = |AC| = |BC|
Te bewijzen: Alle hoeken zijn gelijk.
Bewijs: |AC| = |BC| ⇒ ∠A = ∠B
Op dezelfde manier: |AB| = |AC| ⇒ ∠B = ∠C
Dus alle hoeken zijn gelijk.
Bewijs ⇐
Gegeven: ABC met ∠A = ∠B = ∠C
Te bewijzen: Alle zijden zijn even lang.
Bewijs: ∠A = ∠B ⇒ |BC| = |AC|
∠B = ∠C ⇒ |AC| = |AB|
Dus alle zijden zijn even lang.
B
C
149
JOBNAME: 9001.60655.5.MW9.vwo PAGE: 23 SESS: 118 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/105⫺4⫺
Hoofdstuk 5
Test jezelf
Op de computer vind je ook een Test jezelf met andere opdrachten.
T-1
a
b
C
Gegeven is een scherphoekige driehoek ABC met daarin de
hoogtelijnen AD en BE.
Deze hoogtelijnen snijden elkaar in punt H.
Bewijs dat de driehoeken AHE en BHD gelijkvormig zijn.
|AD| |BE|
⫽
.
Bewijs dat
|AC| |BC|
Deze opdracht hoort bij paragraaf 5-1.
D
E
H
A
T-2
B
m
In driehoek ABC is lijn m de middelloodlijn van AB.
Lijn m snijdt AC in D.
De bissectrice van ⬔C snijdt de lijn m in punt S.
Bewijs dat ⬔DSC ⫽ ⬔B ⫹ 12 ⬔C ⫺ 90⬚.
Deze opdracht hoort bij paragraaf 5-2.
C
D
B
A
T-3
a
b
c
T-4
a
b
c
d
150
Van driehoek ABC is gegeven dat |AB| ⫽ 4, ⬔A ⫽ 35⬚ en ⬔C ⫽ 80⬚.
Teken een driehoek die aan de gegevens voldoet.
Didy en Marijke tekenen elk een driehoek volgens de gegevens.
Zijn hun driehoeken congruent?
Zo ja, op grond van welk congruentiegeval?
Zo nee, teken een andere driehoek die ook aan de gegevens voldoet.
Beantwoord dezelfde vragen voor driehoek DEF met |DE| ⫽ 4,
|EF| ⫽ 5 en ⬔F ⫽ 40⬚.
Deze opdracht hoort bij paragraaf 5-3.
In de figuur hiernaast snijden de benen van ⬔A
en ⬔B elkaar in de punten C, F, G en H.
Gegeven is dat ⬔A ⫽ ⬔B.
Te bewijzen: ⬔ECF ⫽ ⬔DGF
Zie je direct een bewijs, geef dat dan.
Analyseren: vooruitdenken
Je weet niets over afstanden. Dus congruentie?
Gegeven is ⬔A ⫽ ⬔B
In welke stellingen komen gelijke hoeken voor?
Analyseren: terugdenken
Welke hoek is gelijk aan ⬔ECF?
En welke hoek is gelijk aan ⬔DGF?
Maak een plan en geef het bewijs.
Deze opdracht hoort bij paragraaf 5-4.
S
E
D
F
C
G
H
A
B
JOBNAME: 9001.60655.5.MW9.vwo PAGE: 24 SESS: 113 OUTPUT: Mon Mar 26 11:50:02 2007
/een/wolters/301/741/105⫺4⫺
Hoofdstuk 5
T-5
Toon aan dat de onderstaande definities van een rechthoek equivalent zijn.
rechthoek
rechthoek
rechthoek
Een vierhoek met vier rechte
hoeken is een rechthoek.
Een parallellogram met een
rechte hoek is een rechthoek.
Een paralllellogram met
gelijke diagonalen is een rechthoek.
Deze opdracht hoort bij paragraaf 5-5.
T-6
a
b
T-7a
b
c
d
T-8
a
b
c
d
e
T-9
a
b
In de figuur worden de lijnen l en m gesneden door een derde
lijn. Als Z-hoeken gelijk zijn dan zijn l en m twee
evenwijdige lijnen. Waarschijnlijk heb je dit zonder bewijs
geaccepteerd. Maar je kunt het ook bewijzen!
Geef een definitie van twee evenwijdige lijnen.
Bewijs dat als Z-hoeken gelijk zijn dat dan l en m evenwijdig
zijn. Geef een bewijs uit het ongerijmde.
Deze opdracht hoort bij paragraaf 5-6.
l
m
Q
Voer de volgende constructie uit met GeoGebra.
1 Teken twee punten M en P en teken de cirkel c 1 met
middelpunt M en straal |MP|.
2 Neem punt Q op de cirkel en teken de lijnstukken MP,
MQ en PQ.
3 Neem een punt N op lijnstuk MP en teken cirkel c 2 met
middelpunt N en |NP| als straal. Deze cirkel snijdt PQ in K.
4 Teken de lijn l door K evenwijdig aan MP. Lijn l snijdt
MQ in L.
Welk soort vierhoek is vierhoek KLMN?
Controleer door hoeken of lengten te meten.
Versleep punt N langs MP. Blijf je dezelfde vierhoek zien?
Bewijs je vermoeden omtrent vierhoek KLMN.
Deze opdracht hoort bij paragraaf 5-7.
Gegeven is een parallellogram ABCD. Punt P is het midden
van zijde AB en punt Q is het midden van zijde CD.
Bewijs dat APCQ een parallellogram is. Maak hierbij gebruik
van congruente driehoeken en van één van de definities van
een parallellogram.
Bewijs dat vierhoek PBCQ een parallellogram is.
Bewijs dat vierhoek PBRS een parallellogram is.
Bewijs dat vierhoek PRQS een parallellogram is.
Bewijs: Als vierhoek PRQS een ruit is, dan is ABCD een
rechthoek.
K
L
l
P
N
M
c2
c1
D
Q
S
A
C
R
P
B
Als je de middens van de zijden van een willekeurige
vierhoek ABCD verbindt krijgt je vierhoek PQRS.
Wat kun je zeggen van ABCD als PQRS een ruit is?
En als PQRS een rechthoek is?
151
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 21 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/102⫺4⫺
Hoofdstuk 2
Samenvatting
Transformatie
Een transformatie is bijvoorbeeld een verschuiving 共translatie兲, spiegeling
of vermenigvuldiging van een grafiek, of een combinatie hiervan. Door een
transformatie van een grafiek verandert het functievoorschrift.
Verschuiven
Als de grafiek van een functie f over een afstand d omhoog wordt
verschoven heeft het functievoorschrift van de nieuwe grafiek de vorm
g共x兲 ⫽ f共x兲 ⫹ c.
Als de grafiek van een functie f naar over een afstand c naar rechts wordt
verschoven is het functievoorschrift van de nieuwe grafiek g共x兲 ⫽ f共x ⫺ c兲.
Vermenigvuldigen
Als je bij een grafiek de afstand van elk punt tot de x-as a keer zo groot
maakt wordt het nieuwe functievoorschrift g共x兲 ⫽ a ⭈ f共x兲.
Als je bij een grafiek de afstand van elk punt tot de y-as b keer zo klein
maakt vervang je in een functievoorschrift de x door bx.
Als a of b negatief is komen de punten bovendien aan de andere kant van
respectievelijk de x-as of de y-as te liggen.
Standaardgrafieken
De grafieken van de functies hiernaast heten standaardgrafieken.
Van deze grafieken moet je de kenmerken kennen.
Standaardfuncties
f(x) = x, g(x) = x2, h(x) = x3,
1
k(x) = √x, n(x) = –,
x p(x) = 1,
s(x) = sin x, c(x) = cos x,
m(x) = 2x en l(x) = 2logx
Parameter
Een familie van functies beschrijf je handig door gebruik te
maken van een hulpvariabele of parameter.
Je kunt het functievoorschrift aanpassen na een vermenigvuldiging
of translatie
Voorbeeld
y
Gegeven is de functie f(x) = 0,5x 2 – 2x
Wat zijn de functievoorschriften van de beeldgrafiek als de
grafiek van f een afstand 1 omhoog en 3 naar links wordt verschoven?
4
3
2
Oplossing
Als de grafiek 3 naar links schuift, vervang je de x door x + 3.
Als de grafiek 1 omhoog schuift, moet je bij het functievoorschrift
1 optellen. Het nieuwe functievoorschrift wordt dus:
g(x) = 0,5(x + 3)2 – 2(x + 3) + 1.
1
–5
–4
–3
–2
–1 O
–1
–2
–3
52
1
2
3
4
5
x
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 22 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/102⫺4⫺
Hoofdstuk 2
Voorbeeld
1
–3
1
Gegeven zijn de functies f(x) = –,
x g(x) = ––
x en h(x) = ––
3x
Hoe zijn de grafieken van g en h ontstaan uit de grafiek van f?
Oplossing
Omdat g(x) = –3 . f(x) is de afstand van elk punt op de grafiek
van g vermenigvuldigd met 3 ten opzichte van de x-as. Door
het min-teken is er bovendien gespiegeld in de x-as.
Omdat h(x) = f(3x) is de afstand van elk punt op de grafiek van
f vermenigvuldigd met –1 ten opzichte van de y-as.
3
Je kunt het functievoorschrift opstellen bij een grafiek die uit een
standaardgrafiek is ontstaan
1 Kijk welke standaardgrafiek in aanmerking komt.
2 Let op randpunten, asymptoten en toppen om te ontdekken welke
translaties ten opzichte van de standaardgrafiek hebben plaatsgevonden
3 Stel vast of de standaardgrafiek horizontaal of verticaal moet worden
vermenigvuldigd om de gegeven grafiek te krijgen.
4 Stel het functievoorschrift op en controleer het met een plot.
Voorbeeld
De grafiek van f hiernaast is ontstaan uit een standaardgrafiek.
Wat is het voorschrift van de grafiek van f?
y
3
2
Oplossing
1 De grafiek is ontstaan uit de grafiek van h(x) = x3.
2 Het punt (0, 0) is verplaatst naar (–3, –2), dus het
functievoorschrift van f heeft de vorm f(x) = a(x + 3)3 – 2.
3 Het punt (–1, –4) ligt op de grafiek van f, dus
–4 = a(–1 + 3)3 – 2 = 8a – 2.
Hieruit volgt 8a = –2 dus a = – –1
4
1
4 f(x) = – –(x
+ 3)3 – 2.
4
1
–7
–6
–5
–4
–3
–2
–1 O
–1
1
2
3
x
–2
–3
–4
–5
53
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 23 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/102⫺4⫺
Hoofdstuk 2
Test jezelf
Op de computer vind je ook een Test jezelf met andere opdrachten.
y
y
y
3
3
2
2
2
1
1
–2 –1 O
–1
1
1
2
3
4
5
x
–3
–2 –1 O
–1
–5
1
2
3
4
5
6
–4
x
–2
–2
–3
–3
–3
–4
–4
–4
–5
Bovenstaande grafieken zijn door translaties uit standaardgrafieken ontstaan.
Welke standaardgrafieken zijn dit en welke translaties zijn toegepast?
Deze opdracht hoort bij paragraaf 2-1.
T-2
Gegeven zijn de functies f共x兲 ⫽ ⫺3 ⫹ 冪共x ⫹ 2兲, g共x兲 ⫽ 7 ⫺ 共x ⫺ 4兲 3 en
h共x兲 ⫽ 2 ⫹ 2log 共x ⫺ 5兲.
Maak een schets van de grafiek van bovenstaande functies. Geef
randpunten, asymptoten en andere bijzondere punten aan in de grafiek.
Geef bij elke functie aan hoe de grafiek uit een standaardgrafiek kan
ontstaan.
Deze opdracht hoort bij paragraaf 2-2.
b
T-3
a
b
c
d
T-5
a
b
c
54
–2 –1 O
–1
Welke vermenigvuldigingen zijn er nodig
om de grafieken van onderstaande functies
te laten ontstaan uit een standaardgrafiek?
f共x兲 ⫽ 3 ⭈ 2log 共x兲
g共x兲 ⫽ 0,4x 2
h共x兲 ⫽ 7冪共x兲
k共x兲 ⫽ ⫺2 x
Deze opdracht hoort bij paragaaf 2-3.
1
2
3
–2
T-1
a
–3
T-4
a
b
c
Welke vermenigvuldigingen zijn er nodig
om de grafieken van onderstaande functies
te laten ontstaan uit een standaardgrafiek?
r共x兲 ⫽ 冪 ⫺ 2x
s共x兲 ⫽ log x ⫹ log 8
r共x兲 ⫽ 2
3x
Deze opdracht hoort bij paragaaf 2-4.
De uitwijking van de slinger hiernaast wordt gegeven door de
formule u ⫽ sin t. Hierbij is u de uitwijking in cm ten
opzichte van een verticale lijn en t is de tijd in seconden.
Een tweede slinger heeft dezelfde slingertijd maar een twee
maal zo grote uitwijking. Welke formule past bij de
uitwijking van deze slinger?
Van een derde slinger is de maximale uitwijking gelijk aan
die van de eerste slinger maar de slingertijd is twee maal zo
groot. Geef een formule bij de uitwijking van deze slinger.
Teken de grafieken van de uitwijkingen van de drie slingers
in één figuur.
u(t)
4
x
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 24 SESS: 18 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/102⫺4⫺
Hoofdstuk 2
y
y
4
4
3
3
2
2
1
1
–5
T-6a
b
T-7
a
b
c
d
T-8
a
b
c
d
T-9
–4
–3
–2
–1 O
–1
1
2
3
4
5
x
–2
–1 O
–1
–2
–2
–3
–3
–4
–4
1
2
3
4
5
6
7
8
x
Geef aan hoe de getekende grafieken door transformaties uit een
standaardgrafiek kunnen ontstaan.
Stel functievoorschriften op die bij deze grafieken passen.
De grafiek van y ⫽ x 3 wordt 4 naar links en 2 naar beneden verschoven.
Daarna wordt de beeldgrafiek ten opzichte van de x-as vermenigvuldigd
met factor 12 . Zo ontstaat de grafiek van een functie g.
Ga uit van het punt 共0, 0兲. Waarheen wordt dit punt na elke transformatie
verplaatst?
Beantwoord opdracht a ook voor het punt 共1, 1兲.
Teken de grafiek van g.
Geef het functievoorschrift van g.
Op de standaardgrafiek y ⫽ 1 worden de
x
volgende transformaties toegepast. Geef steeds
een functievoorschrift bij de beeldgrafiek.
De translatie van 1 naar rechts gevolgd door de
vermenigvuldiging ten opzichte van de y-as met
factor 2.
De vermenigvuldiging ten opzichte van de y-as
met factor 2 gevolgd door de translatie van 1
naar rechts.
De translatie van 4 naar boven gevolgd door de
vermenigvuldiging ten opzichte van de x-as met
factor 2.
De vermenigvuldiging ten opzichte van de x-as
met factor 2 gevolgd door de translatie van 4
naar boven.
De grafiek van f共x兲 ⫽ 2x ⫺ 5 is ontstaan uit de grafiek
x⫺3
van y ⫽ 1
x
Welke transformaties zijn daarbij gebruikt?
55
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 21 SESS: 30 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/104⫺4⫺
Hoofdstuk 4
Samenvatting
Riemann-som en integraal
Met een Riemann-som benader je de oppervlakte van het gebied tussen een
grafiek en de x-as op het interval 关a,b兴 door dat gebied in rechthoekjes te
verdelen en de oppervlakten daarvan op te tellen. Hoe groter het aantal
rechthoekjes des te nauwkeuriger wordt de benadering.
b
De exacte oppervlakte bereken je met de integraal 兰 f共x兲dx.
a
b
Het berekenen van 兰 f共x兲dx heet integreren.
a
Primitieve functie
De functie F is een primitieve van de functie f als geldt F⬘共x兲 ⫽ f共x兲.
Hoofdstelling van de integraalrekening
b
兰 f共x兲dx ⫽ F共b兲 ⫺ F共a兲
a
Je kunt met behulp van een Riemann-som een oppervlakte
benaderen
Verdeel het integratie-interval in een aantal deelintervallen en kies op elk
deelinterval een functiewaarde. Een Riemann-som bereken je door steeds
de gekozen functiewaarde met de lengte van het deelinterval te
vermenigvuldigen en alle uitkomsten op te tellen.
Voorbeeld
1 3
Benader de oppervlakte tussen de grafiek van f(x) = –x
en de x-as
4
op het interval [0, 3] met het gemiddelde van een ondersom en een
bovensom.
Gebruik zes deelintervallen van gelijke breedte.
y
6
4
2
O
116
1
2
1
1
12
1
2 22
3
1
32
x
Oplossing
De ondersom is gelijk aan
1 3
–(0
· 0,5 + 0,53 · 0,5 + 13 · 0,5 + 1,53 · 0,5 + 23 · 0,5 + 2,53 · 0,5)≈
4
3,52.
De bovensom is gelijk aan:
1
3 · 0,5 + 13 · 0,5 + 1,53 · 0,5 + 23 · 0,5 + 2,53 · 0,5 + 33 · 0,5)≈
–(0,5
4
6,89.
Het gemiddelde van onder- en bovensom ≈ 5,21.
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 22 SESS: 28 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/104⫺4⫺
Hoofdstuk 4
Je kunt een machtsfunctie primitiveren
Gebruik hierbij de volgende regel:
Als f共x兲 ⫽ x a dan is F共x兲 ⫽ 1 ⭈ x a ⫹ 1 ⫹ C met a ⫽ 1.
a⫹1
Voorbeeld
Geef de primitieve functies van f(x) = 33
4x
Oplossing
Je kunt schrijven
3 –3
f(x) = –x
4
De primitieven zijn dan de functies
3
F(x) = –4 · 3
–3+1
Je kunt functies van het type k共x兲 ⫽ 共f共x兲兲 a primitiveren,
als f een lineaire functie is
Probeer als primitieve functie K共x兲 ⫽ p ⭈ 共f共x兲兲 a ⫹ 1 en
bereken K⬘共x兲.
Bereken vervolgens de waarde van p waarvoor geldt
K⬘共x兲 ⫽ k共x兲.
x –3+1 + C = –32 + C.
8x
Voorbeeld
Geef de primitieve functies van f(x) = (3 – 4x)5.
Oplossing
Probeer als primitieve F(x) = a(3 – 4x)6.
F'(x) = a · 6(3 – 4x)5 · –4 = –24 a · (3 – 4x)5.
Daaruit volgt dat –24a = 1 , dus a = – 1
24
De primitieven zijn de functies
F(x) = – 1 (3– 4x)6 + C.
24
Je kunt de oppervlakte tussen grafieken exact
berekenen
Maak een schets van de grafieken en geef het gebied aan waarvan je de
oppervlakte moet berekenen.
Bereken exact de snijpunten van de grafieken en stel een integraal op.
Let goed op welke grafiek boven ligt.
Voorbeeld
y
Bereken de oppervlakte van het gebied dat wordt ingesloten door de
grafieken van f(x) = –x2 en g(x) = x2 – 4x.
g
Oplossing
De snijpunten van beide grafieken vind je door de vergelijking
–x2 = x2 –4x op te lossen. Je vindt de punten (0, 0) en (2, –4).
De oppervlakte van het gebied is gelijk aan
2
2
0
0
2
2 3
2
∫(–x2 –(x2 –4x))dx = ∫(4x – 2x2)dx = [2x2 – –x
] = 2–.
3
0
O
x
f
3
117
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 23 SESS: 30 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/104⫺4⫺
Hoofdstuk 4
Test jezelf
Op de computer vind je ook een Test jezelf met andere opdrachten.
T-1
1 2
Gegeven is de functie f共x兲 ⫽ ⫺ 10
x ⫹ 2x ⫹ 1 met domein 关0, 10兴.
Hieronder staat de grafiek.
y
2
1
1
O
a
b
c
d
e
T-2
2
10
x
Bereken de ondersom en de bovensom die in de figuur zijn aangegeven.
Bereken opnieuw onder- en bovensom, neem nu intervallen met lengte 1.
Is het verschil tussen onder- en bovensom nu groter of kleiner dan bij
opdracht a? Waarom kon je deze uitkomst verwachten?
Neem nu intervallen met lengte 0,2. Leg uit dat het midden van het k-de
deelinterval het getal 0,1 ⭈ 共2k ⫺ 1兲 is.
Stel de Riemann-som op die bij opdracht d hoort en bereken die som met
je rekenmachine.
Deze opdracht hoort bij paragraaf 4-1.
Bereken de volgende integralen met behulp van je rekenmachine. Schets daarna
de grafiek van de integrand en arceer het bij de integraal behorende gebied.
4
a
b
兰 共6冪x ⫺ 2x兲dx
1
⫺1
T-3
a
b
118
冉
冊
⫹ 8 dx
兰 ⫺2
x3 x2
Deze opdracht hoort bij paragraaf 4-2.
⫺3
Gegeven zijn de functies f共x兲 ⫽ x en g共x兲 ⫽ 冪x ⫹ 2.
De grafieken van beide functies en de x-as sluiten een gebied in.
Geef met één of meer integralen de oppervlakte van dit gebied weer en
benader de oppervlakte met je rekenmachine. Rond af op twee decimalen.
Bereken de exacte oppervlakte van het gebied dat wordt ingesloten door de
grafieken van f en g en de y-as.
Deze opdracht hoort bij paragraaf 4-3.
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 24 SESS: 37 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/104⫺4⫺
Hoofdstuk 4
T-4
a
b
Geef primitieven van de volgende functies.
f共x兲 ⫽ 2x ⫺ 3x 2 ⫹ 4x 3
3
5
f共x兲 ⫽ x冪x ⫹ 3x 2冪x ⫺ 2
冪x
c
d
f共x兲 ⫽ ⫺2x 2 ⫹ 1 3
3x
3
x
2x
⫺
3
⫹
f共x兲 ⫽
x5
Deze opdracht hoort bij paragraaf 4-4.
T-5
y
Gegeven is de functie f共x兲 ⫽ 3冪x ⫹ 4.
Hiernaast zijn de grafiek van f en de lijn x ⫽ a getekend.
De grafiek van f en de beide assen sluiten links van de y-as
een gebied A in.
De grafiek van f en de beide assen en de lijn x ⫽ a sluiten
rechts van de y-as een gebied B in.
Bereken a als gegeven is dat de oppervlakten van beide
gebieden even groot zijn Rond je antwoord af op twee
decimalen.
Deze opdracht hoort bij paragraaf 4-5.
6
–4
T-6
Gegeven zijn de functies f共x兲 ⫽ 18 x 2 ⫹ 2 en g共x兲 ⫽ 4冪x ⫺ 4.
Beide functies hebben als domein 关0, 4兴.
De grafieken van beide functies raken elkaar in het punt 共4, 4兲.
Bereken exact de oppervlakte van het gebied dat door beide
grafieken en de y-as wordt ingesloten:
–2
O
x=a
x
y
4
(4, 4)
f
g
2
O
1
2
3
4
x
–2
–4
T-7
a
b
c
6 en g共x兲 ⫽ 2
Gegeven zijn de functies f共x兲 ⫽ 8x ⫺
x3
x2
Bereken de coördinaten van het snijpunt van beide grafieken.
Bereken de oppervlakte van het gebied dat wordt ingesloten door beide
grafieken en de lijn x ⫽ 4.
Het gebied begrensd door de lijnen x ⫽ 1, x ⫽ a met a ⬎ 1, de grafiek van f
en de x-as wordt door de grafiek van g verdeeld in twee delen met gelijke
oppervlakte.
Bereken a.
119
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 15 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/105⫺4⫺
Hoofdstuk 5
Samenvatting
Meetkundige plaats
De verzameling van alle punten met dezelfde eigenschap heet een
meetkundige plaats.
Middelloodlijn, deellijn, middenparallel, koorde
De middelloodlijn van lijnstuk AB is de lijn die loodrecht op AB staat en
door het midden van AB gaat. Punten op de middelloodlijn hebben gelijke
afstand tot A en B.
Een deellijn of bissectrice van een hoek is de halve lijn die een hoek
middendoor deelt. Punten op de deellijn van een hoek hebben gelijke
afstand tot de benen van die hoek.
Een middenparallel van twee evenwijdige lijnen l en m is de lijn die
evenwijdig loopt aan l en m en die op gelijke afstand van l en m ligt.
Een koorde is het verbindingslijnstuk van twee punten op een cirkel.
Je kunt de omgeschreven en ingeschreven cirkel van een driehoek
tekenen
Het snijpunt van de middelloodlijnen van een driehoek is het
middelpunt van de omgeschreven driehoek.
Het snijpunt van de deellijnen van de hoeken van een
driehoek is het middelpunt van de ingeschreven driehoek.
C
C
Q
R
E
M
N
A
D
B
A
150
P
B
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 16 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/105⫺4⫺
Hoofdstuk 5
Je kunt de eigenschap van een meetkundige plaats bewijzen
F ligt op l ⇔ F heeft eigenschap X
Je bewijst beide implicaties apart:
⬎ F ligt op l ⇒ F heeft eigenschap X
⬎ F heeft eigenschap X ⇒ F ligt op l
Voorbeeld
Gegeven is ABP.
Te bewijzen:
P ligt op de middelloodlijn van AB ⇔
P
ABP is gelijkbenig.
Oplossing
Bewijs:
P ligt op de middelloodlijn van AB ⇒ AP = BP ⇒ ABP is gelijkbenig.
ABP is gelijkbenig ⇒ AP = BP ⇒ P ligt op de middelloodlijn van AB.
A
B
Je kunt punten construeren die aan twee of meer voorwaarden
voldoen
Omschrijf welke meetkundige plaats bij elke voorwaarde
hoort en teken deze meetkundige plaatsen.
Voorbeeld
Gegeven de lijnen k, l en m.
Construeer de middelpunten van de cirkels c die k en l
raken en waarvan het middelpunt M op afstand 1 cm van
de lijn m ligt.
Oplossing
1 d(M, k) = d(M, l)
d(M, m) = 1 cm.
2 M ligt op een deellijn d van k en l.
M ligt op een lijn n ⁄⁄ m met d(n, m) = 1 cm.
3 Teken de deellijnen d1 en d2 en de lijnen n1 en n2.
4 Geef vier mogelijke punten voor M aan.
n2
n1
M1
d2
M4
k
M3
d1
l
M2
m
151
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 17 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/105⫺4⫺
Hoofdstuk 5
Test jezelf
Op de computer vind je ook een Test jezelf met andere opdrachten.
T-1
Bewijs de volgende stelling:
Als twee cirkels elkaar snijden in twee punten
P en Q dan is de lijn door de twee
middelpunten de middelloodlijn van de
gemeenschappelijke koorde PQ.
Deze opdracht hoort bij paragraaf 5-1.
P
m
M1
M2
Q
T-2
a
b
T-3
a
b
c
d
Gegeven is een driehoek ABC, de deellijn van ⬔A, en de
deellijnen van de buitenhoeken van ⬔B en ⬔C.
Bewijs dat deze drie deellijnen door één punt gaan.
Er is een cirkel 共M, r兲 die raakt aan AB en aan de verlengden
van de zijden CA en CB. Leg uit hoe je punt M kunt construeren.
Deze opdracht hoort bij paragraaf 5-2.
Gegeven zijn twee punten A en P.
Teken een lijn l door A en teken vervolgens het
beeldpunt P⬘ van P bij spiegeling in lijn l.
Teken een andere lijn m door A en teken het
beeldpunt van P bij spiegeling in lijn m.
Onderzoek wat de meetkundige plaats is van de
beeldpunten van P bij spiegeling in lijnen door
het punt A.
Bewijs je vermoeden uit opdracht c.
Deze opdracht hoort bij paragraaf 5-3.
T-4
Gegeven zijn twee snijdende lijnen p en q.
Construeer alle cirkels met straal 2 die de lijnen
p en q raken.
Deze opdracht hoort bij paragraaf 5-4.
T-5
Hiernaast staat een deel van een cirkel
getekend. Je gaat het middelpunt construeren.
Schrijf op wat je weet van de ligging van het
middelpunt van een cirkel.
Construeer het middelpunt.
a
b
152
I
A
P
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 18 SESS: 18 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/105⫺4⫺
Hoofdstuk 5
T-6
a
b
c
T-7
a
b
c
T-8
a
b
T-9
Stelling:
In een gelijkbenige driehoek is de bissectrice van de
buitenhoek van de tophoek evenwijdig met de basis.
Maak een analysefiguur en bewijs deze stelling.
Formuleer het omgekeerde van deze stelling als een
implicatie.
Ga na of deze omgekeerde stelling waar is.
Zo ja, geef hiervoor dan het bewijs. Zo nee, licht je antwoord
toe met een voorbeeld.
Gegeven is driehoek ABC met bissectrice AD. In deze
driehoek geldt |AD| ⫽ |AB| ⫽ |CD|.
Teken een analysefiguur en geef daarin gelijke hoeken en
gelijke lengten aan.
Door de gegevens ligt de vorm van de driehoek en dus de
grootte van de hoeken ⬔A, ⬔B en ⬔C volledig vast.
Zoek verschillende verbanden tussen deze hoeken.
Bereken de grootte van deze drie hoeken.
Teken twee snijdende lijnen l en m en noem het snijpunt S.
Construeer vier cirkels met gelijke stralen die de lijnen l en m
raken.
De middelpunten van de cirkels uit opdracht a zijn M 1, M 2,
M 3 en M 4. Hoe moet je l en m tekenen zodat deze
middelpunten op een cirkel liggen met middelpunt S?
Geef hiervoor een bewijs.
P
De lijnen m en n zijn evenwijdig. Lijn l is de middenparallel
van de lijnen m en n. Punt P ligt op n en punt Q ligt op m.
Bewijs dat het snijpunt van de deellijnen van de hoeken P en
Q op de lijn l ligt.
l
Q
?
T-10a
b
c
n
m
Heeft elk parallellogram een omgeschreven cirkel?
Wat weet je van een parallellogram als dit een omgeschreven
cirkel heeft?
Beschrijf hoe de verzameling punten met een vaste afstand
tot een lijnstuk AB er uit ziet.
153
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 19 SESS: 21 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/106⫺4⫺
Hoofdstuk 6
Samenvatting
C
Middelpuntshoeken, omtrekshoeken en bogen
Een middelpuntshoek is een hoek waarvan het hoekpunt op
het middelpunt van de cirkel ligt.
Een omtrekshoek is een hoek waarvan het hoekpunt op de
cirkel ligt en de benen de cirkel snijden of raken.
Een boog is een gedeelte van een cirkel.
M
E
1 DE
∠C = –bg
2
De meetkundige plaats van een constante hoek
De meetkundige plaats van alle punten P waarvoor geldt dat
⬔APB ⫽ ␣ , bestaat uit twee cirkelbogen.
α
B
α
α
A
Koordenvierhoek
Een koordenvierhoek is een vierhoek waarvan de hoekpunten
op een cirkel liggen.
De som van twee overstaande hoeken in een koordenvierhoek
is 180 ⴰ.
Omgekeerd geldt: als de som van twee overstaande hoeken in
een vierhoek 180 ⴰ is, dan is de vierhoek een
koordenvierhoek.
Je kunt beweringen over middelpuntshoeken, omtrekshoeken en
bogen bewijzen
Bij bewijzen over hoeken in cirkels speelt, naast het gelijk zijn van bogen,
de hoekensom van een driehoek vaak een rol.
Voorbeeld
Twee cirkels met middelpunten M en N snijden elkaar in S.
De lijnen NS en MS snijden de cirkels in de punten A
respectievelijk B. Bewijs dat ∠AMS = ∠BNS.
172
A
bg AB = ∠M
Stelling van de omtrekshoek
Elke omtrekshoek is gelijk aan de helft van de bijbehorende
middelpuntshoek.
Oplossing
∠AMS = 180° – 2 · ∠ASM (hoekensom en ⎢MA ⎢= ⎢MS ⎢)
∠BNS = 180° – 2 · ∠BSN (hoekensom en ⎢NB ⎢= ⎢NS ⎢)
∠ASM = ∠BSN (overstaande hoeken)
dus geldt ∠ASM = ∠BNS.
B
D
M
N
A
S
B
α
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 20 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/106⫺4⫺
Hoofdstuk 6
Voorbeeld
In een cirkel met middelpunt M is AB een middellijn en
is BC een raaklijn. AC snijdt de cirkel in D.
Bewijs dat ∠C = ∠E.
C
D
Oplossing
∠C = 90° – ∠BAC = 90° – –12 bg BD
A
M
1 AD = –(bg
1
∠E = –bg
ADB – bg BD) =
2
2
B
–12 (180° – bg BD) = 90° – –12 bg BD
dus ∠C = ∠E.
E
Je kunt nagaan of een vierhoek een koordenvierhoek is
Met behulp van één van de eigenschappen hieronder kun je nagaan of je te
maken hebt met een koordenvierhoek:
> De som van een paar overstaande hoeken is 180 ⴰ.
> De meetkundige plaats van de constante hoek.
> Drie middelloodlijnen van de zijden gaan door één punt.
Voorbeeld
C
In de figuur is I het middelpunt van de ingeschreven cirkel en
J is het middelpunt van een aangeschreven cirkel van ABC.
Te bewijzen: vierhoek AJBI is een koordenvierhoek.
Oplossing
Het middelpunt I is het snijpunt van de bissectrices van
∠BAC en ∠ABC. Het middelpunt J ligt op de bissectrice van
∠C en op de bissectrices van de buitenhoeken van de driehoek
bij A en bij B. Deze bissectrices staan loodrecht op elkaar.
Dus geldt dat ∠IAJ = 90° en ∠IBJ = 90°.
Maar dan is de som van twee overstaande hoeken 180° en
daarmee is AJBI een koordenvierhoek.
××
I
B
A
J
Je kunt nagaan of een meetkundige plaats een cirkelboog is
Als je de stelling van de constante hoek kunt toepassen dan is de
meetkundige plaats een cirkelboog.
Voorbeeld
Vanuit punt A buiten een cirkel snijdt een lijn l de cirkel in de
punten B en C. Het midden van BC is P. Welke baan beschrijft
P als l om A draait?
Oplossing
Omdat P het midden is van koorde BC geldt ∠APM = 90°.
Volgens de stelling van Thales geldt dat P op de cirkel met
middenlijn AM ligt.
A
C
P
B
M
173
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 21 SESS: 17 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/106⫺4⫺
Hoofdstuk 6
Test jezelf
Op de computer vind je ook een Test jezelf met andere opdrachten.
T-1
a
b
c
d
e
T-2
C
In de tekening hiernaast is driehoek ABC gelijkbenig met
⬔C ⫽ 70 ⴰ. De zijde AB is een middellijn van de cirkel met
middelpunt M.
Verklaar met behulp van omtrekshoeken dat bg DB ⫽ 110 ⴰ.
Bereken bg DA en bg DE.
Neem de figuur over en teken ook de lijnstukken MD en ME
en verklaar met behulp van middelpuntshoeken dat bg BE ⫽ 70°.
Neem nu ⬔C ⫽ ␣. Welke eis moet je daarbij aan ␣ stellen?
Druk de hoeken van vierhoek ABED uit in ␣.
Deze opdracht hoort bij paragraaf 6-1.
A
B
M
D
P
Q
E
A
A
E
C
In de figuur zie je driehoek ABC met de omgeschreven cirkel.
De bissectrice van ⬔A snijdt de cirkel in D, de bissectrice
van ⬔B snijdt de cirkel in E. Lijn ED snijdt AC in Q en BC
in P.
Bewijs dat |CP| ⫽ |CQ|.
Deze opdracht hoort bij paragraaf 6-2.
B
70°
D
B
P
P
A
T
D
C
T-3
a
b
174
B
Q
Q
In de figuur snijden twee cirkels elkaar in de
punten P en Q. Een lijn door P snijdt de cirkels
in A en B en een lijn door Q snijdt de cirkels in
C en D. Te bewijzen: AC // BD.
Welke koordenvierhoeken tref je in deze figuur
aan?
Zoek gelijke hoeken en bewijs dat AC // BD.
Deze opdracht hoort bij paragraaf 6-3.
T-4
a
b
c
d
In de figuur is willekeurig op één van de cirkels
een punt T gekozen. De lijnen TA en TB snijden
de andere cirkel in P en Q.
Waarom is ⬔ATB constant?
Teken koorde AQ en leg uit waarom ⬔AQT
constant is.
Bewijs dat ⬔PAQ constant is.
Wat kun je nu zeggen over de lengte van PQ?
Deze opdracht hoort bij paragraaf 6-4.
JOBNAME: 978⫺90⫺01⫺60674⫺9.MW PAGE: 22 SESS: 21 OUTPUT: Tue May 13 13:59:06 2008
/een/noordhoff/301/900/106⫺4⫺
Hoofdstuk 6
T-5
a
b
c
d
T-6
De cirkels c en k snijden elkaar in de punten A en B.
Punt Q ligt op cirkel c. De lijn QA snijdt cirkel k behalve in
A ook in punt P. De lijn PB snijdt cirkel c behalve in B ook
in punt R. Lijn t is de raaklijn in punt P aan cirkel k.
Te bewijzen: t // QR.
Er komen cirkels voor: kun je koordenvierhoeken of gelijke
omtrekshoeken ontdekken?
Aan welke hoek zou ⬔TPA gelijk moeten zijn als de twee
lijnen evenwijdig zijn?
Beide hoeken moet je aan elkaar zien te koppelen. Welke
hoek bij A of B zou als tussenschakel kunnen dienen?
Geef het bewijs dat t // QR.
Deze opdracht hoort bij paragraaf 6-5.
t
T
P
k
A
Q
B
c
R
P
In de figuur zijn de koorden PA en PB even lang. Ook de
koorden PC en PD zijn even lang.
Bewijs dat de lijnen AB en CD evenwijdig zijn.
B
A
T-7
Van een driehoek ABC is zijde AB even lang als de straal van
de omgeschreven cirkel. Hoe groot is hoek C?
D
C
T-8
C
In de figuur hiernaast is de cirkel met middelpunt M en straal
R de omgeschreven cirkel van driehoek ABC.
Bewijs dat R ⫽ a .
2 sin ␣
b
a
M
A
α
B
c
D
T-9
a
b
c
d
Q
In de figuur zie je koordenvierhoek ABCD waarvan de
verlengde zijden elkaar snijden in de punten P en Q.
De bissectrices van ⬔BPC en ⬔DQC snijden elkaar in
punt S.
Bewijs dat ⬔CPQ ⫹ ⬔CQP ⫽ ⬔BAD.
Bewijs dat ⬔BPS ⫽ 90⬚ ⫺ 12 共⬔BAD ⫹ ⬔ADC兲.
Druk ook ⬔CQS uit in de hoeken van vierhoek ABCD.
Bewijs dat de bissectrices PS en QS elkaar loodrecht snijden.
D
C
S
A
P
B
175