Newton VWO - natuurkunde

Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
1
Polsstokhoogspringen (vwo 1985)
Tegenwoordig maakt men bij het polsstokhoogspringen gebruik van een stok gemaakt van
glasfiber. De 4,80 m lange stok is cilindervormig en hol. De buitendiameter is 4,0 cm, de
binnendiameter is 3,6 cm. De massa van de stok is 2,3 kg.
a
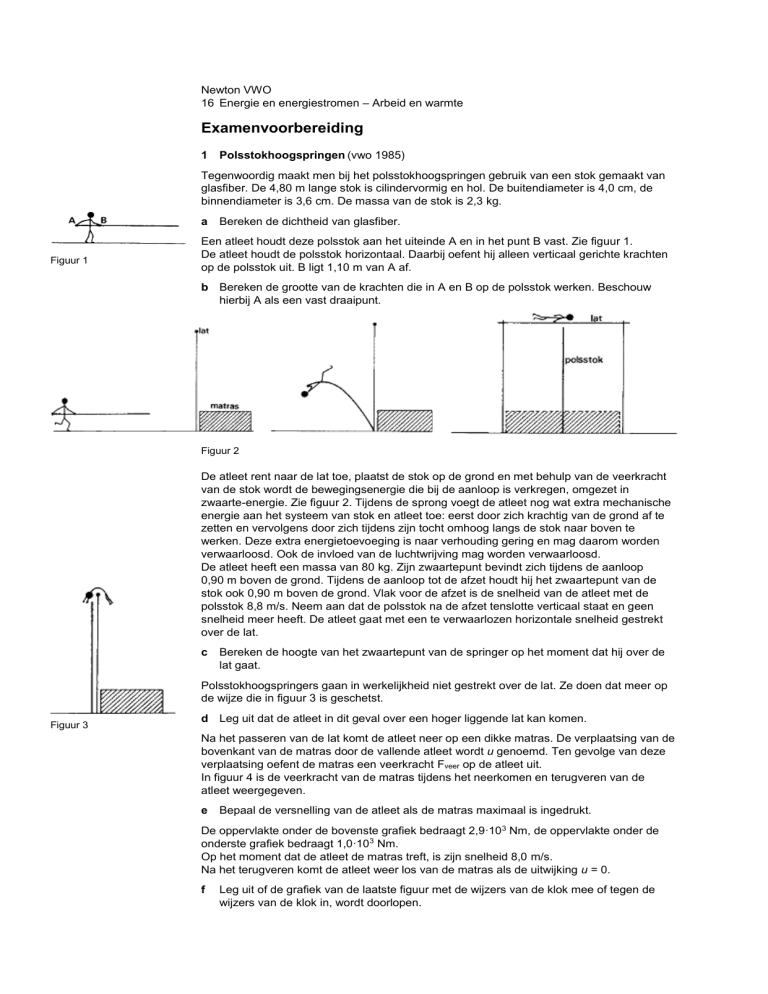
Figuur 1
Bereken de dichtheid van glasfiber.
Een atleet houdt deze polsstok aan het uiteinde A en in het punt B vast. Zie figuur 1.
De atleet houdt de polsstok horizontaal. Daarbij oefent hij alleen verticaal gerichte krachten
op de polsstok uit. B ligt 1,10 m van A af.
b Bereken de grootte van de krachten die in A en B op de polsstok werken. Beschouw
hierbij A als een vast draaipunt.
Figuur 2
De atleet rent naar de lat toe, plaatst de stok op de grond en met behulp van de veerkracht
van de stok wordt de bewegingsenergie die bij de aanloop is verkregen, omgezet in
zwaarte-energie. Zie figuur 2. Tijdens de sprong voegt de atleet nog wat extra mechanische
energie aan het systeem van stok en atleet toe: eerst door zich krachtig van de grond af te
zetten en vervolgens door zich tijdens zijn tocht omhoog langs de stok naar boven te
werken. Deze extra energietoevoeging is naar verhouding gering en mag daarom worden
verwaarloosd. Ook de invloed van de luchtwrijving mag worden verwaarloosd.
De atleet heeft een massa van 80 kg. Zijn zwaartepunt bevindt zich tijdens de aanloop
0,90 m boven de grond. Tijdens de aanloop tot de afzet houdt hij het zwaartepunt van de
stok ook 0,90 m boven de grond. Vlak voor de afzet is de snelheid van de atleet met de
polsstok 8,8 m/s. Neem aan dat de polsstok na de afzet tenslotte verticaal staat en geen
snelheid meer heeft. De atleet gaat met een te verwaarlozen horizontale snelheid gestrekt
over de lat.
c
Bereken de hoogte van het zwaartepunt van de springer op het moment dat hij over de
lat gaat.
Polsstokhoogspringers gaan in werkelijkheid niet gestrekt over de lat. Ze doen dat meer op
de wijze die in figuur 3 is geschetst.
Figuur 3
d Leg uit dat de atleet in dit geval over een hoger liggende lat kan komen.
Na het passeren van de lat komt de atleet neer op een dikke matras. De verplaatsing van de
bovenkant van de matras door de vallende atleet wordt u genoemd. Ten gevolge van deze
verplaatsing oefent de matras een veerkracht Fveer op de atleet uit.
In figuur 4 is de veerkracht van de matras tijdens het neerkomen en terugveren van de
atleet weergegeven.
e
Bepaal de versnelling van de atleet als de matras maximaal is ingedrukt.
De oppervlakte onder de bovenste grafiek bedraagt 2,9·10 3 Nm, de oppervlakte onder de
onderste grafiek bedraagt 1,0·103 Nm.
Op het moment dat de atleet de matras treft, is zijn snelheid 8,0 m/s.
Na het terugveren komt de atleet weer los van de matras als de uitwijking u = 0.
f
Leg uit of de grafiek van de laatste figuur met de wijzers van de klok mee of tegen de
wijzers van de klok in, wordt doorlopen.
g Bereken de snelheid van de atleet op het moment dat hij weer los komt van de matras.
Figuur 4
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
2
Duikplank (vwo 1986)
Een meisje met een massa van 45 kg staat op het uiteinde C van een duikplank. Zie figuur
1. De duikplank kan draaien om as A en ligt in B op een steunpunt. De massa van de plank
wordt in dit vraagstuk verwaarloosd. De afstand tussen as A en steunpunt B is 1,6 m. De
afstand tussen as A en uiteinde C is 4,8 m.
a
Bereken de grootte van de kracht die door het steunpunt B op de plank wordt
uitgeoefend als het meisje in C op de duikplank staat.
Figuur 1
Als het meisje van 45 kg in C op de duikplank staat, is de plank daar 12,9 cm doorgezakt.
b Bereken met behulp van deze gegevens de veerconstante (krachtconstante) van de
duikplank voor een belasting in punt C.
Het meisje brengt zichzelf in een verticale trilling door met haar benen afwisselend buig- en
strekbewegingen te maken. Na een poosje stopt zij hiermee. Zij voert dan in verticale
richting een harmonische trilling uit, waarbij zij in contact blijft met de plank. In figuur 2 is
haar snelheid v als functie van de tijd t weergegeven.
Figuur 2
Het tijdstip t = 0 s correspondeert met haar laagste positie.
c
Bepaal met behulp van dit v,t-diagram de amplitude van deze trilling.
Het meisje vergroot de amplitude van de trilling. Bij de periodieke beweging die zij daarna
uitvoert, komt zij tijdens elke periode enige tijd los van de duikplank. De periodieke
beweging van het meisje bestaat dus uit twee gedeelten: een harmonische trilling zo lang zij
in contact is met de plank en een verticale worp als zij los is van de plank.
Op een bepaald moment, we noemen dit t = 0 s, is het meisje in het laagste punt. In figuur 3
is van haar beweging een gedeelte van het v,t-diagram weergegeven. Dit v,t-diagram geldt
voor elk punt van het lichaam van het meisje.
d Leg met behulp van figuur 3 uit op welk(e) tijdstip(pen) tussen 0 en 1 s het meisje zich in
het hoogste punt bevindt.
e
Tussen welke tijdstippen in het interval van 0 tot 1 s is het meisje los van de plank? Licht
het antwoord toe.
f
Bepaal met behulp van figuur 3 de versnelling van het meisje op t = 0 s.
g Teken in figuur 3 een diagram waarin de versnelling van het zwaartepunt van het meisje
wordt uitgezet tegen de tijd tussen 0 en 1 s.
Figuur 3
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
3
Schommelbeest (vwo 1999)
In stadsparken tref je vaak 'schommelbeesten' aan. Schommelbeesten zijn 'beestachtige'
constructies die op een stugge veer in de grond bevestigd zijn. Kinderen kunnen hier leuk
op schommelen. Een dergelijk schommelbeest wordt een eindje uit zijn evenwichtsstand
getrokken en vervolgens losgelaten. Zie figuur 1.
Figuur 1
Van de beweging van het zwaartepunt is een u,t-diagram geregistreerd met behulp van een
plaatssensor. Vervolgens is aan de hand van dit diagram de versnelling bepaald voor
verschillende waarden van de uitwijking van het zwaartepunt. De beweging blijkt een
harmonische trilling te zijn. In figuur 2 is in grafiek A de versnelling a uitgezet tegen de
uitwijking u.
Figuur 2
Figuur 3
De grafieken B, C en D kunnen geen betrekking hebben op een harmonische trilling.
a
Geef een kenmerk van een harmonische trilling en leg met behulp van dat kenmerk uit
waarom ieder van de grafieken B, C en D niet bij een harmonische trilling horen.
Grafiek A is in figuur 3 weergegeven.
b Bepaal de schommelfrequentie met behulp van figuur 3 in twee significante cijfers. (Hint:
leid eerst een relatie af tussen a(t), u(t) en f voor een harmonische trilling.)
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
4
Pompen (vwo 2000)
De polder waarin Oostelijk en Zuidelijk Flevoland liggen, is helemaal omgeven door water.
Met behulp van pompen wordt in deze polder de waterstand op een constant peil gehouden.
De polder heeft een oppervlakte van 970 km2. Het water uit de polder moet 5,16 m omhoog
worden gepompt naar de omliggende wateren.
Zie de schematische dwarsdoorsnede in figuur 1.
Figuur 1
Alle pompen samen pompen per minuut 8,0·10 3 m3 water weg uit de polder.
De hoeveelheid weg te pompen water hangt onder meer af van de hoeveelheid neerslag en
van de hoeveelheid water die verdampt. Bovendien stroomt kwelwater de polder in.
Dit is water dat via de ondergrond en door de dijken de polder binnenloopt.
In een jaar valt op het totale grondoppervlak 730 mm regenwater, waarvan 610 mm
verdampt. De hoeveelheid kwelwater bedraagt voor de gehele polderoppervlakte 600 mm
per jaar.
a
Bereken hoeveel uren per jaar de pompen samen in bedrijf moeten zijn.
Enkele pompen worden aangedreven door een elektromotor. Als de elektromotor in werking
is, wekt hij een inductiespanning op die tegengesteld is aan de bronspanning.
b Leg aan de hand van de werking van een elektromotor uit waarom hij een
inductiespanning opwekt.
De elektromotor is aangesloten op een bron met een (effectieve) spanning van 3,00 kV.
Als de pomp normaal functioneert, neemt de motor een stroom af van 220 A. Hij is dan in
staat om per minuut 540 m3 water uit de polder naar de omliggende wateren omhoog te
pompen.
Het rendement van de pomp wordt gedefinieerd als het percentage van het door de
spanningsbron geleverde vermogen dat wordt gebruikt om water omhoog te pompen.
c
Bereken dit rendement als de pomp normaal functioneert.
De elektrische pompen zijn in 1991 geautomatiseerd en aangesloten op een automatisch
peilsysteem. Dit peilsysteem omvat diverse sensoren, die hun signalen naar een centrale
computer in Lelystad sturen. Afhankelijk van deze informatie schakelt de computer de
elektrische pompen in, uit, of geeft opdracht water de polder binnen te laten.
d Leg uit of dit peilsysteem een meetsysteem, een stuursysteem of een regelsysteem is.
Figuur 2
Als sensor wordt een drukmeter gebruikt die in een sloot in de polder wordt geplaatst.
De sensor S wordt onder water op een vaste hoogte ten opzichte van de bodem bevestigd.
Zie figuur 2.
De druk die deze sensor meet is de som van de atmosferische druk en de druk van de
waterkolom boven de sensor. Om te corrigeren voor de atmosferische druk wordt een vaste
waarde afgetrokken van de druk die S meet. Voor deze vaste waarde wordt de gemiddelde
atmosferische druk genomen. Dit heeft tot gevolg dat bij het passeren van een depressie
(lagedrukgebied) de waterstand in de polder op een verkeerd peil wordt gebracht.
e
Leg uit of tijdens het passeren van een depressie de waterstand in de polder op een te
hoog peil of op een te laag peil wordt gebracht.
Er kan worden gekozen uit twee typen sensoren. Type 1 heeft een bereik vanaf 0 Pa en kan
bij de gemiddelde atmosferische druk van 1,0·105 Pa meten tot een waterdiepte van
400 cm. Type II heeft een bereik vanaf 1,0·105 Pa en kan bij de gemiddelde atmosferische
druk meten tot een waterdiepte van 900 cm. Een laagje water met een hoogte van 1,0 cm
veroorzaakt een druk van 98 Pa.
Het uitgangssignaal van beide sensoren varieert tussen 0 V en 5,0 V. Beide typen sensoren
zijn lineair.
f
Beredeneer met behulp van een berekening welk type sensor de grootste gevoeligheid
heeft.
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
5
Buitenboordmotor (vwo 2003)
De boot in figuur 1 heeft een lengte van 6,5 m.
Figuur 1
Op het negatief is de afbeelding van de boot 21 mm lang. De foto werd gemaakt met een
lens met een brandpuntsafstand van 80 mm.
a
Bereken de afstand tussen de boot en de fotograaf toen de foto gemaakt werd.
De boot heeft een constante snelheid van 8,5 m/s. Het fototoestel bewoog niet tijdens het
nemen van de foto. De fotograaf weet niet meer met welke sluitertijd de foto is gemaakt.
Omdat hij op de foto geen noemenswaardige bewegingsonscherpte van de armen van de
stuurman ziet, denkt hij dat de sluitertijd niet groter was dan één zestigste seconde.
b Leg met behulp van een berekening en op grond van de foto uit of hij daarin gelijk
heeft.
In figuur 2 is het achterste deel van de boot met de buitenboordmotor op schaal
weergegeven.
De schroef van de buitenboordmotor zit aan een lange as, die schuin in het water steekt.
De kracht F die de schroef op het water uitoefent, heeft dezelfde richting als de
schroefas. De voorwaartse kracht op de boot is horizontaal.
Figuur 2
Bij een snelheid van 8,5 m/s levert de buitenboordmotor aan de boot een vermogen van
8,1 kW.
c
Bepaal de grootte van de kracht die de schroef bij deze snelheid op het water
uitoefent.
De wrijvingskracht op de boot neemt toe als de boot sneller vaart. Het rendement van de
energieomzetting in de buitenboordmotor blijft gelijk.
We bekijken de afstand die de boot met één volle benzinetank kan afleggen.
d Beredeneer of deze afstand bij een hoge snelheid kleiner, even groot of groter is dan
bij een lage snelheid.
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
6
Vertical Shot (vwo 2003)
‘Vertical Shot’ is een nieuwe kermisattractie. Aan twee pilaren van 35 meter hoog zijn
elastieken vastgemaakt. Aan deze elastieken hangt een bol waarin twee personen
plaatsnemen. De bol wordt met behulp van een elektromagneet op de grond gehouden,
terwijl de elastieken aangespannen worden. Nadat de personen vastgegespt zijn, wordt
de elektromagneet uitgezet en schiet de bol verticaal omhoog. In figuur 1 zie je een foto
van de bol vlak voor de start. In figuur 2 zie je een foto waarin de bol omhooggeschoten
is.
Figuur 1
Figuur 2
Figuur 3
Vlak voor het loslaten van de bol zijn de elastieken 20 m uitgerekt.
In figuur 3 is de F,u-grafiek van één elastiek getekend.
In figuur 4 is de richting van de kracht getekend die elk elastiek op de bol uitoefent vlak
voor het loslaten. De kracht die beide elastieken samen op de bol uitoefenen bij het
loslaten noemen we F0.
Er geldt: Fn = 9, 8·103 N.
a
Toon dit aan met behulp van figuur 4.
De massa van bol plus passagiers is 250 kg.
b Bereken de versnelling van de bol direct na het loslaten.
In figuur 5 is de grafiek getekend van de kracht die beide elastieken samen op de bol
uitoefenen als functie van de hoogte tot h = 24 m. Op hoogten groter dan 24 m
ondervindt de bol geen krachten meer van de elastieken.
c
Bepaal met behulp van figuur 5 op welke hoogte de snelheid van de bol maximaal is.
Neem daarbij aan dat wrijvingskrachten geen rol spelen.
d Bepaal met behulp van figuur 5 de maximale hoogte die de bol bereikt. Neem daarbij
aan dat alle arbeid die de elastieken op de bol verrichten in het hoogste punt is
omgezet in zwaarte-energie.
Figuur 4
Figuur 5
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
7
Sprinkhaan (vwo 2005)
De figuur hiernaast is een foto van een
speelgoed-sprinkhaan. Onder het lijf van de
sprinkhaan zit een zuignap, die zich op de
ondergrond vastzuigt als je de sprinkhaan
stevig naar beneden drukt.
Wanneer er lucht onder de zuignap komt,
springt de sprinkhaan omhoog doordat zijn
poten als veren werken.
Tessa en Suzanne doen onderzoek aan de
sprinkhaan. Eén van hun onderzoeksvragen
luidt:
“Hoe groot is de snelheid van de sprinkhaan
als de poten loskomen van de ondergrond?”
Om een idee te krijgen van de grootte van deze snelheid, laten zij de sprinkhaan vanaf de
grond omhoogspringen. Zij schatten de hoogte die de sprinkhaan bereikt op 1,0 m.
a
Bereken met welke snelheid de sprinkhaan volgens deze schatting van de grond
loskomt. Ga er daarbij van uit dat de wrijving verwaarloosbaar is.
In figuur 1 zijn twee standen van de sprinkhaan getekend.
Figuur 1
Op t0 komt de zuignap los van de ondergrond. Op t1 komen de poten los van de ondergrond.
Met behulp van een afstandssensor en een computer maakt Tessa een grafiek die de
hoogte van de sprinkhaan weergeeft als functie van de tijd.
De afstandssensor is zó geijkt dat h = 0 hoort bij de situatie op t1. Zie figuur 2.
Figuur 2
b Bepaal de snelheid op t1 met behulp van een raaklijn in figuur 2.
Na t = 0,75 s valt de sprinkhaan omlaag.
c
Ga met behulp van figuur 2 na of de sprinkhaan bij zijn val meetbare luchtwrijving
ondervindt.
Een andere onderzoeksvraag van Tessa en Suzanne luidt:
“Hoeveel procent van de oorspronkelijke veerenergie wordt er omgezet in zwaarteenergie?”
Susanne duwt de sprinkhaan met behulp van een
krachtmeter omlaag. Bij verschillende waarden van de kracht F meet zij de indrukking u van
de sprinkhaan. Zie figuur 3. Als de zuignap zich vastzuigt, is de sprinkhaan 4,0 cm omlaaggeduwd.
Omdat de wrijving tijdens het indrukken verwaarloosbaar is, kan uit de figuur de veerenergie
worden bepaald die in de poten is opgeslagen.
De massa van de sprinkhaan is 6,2 g.
d Bepaal met behulp van figuur 2 en 3 hoeveel procent van de veerenergie tijdens een
sprong wordt omgezet in zwaarte-energie.
Figuur 3
Figuur 4
Bij het naar beneden duwen van de sprinkhaan oefent de tafel op elk van de vier poten een
kracht Ftafel uit. In figuur 4 is deze kracht op één poot getekend.
Aangenomen mag worden dat:
- de totale duwkracht gelijkmatig over de vier poten verdeeld is
- de zwaartekracht verwaarloosbaar is ten opzichte van de duwkracht.
In figuur 4 is de situatie weergegeven bij een totale duwkracht van 6,0 N.
e
Bepaal met behulp van figuur 4 de grootte van Ftafel. Ontbind Ftafel daartoe eerst in
horizontale en in verticale richting.
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
8
Steppen (vwo 2006)
Arie en Bianca wijden hun praktische opdracht aan natuurkundige aspecten van het
steppen. In figuur 1 zie je een foto van de step die zij gebruiken.
Figuur 1
Figuur 2
Arie gaat met zijn rechtervoet op de step staan en zet (periodiek) met zijn linkervoet af.
Tijdens de afzet neemt de snelheid toe. Na de afzet neemt de snelheid weer af ten gevolge
van wrijving. Zie figuur 2. Een deel van deze figuur staat vergroot weergegeven in figuur 3.
Figuur 3
Arie stept een afstand van 200 m. De snelheid verloopt daarbij voortdurend zoals in figuur 2
is weergegeven.
a
Bepaal hoe vaak Arie een afzetbeweging maakt om 200 m af te leggen.
Arie wil uit de grafiek het grootste vermogen bepalen, dat hij op een bepaald tijdstip levert.
Hij gebruikt daarbij de formule:
P = Fafzet·v = m·a·v
b Leg uit dat het met deze formule bepaalde vermogen maximaal is aan het einde van de
afzet.
c
Leg uit dat Arie bij het gebruik van deze formule de wrijvingskracht verwaarloost.
De massa van Arie met de step is 67 kg.
d Bepaal aan de hand van figuur 3 het maximale vermogen dat Arie door het gebruik van
deze formule vindt.
Op de step werkt een rolwrijvingskracht Fw,rol. Op Arie en de step werkt tevens een kracht
ten gevolge van de luchtweerstand Fw,lucht.
Voor de totale wrijvingskracht geldt:
Fw,totaal = Fw,rol + Fw,lucht
De rolwrijvingskracht is onafhankelijk van de snelheid.
De luchtwrijvingskracht is evenredig met v2.
e
Beschrijf hoe Arie en Bianca met gebruikmaking van een krachtmeter de waarde voor de
rolwrijvingskracht kunnen bepalen.
Newton VWO
16 Energie en energiestromen – Arbeid en warmte
Examenvoorbereiding
9
SoloTrek (vwo 2006)
Lees het volgende artikel.
Zelf vliegen met de SoloTrek
Trek Aerospace Sunnyvale (VS) brengt na jaren van
research en testen de SoloTrek op de markt. Met deze
mini-helicopter kunnen mensen zelfstandig het
luchtruim kiezen.
De SoloTrek heeft twee tegen elkaar in draaiende
rotorbladen in een vaste behuizing die naar voren
kunnen kantelen.
De rotorbladen zorgen zowel voor de kracht die nodig
is om op te stijgen als voor de voortstuwing. De
SoloTrek heeft een tank die 47 liter benzine kan
bevatten en de motor heeft een vermogen van 120 pk.
naar: Technisch Weekblad, 17 januari 2003
Tijdens de start draaien de rotorbladen in een horizontaal vlak. Bij deze start wordt de
luchtweerstandskracht verwaarloosd. In verticale richting werken dan twee krachten op de
SoloTrek: de zwaartekracht Fz en de stuwkracht Fstuw.
Veronderstel dat de stuwkracht constant is. De totale massa bedraagt 255 kg. De piloot
bereikt in 4,0 s een hoogte van 5,0 m.
a
Bereken de hiervoor benodigde stuwkracht.
In het artikel wordt een ouderwetse eenheid van vermogen gebruikt, de paardenkracht (pk).
Zie tabel 5 (Binas vijfde druk) of tabel 6 (Binas vierde druk). Er wordt bedoeld dat het
maximale nuttige vermogen dat de motor kan leveren 120 pk bedraagt. Bij dit vermogen
heeft de motor een rendement van 30%.
b Bereken hoe lang je op dit vermogen kunt vliegen als je met een volle tank begint.