PowerPoint-presentatie

EXTRA BLOK 1 ELEKTRA
JPT 2015-16 Co BTn
SPIEKBRIEFJE
Spanning
=
afgegeven energie per lading
Stroom
=
passerende lading per sec
Weerstand
=
stroomstopper
Vermogen
=
afgegeven energie per sec
P
E el
Q
Q
I 
t
U
R
I
U 
E el
Eel Q

.  U .I
t
Q t
Draadweerstand
Serie
Parallel
R
stroom
I A  I B  IC  I
spanning
U AB  U BC  U CD  U tot
l
A
weerstand
R1  R2  R3  Rtot GROTER
stroom
I1  I 2  I 3  I
spanning
U1  U 2  U 3  U
weerstand
1
1
1
1



KLEINER
R1 R2 R3 Rtot
1
DE WEERSTAND VAN EEN LAMP
Hiernaast zie je de U,I-grafiek van een lamp.
De lamp wordt parallel met een weerstand van
10  aangesloten op een batterij van 3,0 V.
C Teken de (U,I)-grafiek van de 10-Ohms
weerstand in deze figuur in .
D Leg met behulp van die figuur uit hoeveel
stroom de batterij bij parallelschakeling levert.
I par  I lamp  I R  0,53  0,30  0,83( A)
Even later wordt de lamp in serie met de weerstand van 10  aangesloten op dezelfde batterij
van 3,0 V.
E Teken in de 2e fig. de (U,I)-karakteristiek
van de weerstand in en bepaal de stroom die de
batterij levert.
I  0,20( A)  U bron  0,5  1,8  2,3(V )
I  0,30
23( A)  U bron  10,,0732,0,343,,00((VV))
2
FIETSLAMP I
Het fietslampje (6V; 50mA) in de
schakeling hiernaast brandt goed.
A Laat zien dat R2 = 40 Ω.
Upar = 12 - 4 = 8 (V)
U2 = 8 - 6 = 2 (V)
R2 
U2
2(V )

 40()
I boven 0,050( A)
B Bereken R1.
I onder 
U par
Ronder

8(V )
 0,025( A)
320()
Itot =Iboven+Ionder=0,050+ 0,025= 0,075 (A)
R1 
U1
4(V )

 53,3()
I tot 0,075( A)
3
FIETSLAMP II
Een lampje (6,0 V; 3,2 A) is met 3 weerstanden in de
combinatieschakeling van hiernaast geschakeld.
R1 = 10 , R2 = 40  en R3 = 60 . De lamp brandt
normaal (dat is dus 6,0 V)
A Bereken de weerstand van de lamp bij 6 V.
Rlamp 
U 6,0V

 1,875  1,9()
I 3,2 A
B Bereken de vervangingsweerstand van de schakeling.
1
1
1
1


 0,109  R par 
 9,2()
R par 11,875 40
0,109
 Rtot  9,2  60  69,2()
C Bepaal de stroomsterkte in R2 en bereken daaruit de
spanning over R2.
40
Ronder 
I onder
Vonder
Rboven  3,37 xRboven 
11,875
I
3,2
 boven 
 0,95( A) 
3,37 3,37
 IRonder  0,95 x 40  38(V )
D Bereken hoeveel elektronen er per seconde door de
lamp gaan als I=3,2 A.
n I
3,2(C / s )
19
 

2
,
0
x
10
(1 / s )
19
t e 1,6 x10 (C )
IV
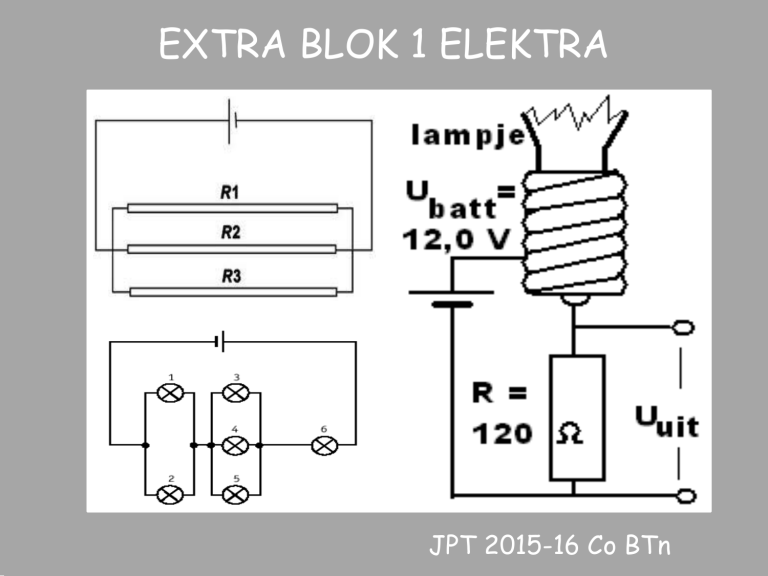
TEMPERATUURSENSOR
Een fietslamp zonder glas wordt als temperatuursensor gebruikt,
de weerstand van het gloeidraadje verandert namelijk als de temperatuur verandert. Bij een temperatuur van 20oC is deze weerstand 10 Ω.
A Leg uit of de weerstand van de gloeidraad groter of kleiner
wordt als de temperatuur stijgt van het draadje stijgt.
Temperatuur hoger  kernen trillen harder  stroom lager  R hoger
e
B Bereken de spanning Uuit bij de temperatuur van 20oC, gebruik
hierbij de gegevens uit nevenstaande figuur.
U  I .R  I bron 
U bron
12

 0,0923( A)
Rtot
120  10
U uit  I .Ruit  0,0923 x120  11,1(V ))
Bij een temperatuur van 4500 oC is de spanning Uuit gelijk aan 6,5 V. Haal de rest van
de gegevens uit het plaatje.
C Bereken de weerstand van de gloeidraad bij deze temperatuur.
U bron  U lamp  U uit  12,0  U lamp  6,5  U lamp  12,0  6,5  5,5(V )
D Geef aan voor welke toepassing deze temperatuursensor geschikt zou zijn.
Super hete dingen  temperatuur vlammen meten
A
ELEKTRICITEIT OP EEN PLANK
Op een houten plank worden vier spijkers in een
vierkant geplaatst en er wordt een draad omheen
geslagen. De zijden zijn 13,8 cm lang, ze hebben
een weerstand van 2,0 Ω en de draaddoorsnede
is 3,1x10-2 mm2.
A Toon met een berekening aan dat de draad
van constantaan is gemaakt.
e
l
AR 3,1x10 8 (m 2 ).2,0()
R  

 0,45x10 6 (m)
A
l
0,138(m)
Rawin sluit op de spijkers A & B een spanningsbron
van 1,2 V aan en hij plaatst een ampèremeter vlak
voor de spanningbron. Hiernaast zie je het schema.
B Bereken de stroom die de meter aanwijst.
R t ot  1,5Ω, want
1
1 1 1 3 4 1
     
Rtot 6 2 6 6 6 1,5
hoofdstroo m uit Ohm : I 
U bron 1,2V

 0,80( A)
Rtot
1,5
VERVOLG ELEKTRICITEIT OP EEN PLANK
Rawin sluit een voltmeter aan tussen A en C.
C Bereken de spanning die de meter aanwijst.
Rboven=6Ω en Ronder=2Ω  Ionder = 3x Iboven
Itot =0,80 (A)
Iboven= ¼ Itot=0,25x0,8 = 0,20(A)
e
= 0,20x4,0 = 0,80(V))
UAC=IxRAC
Rawin sluit nu een stroommeter aan tussen A&C.
D Bereken de stroom die de meter aanwijst.
De ampèremeter heeft weerstand 0 , dus alle
stoom loopt door de meter (niks langs ADC)
Nu is Rtot = 1,0 Ω, want 2 x 2 Ω parallel
Er loopt door A2 0,6 A (1,2V/2Ω), en door A1
1,2 A (beide stromen van 0,6 A tellen op).
B
FRITUURPAN
A
Invullen in regel over vermogen:
B
In schak. 1 is alles parallel aangesloten. Over de lamp staat dan 230 V. Dit is niet juist.
In schak. 2 is alles in serie aangesloten. Het verwarmingselement krijgt minder dan 230
V . Hierdoor zal de stroomsterkte door het verwarmingselement te laag zijn.
C
Voor de weerstand van een draad geldt:
D
De stroom door elke draad is vlgs tabel 1 7,3 A. Beide draden hebben ‘n weerstand van
0,41 Ω. De spanning over beide draden is dan:
Dit is ongeveer het verschil tussen de spanning over de frituurpan wanneer deze
ingeschakeld en uitgeschakeld is. De veronderstelling van Twan is dus juist.
E
De weerstand van de nichroomdraad neemt toe. Aangezien de spanning gelijk blijft zal
vlgs Ohm I = U/R de stroomsterkte I kleiner worden. Als dat zo is, en de spanning gelijk
blijft zal het vermogen P = U.I ook kleiner worden:
C
BRITNED
A
Oneens, in een kring gaat er geen stroomsterkte verloren (stroom gaat nooit verloren)
B
De spanning die verloren gaat in de kabels is 450,0 - 446,6 = 3,4 kV.
De stroomsterkte die de bron levert is:
De geleidbaarheid van de koperen kabel is dan:
C
Je moet rekenen met de soortelijke weerstand.
De weerstand is gelijk aan:
De doorsnede van de gebruikte kabel is dus:
De diameter van de draad volgt dan uit:
VERVOLG BRITNED
D
Massa uit dichtheid:
E
De toegevoegde warmte is gelijk aan:
De temperatuurstijging is dan:
F
Geleidingscoëfficiënt c:
G
H
D
SCHAKELINGENVAN GMr EN BTn
Gerard heeft 2 lampjes, een voorlicht V ( 12 V;6W) en een achterlicht A (6V; 0,3 W).
A Hoeveel stroom trekken de lampjes als ze voluit branden?
I voor 
P 6W

 0,5( A)
U 12V
I achter 
P 0,3W

 0,05( A)
U
6V
B Bereken de grootte van beide weerstanden.
Rvoor
U 12V
 
 24()
I 0,5 A
d
Rachter 
U
6V

 120()
I 0,05 A
Hij heeft een accu van 18 Volt waarop beide lampjes voluit
moeten braden. Hij probeert of dat lukt met nevenstaande
schakeling, waarin beide lampjes parallel geschakeld zijn,
elk met eigen voorschakelweerstanden X en Y om het teveel
aan spanning van de accu op te vangen.
C Bereken de grootte van X en Y.
18 V
V
A
HINT: serieschakeling: stromen gelijk, spanningen tellen op!
D
U 18  12V

 12()
I
0,5 A
Bereken de totale weerstand.
U 18  6V

 240()
I
0,05 A
X 
Y
Rboven  RV  X  24  12  36()
Ronder  R A  Y  120  240  360()
X
Y
ACCU (vervolg)
1
1
1
1
1
10  1 11
360






 Rtot 
 32,7()
Rtot Ronder Rboven 36 360
360
360
11
E Bereken de stroom die de bron levert op twee verschillende manieren:
I bron 
U
18

 0,55( A)
Rtot 32,7
I bron  I1  I 2  0,50  0,05  0,55( A)
n
Bram zegt dat er een veel slimmere schakeling mogelijk is:
18 V
je kan de lampjes in serie schakelen, als je maar een weerstand U parallel schakelt die precies de goede stroom trekt.
F
Teken die schakeling.
G
Bereken de benodigde weerstand U.
RU 
H
U
6
6


 13,3()
I 0,5  0.05 0,45
U
V: 0,50A
Check via de totale weerstand dat er de goede stroom wordt getrokken
1
1
1
1
1
9  1 10
1







 R par  12()
R par RU R A 13,3 120 120 120 12
Rtot  Rvoor  R par  24  12  36()  I tot 
U
18

 0,50( A)
Rtot 36
A: 0,05 A
E
FARADAYMOTOR
A
Soortelijke weerstand formule invullen:
De lengte van de koperdraad is 3 keer zo lang. Dat geeft een 3 keer zo grote weerstand.
De diameter van de koperdraad is 5 keer zo klein, dat geeft een 52 keer zo grote
weerstand. De totale weerstand van de koperdraad is dus 3 * 25 = 75 keer zo groot als
de weerstand van het koperstaafje.
B
Er ontstaat een serieschakeling met de batterij als spanningsbron, met daarop
aangesloten de koperdraden, het koperstaafje en het zoute water.
De totale weerstand is dan:
De stroomsterkte is:
E
FARADAYMOTOR
C
De richting van het magneetveld is aangegeven in
nevenstaande tekening. Aangezien de bovenkant van
het koperstaafje met de pluspool van de batterij
verbonden is, is de stroomrichting naar beneden
gericht. De linkerhandregel geeft dan aan dat de
lorentzkracht het papier uit gericht is. Van bovenaf
gezien draait het staafje met de klok mee.
D
Als het staafje dichter bij koperplaatje K is, zal de totale weerstand kleiner zijn. De
stroom legt dan namelijk minder afstand af in het zoute water. Als de totale weerstand
kleiner is, zal de totale stroomsterkte groter zijn. Hierdoor zal de lorentzkracht ook
groter zijn.
Aangezien de lorentzkracht niet constant is tijdens de baan, zal de baan niet cirkelvormig zijn.
F
SCHRIKDRAAD
A
- De kring: de hoogspanningsbron, de schrikdraad, het dier, de grond en de metalen pen.
- Als er geen contact is met de draad is er geen gesloten kring en loopt er geen stroom.
Daardoor zal er geen elektrische energie verbruikt worden.
B
De doorsnede van de draad is:
De soortelijke weerstand van roestvrij staal staat in Binas en is
Voor de weerstand geldt dan:
C
Het vermogen moet voor beide weerstand bepaald worden. Voor het vermogen geldt:
Voor beide weerstanden kan de spanning afgelezen worden worden, dit geeft:
Dit komt dus voor beide weerstanden overeen met de maximale waarde uit de figuur.
F
SCHRIKDRAAD
D
1. De maximale spanning is nergens hoger dan 8 kV. Aan deze norm wordt voldaan.
2. Een piek duurt 0,3 ms, ruim korter dan de 10 ms die in norm 2 voorgeschreven staat.
Aan deze norm wordt ook voldaan.
3. Voor de stroomsterkte geldt:
Voor de stroomsterkte door de 100 Ω wordt dus niet voldaan aan de norm!
4. De energie in één puls is de oppervlakte onder de grafiek. Elk hokje komt overeen
met 0,025 ms en 5 kW. Dat is een energie van:
Het aantal hokjes is ongeveer 36. De totale energie van 1 puls is dan 36x0,125 = 4,5 J.
Er wordt aan deze norm voldaan.
EINDE
Toen de natuurkunde begon - bij de Grieken, bij de
middeleeuwers en ook nog enigszins bij Galileo en bij
Descartes - ging Natuurkunde over de Natuur: over de
regenboog, over donder en bliksem enz. enz..
Na Newton en vooral na de 19e eeuw is dit niet meer
zo: Natuurkunde gaat over een gestileerde werkelijkheid, die je niet in de natuur maar in de techniek tegen
komt. Dat geldt vooral voor de elektriciteitsleer. Sinds
de elektrificatie van de wereld aan het eind van de 19e
eeuw gaat de natuurkunde over die technische wereld
die we hebben gecreëerd en niet over de verklaring van
elektrische fenomenen in de Natuur.
Die verklaringen hebben we wel, maar ze zijn heel erg
ingewikkeld. Het is ‘n bizarre uithoek voor liefhebbers
geworden, de Natuurkunde van ‘t vrije Veld (Minnaert).